|
Wrapped Cauchy Distribution
In probability theory and directional statistics, a wrapped Cauchy distribution is a wrapped probability distribution that results from the "wrapping" of the Cauchy distribution around the unit circle. The Cauchy distribution is sometimes known as a Lorentzian distribution, and the wrapped Cauchy distribution may sometimes be referred to as a wrapped Lorentzian distribution. The wrapped Cauchy distribution is often found in the field of spectroscopy where it is used to analyze diffraction patterns (e.g. see Fabry–Pérot interferometer). Description The probability density function of the wrapped Cauchy distribution is: : f_(\theta;\mu,\gamma)=\sum_^\infty \frac\qquad -\pi<\theta<\pi where is the scale factor and is the peak position of the "unwrapped" distribution. Expressing the above pdf in terms of the |
Academic Press, Inc
An academy ( Attic Greek: Ἀκαδήμεια; Koine Greek Ἀκαδημία) is an institution of secondary or tertiary higher learning (and generally also research or honorary membership). The name traces back to Plato's school of philosophy, founded approximately 385 BC at Akademia, a sanctuary of Athena, the goddess of wisdom and skill, north of Athens, Greece. Etymology The word comes from the ''Academy'' in ancient Greece, which derives from the Athenian hero, '' Akademos''. Outside the city walls of Athens, the gymnasium was made famous by Plato as a center of learning. The sacred space, dedicated to the goddess of wisdom, Athena, had formerly been an olive grove, hence the expression "the groves of Academe". In these gardens, the philosopher Plato conversed with followers. Plato developed his sessions into a method of teaching philosophy and in 387 BC, established what is known today as the Old Academy. By extension, ''academia'' has come to mean the accumulatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press is the university press of the University of Cambridge. Granted letters patent by Henry VIII of England, King Henry VIII in 1534, it is the oldest university press A university press is an academic publishing house specializing in monographs and scholarly journals. Most are nonprofit organizations and an integral component of a large research university. They publish work that has been reviewed by schola ... in the world. It is also the King's Printer. Cambridge University Press is a department of the University of Cambridge and is both an academic and educational publisher. It became part of Cambridge University Press & Assessment, following a merger with Cambridge Assessment in 2021. With a global sales presence, publishing hubs, and offices in more than 40 Country, countries, it publishes over 50,000 titles by authors from over 100 countries. Its publishing includes more than 380 academic journals, monographs, reference works, school and uni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Springer Publishing
Springer Publishing Company is an American publishing company of academic journals and books, focusing on the fields of nursing, gerontology, psychology, social work, counseling, public health, and rehabilitation (neuropsychology). It was established in 1951 by Bernhard Springer, a great-grandson of Julius Springer, and is based in Midtown Manhattan, New York City. History Springer Publishing Company was founded in 1950 by Bernhard Springer, the Berlin-born great-grandson of Julius Springer, who founded Springer-Verlag (now Springer Science+Business Media). Springer Publishing's first landmark publications included ''Livestock Health Encyclopedia'' by R. Seiden and the 1952 ''Handbook of Cardiology for Nurses''. The company's books soon branched into other fields, including medicine and psychology. Nursing publications grew rapidly in number, as Modell's ''Drugs in Current Use'', a small annual paperback, sold over 150,000 copies over several editions. Solomon Garb's ''Labor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circular Uniform Distribution
In probability theory and directional statistics, a circular uniform distribution is a probability distribution on the unit circle whose density is uniform for all angles. Description Definition The probability density function (pdf) of the circular uniform distribution, e.g. with \theta\in[0,2\pi), is: : f_(\theta)=\frac. Moments with respect to a parametrization We consider the circular variable z=e^ with z=1 at base angle \theta=0. In these terms, the circular moments of the circular uniform distribution are all zero, except for m_0: :\langle z^n\rangle=\delta_n where \delta_n is the Kronecker delta symbol. Descriptive statistics Here the mean angle is undefined, and the length of the mean resultant is zero. : R=, \langle z^n\rangle, =0\, Distribution of the mean The sample mean of a set of ''N'' measurements z_n=e^ drawn from a circular uniform distribution is defined as: : \overline = \frac\sum_^N z_n = \overline+i\overline = \overlinee^ where the a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
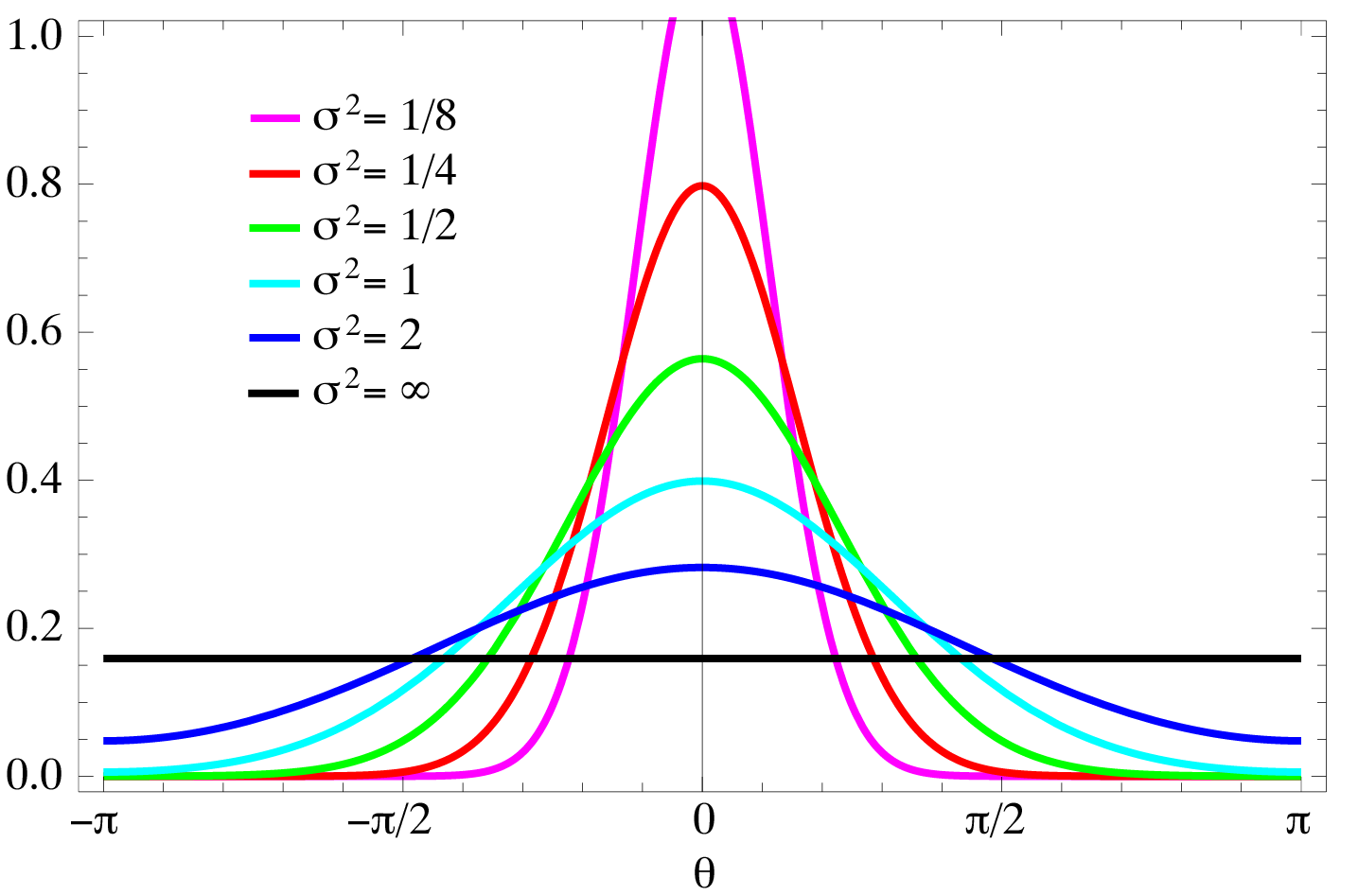
Wrapped Normal Distribution
In probability theory and directional statistics, a wrapped normal distribution is a wrapped probability distribution that results from the "wrapping" of the normal distribution around the unit circle. It finds application in the theory of Brownian motion and is a solution to the heat equation for periodic boundary conditions. It is closely approximated by the von Mises distribution, which, due to its mathematical simplicity and tractability, is the most commonly used distribution in directional statistics. Definition The probability density function of the wrapped normal distribution is : f_(\theta;\mu,\sigma)=\frac \sum^_ \exp \left frac \right where ''μ'' and ''σ'' are the mean and standard deviation of the unwrapped distribution, respectively. Expressing the above density function in terms of the characteristic function of the normal distribution yields: : f_(\theta;\mu,\sigma)=\frac\sum_^\infty e^ =\frac\vartheta\left(\frac,\frac\right) , where \vartheta(\theta,\tau) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirac Comb
In mathematics, a Dirac comb (also known as shah function, impulse train or sampling function) is a periodic function with the formula \operatorname_(t) \ := \sum_^ \delta(t - k T) for some given period T. Here ''t'' is a real variable and the sum extends over all integers ''k.'' The Dirac delta function \delta and the Dirac comb are tempered distributions. The graph of the function resembles a comb (with the \deltas as the comb's ''teeth''), hence its name and the use of the comb-like Cyrillic letter sha (Ш) to denote the function. The symbol \operatorname\,\,(t), where the period is omitted, represents a Dirac comb of unit period. This implies \operatorname_(t) \ = \frac\operatorname\ \!\!\!\left(\frac\right). Because the Dirac comb function is periodic, it can be represented as a Fourier series based on the Dirichlet kernel: \operatorname_(t) = \frac\sum_^ e^. The Dirac comb function allows one to represent both continuous and discrete phenomena, such as sampling and al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Holomorphic Function
In mathematics, a holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighbourhood of each point in a domain in complex coordinate space . The existence of a complex derivative in a neighbourhood is a very strong condition: it implies that a holomorphic function is infinitely differentiable and locally equal to its own Taylor series (''analytic''). Holomorphic functions are the central objects of study in complex analysis. Though the term ''analytic function'' is often used interchangeably with "holomorphic function", the word "analytic" is defined in a broader sense to denote any function (real, complex, or of more general type) that can be written as a convergent power series in a neighbourhood of each point in its domain. That all holomorphic functions are complex analytic functions, and vice versa, is a major theorem in complex analysis. Holomorphic functions are also sometimes referred to as ''regular fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poisson Kernel
In mathematics, and specifically in potential theory, the Poisson kernel is an integral kernel, used for solving the two-dimensional Laplace equation, given Dirichlet boundary conditions on the unit disk. The kernel can be understood as the derivative of the Green's function for the Laplace equation. It is named for Siméon Poisson. Poisson kernels commonly find applications in control theory and two-dimensional problems in electrostatics. In practice, the definition of Poisson kernels are often extended to ''n''-dimensional problems. Two-dimensional Poisson kernels On the unit disc In the complex plane, the Poisson kernel for the unit disc is given by P_r(\theta) = \sum_^\infty r^e^ = \frac = \operatorname\left(\frac\right), \ \ \ 0 \le r < 1. This can be thought of in two ways: either as a function of ''r'' and ''θ'', or as a family of functions of ''θ'' indexed by ''r''. If is the open |
McCullagh's Parametrization Of The Cauchy Distributions
In probability theory, the "standard" Cauchy distribution is the probability distribution whose probability density function (pdf) is :f(x) = for ''x'' real. This has median 0, and first and third quartiles respectively −1 and +1. Generally, a Cauchy distribution is any probability distribution belonging to the same location-scale family as this one. Thus, if ''X'' has a standard Cauchy distribution and ''μ'' is any real number and ''σ'' > 0, then ''Y'' = ''μ'' + ''σX'' has a Cauchy distribution whose median is ''μ'' and whose first and third quartiles are respectively ''μ'' − ''σ'' and ''μ'' + ''σ''. McCullagh's parametrization, introduced by Peter McCullagh, professor of statistics at the University of Chicago, uses the two parameters of the non-standardised distribution to form a single complex-valued parameter, specifically, the complex number ''θ'' = ''μ'' + ''iσ'', where ''i'' is the imag ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Academic Press
Academic Press (AP) is an academic book publisher founded in 1941. It was acquired by Harcourt, Brace & World in 1969. Reed Elsevier bought Harcourt in 2000, and Academic Press is now an imprint of Elsevier. Academic Press publishes reference books, serials and online products in the subject areas of: * Communications engineering * Economics * Environmental science * Finance * Food science and nutrition * Geophysics * Life sciences * Mathematics and statistics * Neuroscience * Physical sciences * Psychology Well-known products include the ''Methods in Enzymology'' series and encyclopedias such as ''The International Encyclopedia of Public Health'' and the ''Encyclopedia of Neuroscience''. See also * Akademische Verlagsgesellschaft (AVG) — the German predecessor, founded in 1906 by Leo Jolowicz (1868–1940), the father of Walter Jolowicz Walter may refer to: People * Walter (name), both a surname and a given name * Little Walter, American blues harmonica player Marion Wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Closed Form Expression
In mathematics, a closed-form expression is a mathematical expression that uses a finite number of standard operations. It may contain constants, variables, certain well-known operations (e.g., + − × ÷), and functions (e.g., ''n''th root, exponent, logarithm, trigonometric functions, and inverse hyperbolic functions), but usually no limit, differentiation, or integration. The set of operations and functions may vary with author and context. Example: roots of polynomials The solutions of any quadratic equation with complex coefficients can be expressed in closed form in terms of addition, subtraction, multiplication, division, and square root extraction, each of which is an elementary function. For example, the quadratic equation :ax^2+bx+c=0, is tractable since its solutions can be expressed as a closed-form expression, i.e. in terms of elementary functions: :x=\frac. Similarly, solutions of cubic and quartic (third and fourth degree) equations can be expressed u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
