|
Variable-range Hopping
Variable-range hopping is a model used to describe carrier transport in a disordered semiconductor or in amorphous solid by hopping in an extended temperature range. It has a characteristic temperature dependence of :\sigma= \sigma_0e^ where \sigma is the conductivity and \beta is a parameter dependent on the model under consideration. Mott variable-range hopping The Nevill Francis Mott, Mott variable-range hopping describes low-temperature Electrical conduction, conduction in strongly disordered systems with Anderson localization, localized charge-carrier states and has a characteristic temperature dependence of :\sigma= \sigma_0e^ for three-dimensional conductance (with \beta = 1/4), and is generalized to ''d''-dimensions :\sigma= \sigma_0e^. Hopping conduction at low temperatures is of great interest because of the savings the semiconductor industry could achieve if they were able to replace single-crystal devices with glass layers. Derivation The original Mott paper intr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Semiconductor
A semiconductor is a material with electrical conductivity between that of a conductor and an insulator. Its conductivity can be modified by adding impurities (" doping") to its crystal structure. When two regions with different doping levels are present in the same crystal, they form a semiconductor junction. The behavior of charge carriers, which include electrons, ions, and electron holes, at these junctions is the basis of diodes, transistors, and most modern electronics. Some examples of semiconductors are silicon, germanium, gallium arsenide, and elements near the so-called " metalloid staircase" on the periodic table. After silicon, gallium arsenide is the second-most common semiconductor and is used in laser diodes, solar cells, microwave-frequency integrated circuits, and others. Silicon is a critical element for fabricating most electronic circuits. Semiconductor devices can display a range of different useful properties, such as passing current more easil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Amorphous Solid
In condensed matter physics and materials science, an amorphous solid (or non-crystalline solid) is a solid that lacks the long-range order that is a characteristic of a crystal. The terms "glass" and "glassy solid" are sometimes used synonymously with amorphous solid; however, these terms refer specifically to amorphous materials that undergo a glass transition. Examples of amorphous solids include glasses, metallic glasses, and certain types of plastics and polymers. Etymology The term "Amorphous" comes from the Greek language, Greek ''a'' ("without"), and ''morphé'' ("shape, form"). Structure Amorphous materials have an internal structure of molecular-scale structural blocks that can be similar to the basic structural units in the crystalline phase of the same compound. Unlike in crystalline materials, however, no long-range regularity exists: amorphous materials cannot be described by the repetition of a finite unit cell. Statistical measures, such as the atomic density ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Nevill Francis Mott
Sir Nevill Francis Mott (30 September 1905 – 8 August 1996) was a British physicist who won the Nobel Prize for Physics in 1977 for his work on the electronic structure of magnetic and disordered systems, especially amorphous semiconductors. The award was shared with Philip W. Anderson and J. H. Van Vleck. The three had conducted loosely related research. Mott and Anderson clarified the reasons why magnetic or amorphous materials can sometimes be metallic and sometimes insulating. Education and early life Mott was born in Leeds to Charles Francis Mott and Lilian Mary Reynolds, a granddaughter of Sir John Richardson, and great granddaughter of Sir John Henry Pelly, 1st Baronet. Miss Reynolds was a Cambridge Mathematics Tripos graduate and at Cambridge was the best woman mathematician of her year. His parents met in the Cavendish Laboratory, when both were engaged in physics research under J.J. Thomson. Nevill grew up first in the village of Giggleswick, in the West ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Electrical Conduction
Electrical resistivity (also called volume resistivity or specific electrical resistance) is a fundamental specific property of a material that measures its electrical resistance or how strongly it resists electric current. A low resistivity indicates a material that readily allows electric current. Resistivity is commonly represented by the Greek letter (rho). The SI unit of electrical resistivity is the ohm-metre (Ω⋅m). For example, if a solid cube of material has sheet contacts on two opposite faces, and the resistance between these contacts is , then the resistivity of the material is . Electrical conductivity (or specific conductance) is the reciprocal of electrical resistivity. It represents a material's ability to conduct electric current. It is commonly signified by the Greek letter (sigma), but ( kappa) (especially in electrical engineering) and (gamma) are sometimes used. The SI unit of electrical conductivity is siemens per metre (S/ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Anderson Localization
In condensed matter physics, Anderson localization (also known as strong localization) is the absence of diffusion of waves in a ''disordered'' medium. This phenomenon is named after the American physicist P. W. Anderson, who was the first to suggest that electron localization is possible in a lattice potential, provided that the degree of randomness (disorder) in the lattice is sufficiently large, as can be realized for example in a semiconductor with impurities or defects. Anderson localization is a general wave phenomenon that applies to the transport of electromagnetic waves, acoustic waves, quantum waves, spin waves, etc. This phenomenon is to be distinguished from weak localization, which is the precursor effect of Anderson localization (see below), and from Mott localization, named after Sir Nevill Mott, where the transition from metallic to insulating behaviour is ''not'' due to disorder, but to a strong mutual Coulomb repulsion of electrons. Introduction In the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Attenuation Length
In physics, the attenuation length or absorption length is the distance into a material when the probability has dropped to that a particle has ''not'' been absorbed. Alternatively, if there is a beam of particles incident on the material, the attenuation length is the distance where the intensity of the beam has dropped to , or about 63% of the particles have been stopped. Mathematically, the probability of finding a particle at depth into the material is calculated by the Beer–Lambert law: :P(x) = e^ \!\,. In general is material- and energy-dependent. See also * Beer's Law * Mean free path * Attenuation coefficient * Attenuation (electromagnetic radiation) * Radiation length In particle physics, the radiation length is a characteristic of a material, related to the energy loss of high energy elementary particle, particles electromagnetically interacting with it. It is defined as the mean length (in cm) into the mate ... References * * https://web.archive.org/ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Gamma Function
In mathematics, the gamma function (represented by Γ, capital Greek alphabet, Greek letter gamma) is the most common extension of the factorial function to complex numbers. Derived by Daniel Bernoulli, the gamma function \Gamma(z) is defined for all complex numbers z except non-positive integers, and for every positive integer z=n, \Gamma(n) = (n-1)!\,.The gamma function can be defined via a convergent improper integral for complex numbers with positive real part: \Gamma(z) = \int_0^\infty t^ e^\textt, \ \qquad \Re(z) > 0\,.The gamma function then is defined in the complex plane as the analytic continuation of this integral function: it is a meromorphic function which is holomorphic function, holomorphic except at zero and the negative integers, where it has simple Zeros and poles, poles. The gamma function has no zeros, so the reciprocal gamma function is an entire function. In fact, the gamma function corresponds to the Mellin transform of the negative exponential functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Density Of States
In condensed matter physics, the density of states (DOS) of a system describes the number of allowed modes or quantum state, states per unit energy range. The density of states is defined as where N(E)\delta E is the number of states in the system of volume V whose energies lie in the range from E to E+\delta E. It is mathematically represented as a distribution by a probability density function, and it is generally an average over the space and time domains of the various states occupied by the system. The density of states is directly related to the dispersion relations of the properties of the system. High DOS at a specific energy level means that many states are available for occupation. Generally, the density of states of matter is continuous. In isolated systems however, such as atoms or molecules in the gas phase, the density distribution is Discrete distribution, discrete, like a spectral density. Local variations, most often due to distortions of the original system, are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Power Law
In statistics, a power law is a Function (mathematics), functional relationship between two quantities, where a Relative change and difference, relative change in one quantity results in a relative change in the other quantity proportional to the change raised to a constant exponent: one quantity varies as a power of another. The change is independent of the initial size of those quantities. For instance, the area of a square has a power law relationship with the length of its side, since if the length is doubled, the area is multiplied by 2, while if the length is tripled, the area is multiplied by 3, and so on. Empirical examples The distributions of a wide variety of physical, biological, and human-made phenomena approximately follow a power law over a wide range of magnitudes: these include the sizes of craters on the moon and of solar flares, cloud sizes, the foraging pattern of various species, the sizes of activity patterns of neuronal populations, the frequencies of words ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
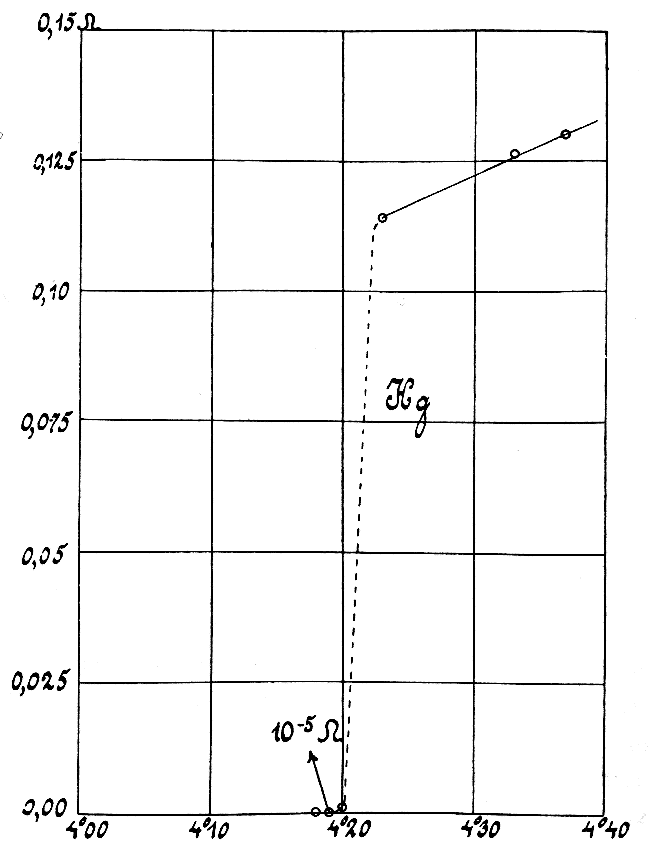
Coulomb Gap
First introduced by M. Pollak, the Coulomb gap is a soft gap in the single-particle density of states (DOS) of a system of interacting localized electrons. Due to the long-range Coulomb interactions, the single-particle DOS vanishes at the chemical potential, at low enough temperatures, such that thermal excitations do not wash out the gap. Theory At zero temperature, a classical treatment of a system gives an upper bound for the DOS near the Fermi energy, first suggested by Efros and Shklovskii. The argument is as follows: Let us look at the ground state configuration of the system. Defining E_i as the energy of an electron at site i , due to the disorder and the Coulomb interaction with all other electrons (we define this both for occupied and unoccupied sites), it is easy to see that the energy needed to move an electron from an occupied site i to an unoccupied site j is given by the expression: :\Delta E=E_j-E_i-e^2/r_ . The subtraction of the last term accounts ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Fermi Level
The Fermi level of a solid-state body is the thermodynamic work required to add one electron to the body. It is a thermodynamic quantity usually denoted by ''μ'' or ''E''F for brevity. The Fermi level does not include the work required to remove the electron from wherever it came from. A precise understanding of the Fermi level—how it relates to electronic band structure in determining electronic properties; how it relates to the voltage and flow of charge in an electronic circuit—is essential to an understanding of solid-state physics. In band structure theory, used in solid state physics to analyze the energy levels in a solid, the Fermi level can be considered to be a hypothetical energy level of an electron, such that at thermodynamic equilibrium this energy level would have a ''50% probability of being occupied at any given time''. The position of the Fermi level in relation to the band energy levels is a crucial factor in determining electrical properties. The Fer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Alexei L
Alexey ( ; ), is a Russian and Bulgarian male given name derived from the Greek ''Aléxios'' (), meaning "Defender", and thus of the same origin as the Latin Alexius. Similar Ukrainian and Belarusian names are romanized as Oleksii (Олексій) and Aliaksiej (Аляксей), respectively. The Russian Orthodox Church uses the Old Church Slavonic version, Alexiy or Aleksiy (Алексiй, or Алексий in modern spelling), for its Saints and hierarchs (most notably, this is the form used for Patriarchs Alexius I and Alexius II). The name became fairly popular in Russia after the baptism of Michael of Russia's son, Alexis of Russia. The common hypocoristic is Alyosha () or simply Lyosha (). These may be further transformed into Alyoshka, Alyoshenka, Lyoshka, Lyoha, Lyoshenka (, respectively), sometimes rendered as Alesha/Aleshenka in English. The form Alyosha may be used as a full first name in Bulgaria (Альоша) and Armenia. In theory, Alexia is the femal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |