|
Vanna–Volga Pricing
The Vanna–Volga method is a mathematical tool used in finance. It is a technique for pricing first-generation exotic options in foreign exchange market Foreign exchange derivative, (FX) derivatives. Description It consists of adjusting the Black–Scholes theoretical value (BSTV) by the cost of a portfolio which hedges three main risks associated to the volatility of the option: the Greeks (finance), Vega \mathcal, the Vanna and the Volga. The Vanna is the sensitivity of the Vega with respect to a change in the spot FX rate: \textrm = \frac. Similarly, the Volga is the sensitivity of the Vega with respect to a change of the implied volatility \sigma: \textrm= \frac. If we consider a Volatility smile, smile volatility term structure \sigma(K) with ATM strike K_0, ATM volatility \sigma_0, 25-Delta call/put volatilities \sigma(K_), and where K_ are the 25-Delta call/put strikes (obtained by solving the equations \Delta_(K_c,\sigma(K_c))=1/4 and \Delta_(K_p,\sigma(K_p))=-1/4 wher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finance
Finance is the study and discipline of money, currency and capital assets. It is related to, but not synonymous with economics, the study of production, distribution, and consumption of money, assets, goods and services (the discipline of financial economics bridges the two). Finance activities take place in financial systems at various scopes, thus the field can be roughly divided into personal, corporate, and public finance. In a financial system, assets are bought, sold, or traded as financial instruments, such as currencies, loans, bonds, shares, stocks, options, futures, etc. Assets can also be banked, invested, and insured to maximize value and minimize loss. In practice, risks are always present in any financial action and entities. A broad range of subfields within finance exist due to its wide scope. Asset, money, risk and investment management aim to maximize value and minimize volatility. Financial analysis is viability, stability, and profitability asse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exotic Option
In finance, an exotic option is an option which has features making it more complex than commonly traded vanilla options. Like the more general exotic derivatives they may have several triggers relating to determination of payoff. An exotic option may also include a non-standard underlying instrument, developed for a particular client or for a particular market. Exotic options are more complex than options that trade on an exchange, and are generally traded over-the-counter. Etymology The term "exotic option" was popularized by Mark Rubinstein's 1990 working paper (published 1992, with Eric Reiner) "Exotic Options", with the term based either on exotic wagers in horse racing, or due to the use of international terms such as "Asian option", suggesting the "exotic Orient". Journalist Brian Palmer used the "successful $1 bet on the superfecta" in the 2010 Kentucky Derby that "paid a whopping $101,284.60" as an example of the controversial high-risk, high-payout exotic bets that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Foreign Exchange Market
The foreign exchange market (Forex, FX, or currency market) is a global decentralized or over-the-counter (OTC) market for the trading of currencies. This market determines foreign exchange rates for every currency. It includes all aspects of buying, selling and exchanging currencies at current or determined prices. In terms of trading volume, it is by far the largest market in the world, followed by the credit market. The main participants in this market are the larger international banks. Financial centers around the world function as anchors of trading between a wide range of multiple types of buyers and sellers around the clock, with the exception of weekends. Since currencies are always traded in pairs, the foreign exchange market does not set a currency's absolute value but rather determines its relative value by setting the market price of one currency if paid for with another. Ex: USD 1 is worth X CAD, or CHF, or JPY, etc. The foreign exchange market works thro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Foreign Exchange Derivative
A foreign exchange derivative is a financial derivative whose payoff depends on the foreign exchange rates of two (or more) currencies. These instruments are commonly used for currency speculation and arbitrage or for hedging foreign exchange risk. History Foreign exchange transactions can be traced back to the fourteenth Century in the UK, but the coming into being and development of foreign exchange derivatives market was in the 1970s with the historical background and economic environment. Firstly, after the collapse of the Bretton Woods system, in 1976, IMF held a meeting in Jamaica and reached the Jamaica agreement. When the floating exchange-rate system replaced a fixed exchange-rate system, many countries relaxed control of interest rates and the risk of financial market increased. In order to reduce and avoid risks and achieve the purpose of hedging, modern financial derivatives came into being. Secondly, economic globalization promoted the globalization of f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
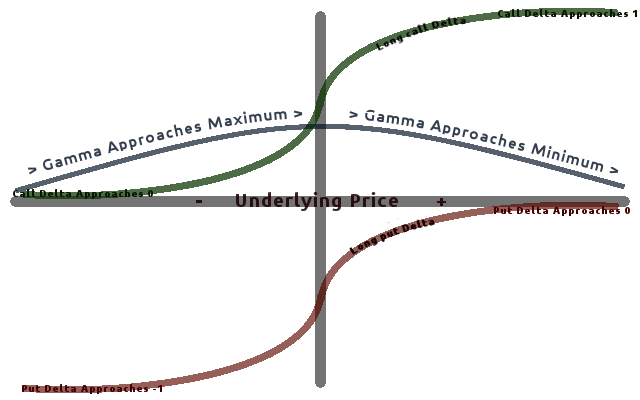
Greeks (finance)
In mathematical finance, the Greeks are the quantities representing the sensitivity of the price of derivatives such as options to a change in underlying parameters on which the value of an instrument or portfolio of financial instruments is dependent. The name is used because the most common of these sensitivities are denoted by Greek letters (as are some other finance measures). Collectively these have also been called the risk sensitivities, risk measures or hedge parameters. Use of the Greeks The Greeks are vital tools in risk management. Each Greek measures the sensitivity of the value of a portfolio to a small change in a given underlying parameter, so that component risks may be treated in isolation, and the portfolio rebalanced accordingly to achieve a desired exposure; see for example delta hedging. The Greeks in the Black–Scholes model are relatively easy to calculate, a desirable property of financial models, and are very useful for derivatives traders, especi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Implied Volatility
In financial mathematics, the implied volatility (IV) of an option contract is that value of the volatility of the underlying instrument which, when input in an option pricing model (such as Black–Scholes), will return a theoretical value equal to the current market price of said option. A non-option financial instrument that has embedded optionality, such as an interest rate cap, can also have an implied volatility. Implied volatility, a forward-looking and subjective measure, differs from historical volatility because the latter is calculated from known past returns of a security. To understand where implied volatility stands in terms of the underlying, implied volatility rank is used to understand its implied volatility from a one-year high and low IV. Motivation An option pricing model, such as Black–Scholes, uses a variety of inputs to derive a theoretical value for an option. Inputs to pricing models vary depending on the type of option being priced and the pricing m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volatility Smile
Volatility smiles are implied volatility patterns that arise in pricing financial options. It is a parameter (implied volatility) that is needed to be modified for the Black–Scholes formula to fit market prices. In particular for a given expiration, options whose strike price differs substantially from the underlying asset's price command higher prices (and thus implied volatilities) than what is suggested by standard option pricing models. These options are said to be either deep in-the-money or out-of-the-money. Graphing implied volatilities against strike prices for a given expiry produces a skewed "smile" instead of the expected flat surface. The pattern differs across various markets. Equity options traded in American markets did not show a volatility smile before the Crash of 1987 but began showing one afterwards. It is believed that investor reassessments of the probabilities of fat-tail have led to higher prices for out-of-the-money options. This anomaly implies de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Finance
Mathematical finance, also known as quantitative finance and financial mathematics, is a field of applied mathematics, concerned with mathematical modeling of financial markets. In general, there exist two separate branches of finance that require advanced quantitative techniques: derivatives pricing on the one hand, and risk and portfolio management on the other. Mathematical finance overlaps heavily with the fields of computational finance and financial engineering. The latter focuses on applications and modeling, often by help of stochastic asset models, while the former focuses, in addition to analysis, on building tools of implementation for the models. Also related is quantitative investing, which relies on statistical and numerical models (and lately machine learning) as opposed to traditional fundamental analysis when managing portfolios. French mathematician Louis Bachelier's doctoral thesis, defended in 1900, is considered the first scholarly work on mathematical fina ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivatives (finance)
The derivative of a function is the rate of change of the function's output relative to its input value. Derivative may also refer to: In mathematics and economics *Brzozowski derivative in the theory of formal languages *Formal derivative, an operation on elements of a polynomial ring which mimics the form of the derivative from calculus * Radon–Nikodym derivative in measure theory *Derivative (set theory), a concept applicable to normal functions *Derivative (graph theory), an alternative term for a line graph deva *Derivative (finance), a contract whose value is derived from that of other quantities *Derivative suit or derivative action, a type of lawsuit filed by shareholders of a corporation In science and engineering *Derivative (chemistry), a type of compound which is a product of the process of derivatization *Derivative (linguistics), the process of forming a new word on the basis of an existing word, e.g. happiness and unhappy from happy * Aeroderivative gas turbine, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Portfolio Theories
Portfolio may refer to: Objects * Portfolio (briefcase), a type of briefcase Collections * Portfolio (finance), a collection of assets held by an institution or a private individual * Artist's portfolio, a sample of an artist's work or a case used to display artwork, photographs etc. * Career portfolio, an organized presentation of an individual's education, work samples, and skills * Electronic portfolio, a collection of electronic documents * IT portfolio, in IT portfolio management, the portfolio of large classes of items of enterprise Information Technology * Patent portfolio, a collection of patents owned by a single entity * Project portfolio, in project portfolio management, the portfolio of projects in an organization * Ministry (government department), the post and responsibilities of a head of a government department Computing * Atari Portfolio, a palmtop computer * Extensis Portfolio, a digital asset manager Media * ''The Portfolio'', a British fine arts ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
