|
Van Der Waerden Notation
In theoretical physics, Van der Waerden notation refers to the usage of two-component spinors (Weyl spinors) in four spacetime dimensions. This is standard in twistor theory and supersymmetry. It is named after Bartel Leendert van der Waerden. Dotted indices ;Undotted indices (chiral indices) Spinors with lower undotted indices have a left-handed chirality, and are called chiral indices. :\Sigma_\mathrm = \begin \psi_\\ 0 \end ;Dotted indices (anti-chiral indices) Spinors with raised dotted indices, plus an overbar on the symbol (not index), are right-handed, and called anti-chiral indices. :\Sigma_\mathrm = \begin 0 \\ \bar^\\ \end Without the indices, i.e. "index free notation", an overbar is retained on right-handed spinor, since ambiguity arises between chirality when no index is indicated. Hatted indices Indices which have hats are called Dirac indices, and are the set of dotted and undotted, or chiral and anti-chiral, indices. For example, if : \alpha = 1,2\,,\d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theoretical Physics
Theoretical physics is a branch of physics that employs mathematical models and abstractions of physical objects and systems to rationalize, explain and predict natural phenomena. This is in contrast to experimental physics, which uses experimental tools to probe these phenomena. The advancement of science generally depends on the interplay between experimental studies and theory. In some cases, theoretical physics adheres to standards of mathematical rigour while giving little weight to experiments and observations.There is some debate as to whether or not theoretical physics uses mathematics to build intuition and illustrativeness to extract physical insight (especially when normal experience fails), rather than as a tool in formalizing theories. This links to the question of it using mathematics in a less formally rigorous, and more intuitive or heuristic way than, say, mathematical physics. For example, while developing special relativity, Albert Einstein was concerned wit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
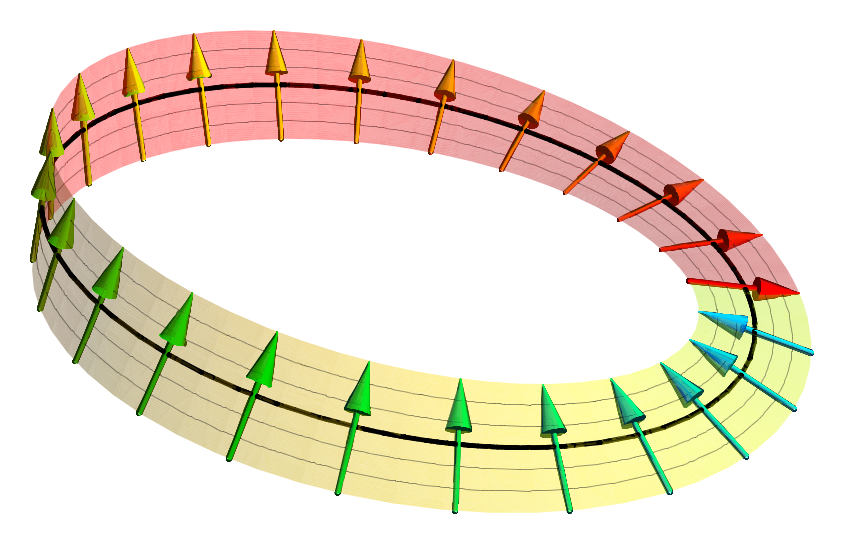
Spinor
In geometry and physics, spinors are elements of a complex vector space that can be associated with Euclidean space. Like geometric vectors and more general tensors, spinors transform linearly when the Euclidean space is subjected to a slight (infinitesimal) rotation. Unlike vectors and tensors, a spinor transforms to its negative when the space is continuously rotated through a complete turn from 0° to 360° (see picture). This property characterizes spinors: spinors can be viewed as the "square roots" of vectors (although this is inaccurate and may be misleading; they are better viewed as "square roots" of sections of vector bundles – in the case of the exterior algebra bundle of the cotangent bundle, they thus become "square roots" of differential forms). It is also possible to associate a substantially similar notion of spinor to Minkowski space, in which case the Lorentz transformations of special relativity play the role of rotations. Spinors were introduced in geome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weyl Spinor
In physics, particularly in quantum field theory, the Weyl equation is a relativistic wave equation for describing massless spin-1/2 particles called Weyl fermions. The equation is named after Hermann Weyl. The Weyl fermions are one of the three possible types of elementary fermions, the other two being the Dirac and the Majorana fermions. None of the elementary particles in the Standard Model are Weyl fermions. Previous to the confirmation of the neutrino oscillations, it was considered possible that the neutrino might be a Weyl fermion (it is now expected to be either a Dirac or a Majorana fermion). In condensed matter physics, some materials can display quasiparticles that behave as Weyl fermions, leading to the notion of Weyl semimetals. Mathematically, any Dirac fermion can be decomposed as two Weyl fermions of opposite chirality coupled by the mass term. History The Dirac equation, was published in 1928 by Paul Dirac, first describing spin-½ particles in the framework ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Twistor Theory
In theoretical physics, twistor theory was proposed by Roger Penrose in 1967 as a possible path to quantum gravity and has evolved into a branch of theoretical and mathematical physics. Penrose proposed that twistor space should be the basic arena for physics from which space-time itself should emerge. It leads to a powerful set of mathematical tools that have applications to differential and integral geometry, nonlinear differential equations and representation theory and in physics to general relativity and quantum field theory, in particular to scattering amplitudes. Development seems to be indirectly influenced by Einstein–Cartan–Sciama–Kibble theory. Overview Mathematically, projective twistor space \mathbb is a 3-dimensional complex manifold, complex projective 3-space \mathbb^3. It has the physical interpretation of the space of massless particles with spin. It is the projectivisation of a 4-dimensional complex vector space, non-projective twistor space \mathbb w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Supersymmetry
In a supersymmetric theory the equations for force and the equations for matter are identical. In theoretical and mathematical physics, any theory with this property has the principle of supersymmetry (SUSY). Dozens of supersymmetric theories exist. Supersymmetry is a spacetime symmetry between two basic classes of particles: bosons, which have an integer-valued spin and follow Bose–Einstein statistics, and fermions, which have a half-integer-valued spin and follow Fermi–Dirac statistics. In supersymmetry, each particle from one class would have an associated particle in the other, known as its superpartner, the spin of which differs by a half-integer. For example, if the electron exists in a supersymmetric theory, then there would be a particle called a ''"selectron"'' (superpartner electron), a bosonic partner of the electron. In the simplest supersymmetry theories, with perfectly " unbroken" supersymmetry, each pair of superpartners would share the same mass and intern ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bartel Leendert Van Der Waerden
Bartel Leendert van der Waerden (; 2 February 1903 – 12 January 1996) was a Dutch mathematician and historian of mathematics. Biography Education and early career Van der Waerden learned advanced mathematics at the University of Amsterdam and the University of Göttingen, from 1919 until 1926. He was much influenced by Emmy Noether at Göttingen, Germany. Amsterdam awarded him a Ph.D. for a thesis on algebraic geometry, supervised by Hendrick de Vries. Göttingen awarded him the habilitation in 1928. In that year, at the age of 25, he accepted a professorship at the University of Groningen. In his 27th year, Van der Waerden published his ''Moderne Algebra'', an influential two-volume treatise on abstract algebra, still cited, and perhaps the first treatise to treat the subject as a comprehensive whole. This work systematized an ample body of research by Emmy Noether, David Hilbert, Richard Dedekind, and Emil Artin. In the following year, 1931, he was appointed professor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirac Adjoint
In quantum field theory, the Dirac adjoint defines the dual operation of a Dirac spinor. The Dirac adjoint is motivated by the need to form well-behaved, measurable quantities out of Dirac spinors, replacing the usual role of the Hermitian adjoint. Possibly to avoid confusion with the usual Hermitian adjoint, some textbooks do not provide a name for the Dirac adjoint but simply call it "ψ-bar". Definition Let \psi be a Dirac spinor. Then its Dirac adjoint is defined as :\bar\psi \equiv \psi^\dagger \gamma^0 where \psi^\dagger denotes the Hermitian adjoint of the spinor \psi, and \gamma^0 is the time-like gamma matrix. Spinors under Lorentz transformations The Lorentz group of special relativity is not compact, therefore spinor representations of Lorentz transformations are generally not unitary. That is, if \lambda is a projective representation of some Lorentz transformation, :\psi \mapsto \lambda \psi, then, in general, :\lambda^\dagger \ne \lambda^. The Hermit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirac Equation
In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin- massive particles, called "Dirac particles", such as electrons and quarks for which parity is a symmetry. It is consistent with both the principles of quantum mechanics and the theory of special relativity, and was the first theory to account fully for special relativity in the context of quantum mechanics. It was validated by accounting for the fine structure of the hydrogen spectrum in a completely rigorous way. The equation also implied the existence of a new form of matter, ''antimatter'', previously unsuspected and unobserved and which was experimentally confirmed several years later. It also provided a ''theoretical'' justification for the introduction of several component wave functions in Pauli's phenomenological theory of spin. The wave functions in the Dirac theo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infeld–Van Der Waerden Symbols
The Infeld–Van der Waerden symbols, sometimes called simply Van der Waerden symbols, are an invariant symbol associated to the Lorentz group used in quantum field theory. They are named after Leopold Infeld and Bartel Leendert van der Waerden. The Infeld–Van der Waerden symbols are index notation for Clifford multiplication of covectors on left handed spinors giving a right-handed spinors or vice versa, i.e. they are off diagonal blocks of gamma matrices. The symbols are typically denoted in Van der Waerden notation as \sigma^m_\quad\text\quad\bar^. and so have one Lorentz index (m), one left-handed (undotted Greek), and one right-handed (dotted Greek) Weyl spinor index. They satisfy \begin \sigma^m_\bar^ + \sigma^n_\bar^ &= 2\delta_\alpha^\gamma g^, \quad \\ \sigma^m_\bar^ + \sigma^n_\bar^ &= 2 \delta_^ g^. \end They need not be constant, however, and can therefore be formulated on curved space time. Background The existence of thi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lorentz Transformation
In physics, the Lorentz transformations are a six-parameter family of linear transformations from a coordinate frame in spacetime to another frame that moves at a constant velocity relative to the former. The respective inverse transformation is then parameterized by the negative of this velocity. The transformations are named after the Dutch physicist Hendrik Lorentz. The most common form of the transformation, parametrized by the real constant v, representing a velocity confined to the -direction, is expressed as \begin t' &= \gamma \left( t - \frac \right) \\ x' &= \gamma \left( x - v t \right)\\ y' &= y \\ z' &= z \end where and are the coordinates of an event in two frames with the origins coinciding at 0, where the primed frame is seen from the unprimed frame as moving with speed along the -axis, where is the speed of light, and \gamma = \left ( \sqrt\right )^ is the Lorentz factor. When speed is much smaller than , the Lorentz factor is negligibly different from 1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pauli Equation
In quantum mechanics, the Pauli equation or Schrödinger–Pauli equation is the formulation of the Schrödinger equation for spin-½ particles, which takes into account the interaction of the particle's spin with an external electromagnetic field. It is the non- relativistic limit of the Dirac equation and can be used where particles are moving at speeds much less than the speed of light, so that relativistic effects can be neglected. It was formulated by Wolfgang Pauli in 1927. Equation For a particle of mass m and electric charge q, in an electromagnetic field described by the magnetic vector potential \mathbf and the electric scalar potential \phi, the Pauli equation reads: Here \boldsymbol = (\sigma_x, \sigma_y, \sigma_z) are the Pauli operators collected into a vector for convenience, and \mathbf = -i\hbar \nabla is the momentum operator in position representation. The state of the system, , \psi\rangle (written in Dirac notation), can be considered as a two-componen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ricci Calculus
In mathematics, Ricci calculus constitutes the rules of index notation and manipulation for tensors and tensor fields on a differentiable manifold, with or without a metric tensor or connection. It is also the modern name for what used to be called the absolute differential calculus (the foundation of tensor calculus), developed by Gregorio Ricci-Curbastro in 1887–1896, and subsequently popularized in a paper written with his pupil Tullio Levi-Civita in 1900. Jan Arnoldus Schouten developed the modern notation and formalism for this mathematical framework, and made contributions to the theory, during its applications to general relativity and differential geometry in the early twentieth century. A component of a tensor is a real number that is used as a coefficient of a basis element for the tensor space. The tensor is the sum of its components multiplied by their corresponding basis elements. Tensors and tensor fields can be expressed in terms of their components, and operatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |