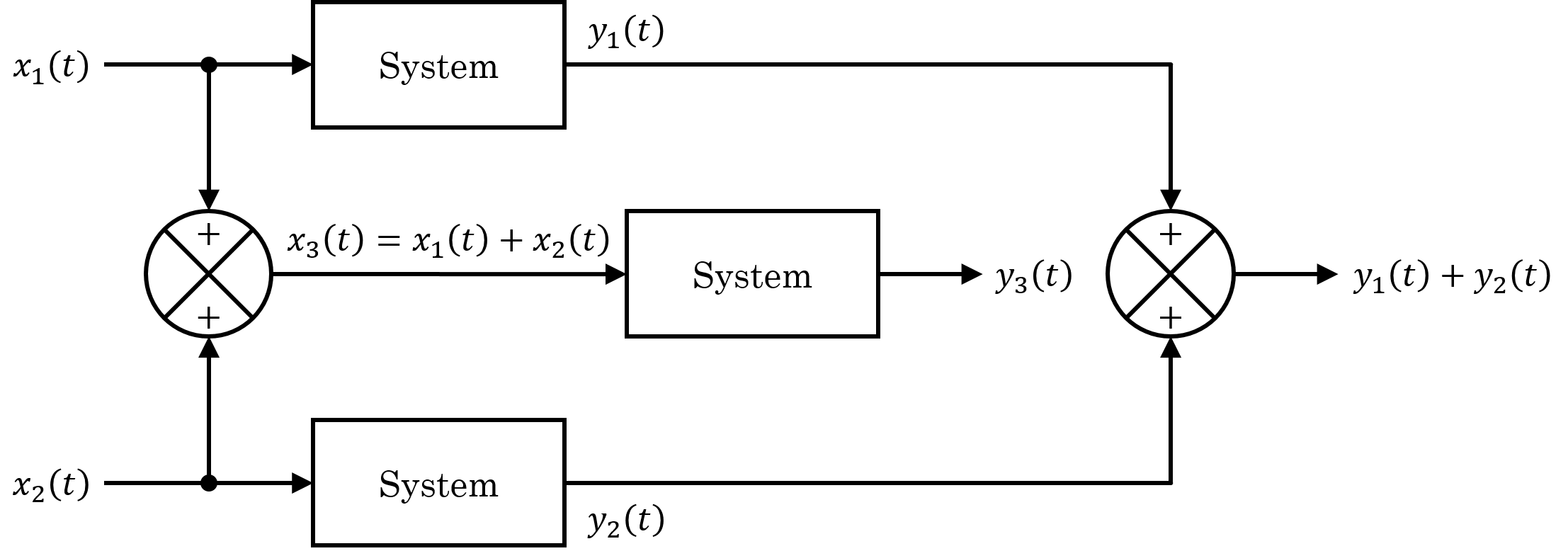
|
Valuation Algebra
The term "information algebra" refers to mathematical techniques of information processing. Classical information theory goes back to Claude Shannon. It is a theory of information transmission, looking at communication and storage. However, it has not been considered so far that information comes from different sources and that it is therefore usually combined. It has furthermore been neglected in classical information theory that one wants to extract those parts out of a piece of information that are relevant to specific questions. A mathematical phrasing of these operations leads to an algebra of information, describing basic modes of information processing. Such an algebra involves several formalisms of computer science, which seem to be different on the surface: relational databases, multiple systems of formal logic or numerical problems of linear algebra. It allows the development of generic procedures of information processing and thus a unification of basic methods of compute ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Processing
Information processing is the change (processing) of information in any manner detectable by an observer. As such, it is a process that ''describes'' everything that happens (changes) in the universe, from the falling of a rock (a change in position) to the printing of a text file from a digital computer system. In the latter case, an information processor (the printer) is changing the form of presentation of that text file (from bytes to glyphs). The computers up to this period function on the basis of programs saved in the memory, having no intelligence of their own. In cognitive psychology Within the field of cognitive psychology, information processing is an approach to the goal of understanding human thinking in relation to how they process the same kind of information as computers (Shannon & Weaver, 1963). It arose in the 1940s and 1950s, after World War II (Sternberg & Sternberg, 2012). The approach treats cognition as essentially computational in nature, with ''mind'' b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semiring Valued Algebra
In abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse. The term rig is also used occasionally—this originated as a joke, suggesting that rigs are ri''n''gs without ''n''egative elements, similar to using '' rng'' to mean a r''i''ng without a multiplicative ''i''dentity. Tropical semirings are an active area of research, linking algebraic varieties with piecewise linear structures. Definition A semiring is a set R equipped with two binary operations \,+\, and \,\cdot,\, called addition and multiplication, such that:Lothaire (2005) p.211Sakarovitch (2009) pp.27–28 * (R, +) is a commutative monoid with identity element 0: ** (a + b) + c = a + (b + c) ** 0 + a = a = a + 0 ** a + b = b + a * (R, \,\cdot\,) is a monoid with identity element 1: ** (a \cdot b) \cdot c = a \cdot (b \cdot c) ** 1 \cdot a = a = a \cdot 1 * Multiplication left and right distributes over addition: ** ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probabilistic Argumentation
Probabilistic argumentation refers to different formal frameworks pertaining to probabilistic logic. All share the idea that qualitative aspects can be captured by an underlying logic, while quantitative aspects of uncertainty can be accounted for by probabilistic measures. Probabilistic argumentation labellings The framework of "probabilistic labellings" refers to probability spaces where the sample space is a set of labellings of argumentation graphs . A labelling of an argumentation graph associates any argument of the graph with a label to reflect the acceptability of the argument within the graph. For example, an argument can be associated with a label "in" (the argument is accepted), "out" (the argument is rejected), or "und" (the status of the argument is undecided — neither accepted nor rejected). Consequently, the approach of probabilistic labellings associates any argument with the probability of a label to reflect the probability of the argument to be labelled as suc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scott Information System
In domain theory, a branch of mathematics and computer science, a Scott information system is a primitive kind of logical deductive system often used as an alternative way of presenting Scott domains. Definition A Scott information system, ''A'', is an ordered triple (T, Con, \vdash) * T \mbox * Con \subseteq \mathcal_f(T) \mbox T * \subseteq (Con \setminus \lbrace \emptyset \rbrace)\times T satisfying # \mbox a \in X \in Con\mboxX \vdash a # \mbox X \vdash Y \mboxY \vdash a \mboxX \vdash a # \mboxX \vdash a \mbox X \cup \ \in Con # \forall a \in T : \ \in Con # \mboxX \in Con \mbox X^\prime\, \subseteq X \mboxX^\prime \in Con. Here X \vdash Y means \forall a \in Y, X \vdash a. Examples Natural numbers The return value of a partial recursive function, which either returns a natural number or goes into an infinite recursion, can be expressed as a simple Scott information system as follows: * T := \mathbb * Con := \ \cup \ * X \vdash a\iff a \in X. That is, the result can either ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scott Domain
In the mathematical fields of order and domain theory, a Scott domain is an algebraic, bounded-complete cpo. They are named in honour of Dana S. Scott, who was the first to study these structures at the advent of domain theory. Scott domains are very closely related to algebraic lattices, being different only in possibly lacking a greatest element. They are also closely related to Scott information systems, which constitute a "syntactic" representation of Scott domains. While the term "Scott domain" is widely used with the above definition, the term "domain" does not have such a generally accepted meaning and different authors will use different definitions; Scott himself used "domain" for the structures now called "Scott domains". Additionally, Scott domains appear with other names like "algebraic semilattice" in some publications. Originally, Dana Scott demanded a complete lattice, and the Russian mathematician Yuri Yershov constructed the isomorphic structure of cpo. But ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Valuation Algebra
The term "information algebra" refers to mathematical techniques of information processing. Classical information theory goes back to Claude Shannon. It is a theory of information transmission, looking at communication and storage. However, it has not been considered so far that information comes from different sources and that it is therefore usually combined. It has furthermore been neglected in classical information theory that one wants to extract those parts out of a piece of information that are relevant to specific questions. A mathematical phrasing of these operations leads to an algebra of information, describing basic modes of information processing. Such an algebra involves several formalisms of computer science, which seem to be different on the surface: relational databases, multiple systems of formal logic or numerical problems of linear algebra. It allows the development of generic procedures of information processing and thus a unification of basic methods of compute ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear System
In systems theory, a linear system is a mathematical model of a system based on the use of a linear operator. Linear systems typically exhibit features and properties that are much simpler than the nonlinear case. As a mathematical abstraction or idealization, linear systems find important applications in automatic control theory, signal processing, and telecommunications. For example, the propagation medium for wireless communication systems can often be modeled by linear systems. Definition A general deterministic system can be described by an operator, that maps an input, as a function of to an output, a type of black box description. A system is linear if and only if it satisfies the superposition principle, or equivalently both the additivity and homogeneity properties, without restrictions (that is, for all inputs, all scaling constants and all time.) The superposition principle means that a linear combination of inputs to the system produces a linear combination ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Module (mathematics)
In mathematics, a module is a generalization of the notion of vector space in which the field of scalars is replaced by a ring. The concept of ''module'' generalizes also the notion of abelian group, since the abelian groups are exactly the modules over the ring of integers. Like a vector space, a module is an additive abelian group, and scalar multiplication is distributive over the operation of addition between elements of the ring or module and is compatible with the ring multiplication. Modules are very closely related to the representation theory of groups. They are also one of the central notions of commutative algebra and homological algebra, and are used widely in algebraic geometry and algebraic topology. Introduction and definition Motivation In a vector space, the set of scalars is a field and acts on the vectors by scalar multiplication, subject to certain axioms such as the distributive law. In a module, the scalars need only be a ring, so the module conc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Predicate Logic
First-order logic—also known as predicate logic, quantificational logic, and first-order predicate calculus—is a collection of formal systems used in mathematics, philosophy, linguistics, and computer science. First-order logic uses quantified variables over non-logical objects, and allows the use of sentences that contain variables, so that rather than propositions such as "Socrates is a man", one can have expressions in the form "there exists x such that x is Socrates and x is a man", where "there exists''"'' is a quantifier, while ''x'' is a variable. This distinguishes it from propositional logic, which does not use quantifiers or relations; in this sense, propositional logic is the foundation of first-order logic. A theory about a topic is usually a first-order logic together with a specified domain of discourse (over which the quantified variables range), finitely many functions from that domain to itself, finitely many predicates defined on that domain, and a set of ax ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyadic Algebra
Polyadic algebras (more recently called Halmos algebras) are algebraic structures introduced by Paul Halmos. They are related to first-order logic analogous to the relationship between Boolean algebras and propositional logic (see Lindenbaum–Tarski algebra). There are other ways to relate first-order logic to algebra, including Tarski's cylindric algebras (when equality is part of the logic) and Lawvere's functorial semantics (a categorical approach). References Further reading *Paul Halmos, ''Algebraic Logic'', Chelsea Publishing The American Mathematical Society (AMS) is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, and serves the national and international community through its publications, meetings ..., New York (1962) Algebraic logic {{mathlogic-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cylindric Algebra
In mathematics, the notion of cylindric algebra, invented by Alfred Tarski, arises naturally in the algebraization of first-order logic with equality. This is comparable to the role Boolean algebras play for propositional logic. Cylindric algebras are Boolean algebras equipped with additional cylindrification operations that model quantification and equality. They differ from polyadic algebras in that the latter do not model equality. Definition of a cylindric algebra A cylindric algebra of dimension \alpha (where \alpha is any ordinal number) is an algebraic structure (A,+,\cdot,-,0,1,c_\kappa,d_)_ such that (A,+,\cdot,-,0,1) is a Boolean algebra, c_\kappa a unary operator on A for every \kappa (called a ''cylindrification''), and d_ a distinguished element of A for every \kappa and \lambda (called a ''diagonal''), such that the following hold: : (C1) c_\kappa 0=0 : (C2) x\leq c_\kappa x : (C3) c_\kappa(x\cdot c_\kappa y)=c_\kappa x\cdot c_\kappa y : (C4) c_\kappa c_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logic
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the science of deductively valid inferences or of logical truths. It is a formal science investigating how conclusions follow from premises in a topic-neutral way. When used as a countable noun, the term "a logic" refers to a logical formal system that articulates a proof system. Formal logic contrasts with informal logic, which is associated with informal fallacies, critical thinking, and argumentation theory. While there is no general agreement on how formal and informal logic are to be distinguished, one prominent approach associates their difference with whether the studied arguments are expressed in formal or informal languages. Logic plays a central role in multiple fields, such as philosophy, mathematics, computer science, and linguistics. Logic studies arguments, which consist of a set of premises together with a conclusion. Premises and conclusions are usually un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
