|
Validated Numerics
Validated numerics, or rigorous computation, verified computation, reliable computation, numerical verification () is numerics including mathematically strict error (rounding error, truncation error, discretization error) evaluation, and it is one field of numerical analysis. For computation, interval arithmetic is most often used, where all results are represented by intervals. Validated numerics were used by Warwick Tucker in order to solve the 14th of Smale's problems, and today it is recognized as a powerful tool for the study of dynamical systems. Importance Computation without verification may cause unfortunate results. Below are some examples. Rump's example In the 1980s, Rump made an example. He made a complicated function and tried to obtain its value. Single precision, double precision, extended precision results seemed to be correct, but its plus-minus sign was different from the true value. Phantom solution Breuer–Plum–McKenna used the spectrum method to solve the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic computation, symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods that attempt to find approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences like economics, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics (predicting the motions of planets, stars and galaxies), numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Quadrature
In analysis, numerical integration comprises a broad family of algorithms for calculating the numerical value of a definite integral. The term numerical quadrature (often abbreviated to quadrature) is more or less a synonym for "numerical integration", especially as applied to one-dimensional integrals. Some authors refer to numerical integration over more than one dimension as cubature; others take "quadrature" to include higher-dimensional integration. The basic problem in numerical integration is to compute an approximate solution to a definite integral :\int_a^b f(x) \, dx to a given degree of accuracy. If is a smooth function integrated over a small number of dimensions, and the domain of integration is bounded, there are many methods for approximating the integral to the desired precision. Numerical integration has roots in the geometrical problem of finding a square with the same area as a given plane figure ('' quadrature'' or ''squaring''), as in the quadrature of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
INTLAB
INTLAB (INTerval LABoratory) is an interval arithmetic libraryS.M. Rump: INTLAB – INTerval LABoratory. In Tibor Csendes, editor, Developments in Reliable Computing, pages 77–104. Kluwer Academic Publishers, Dordrecht, 1999.Moore, R. E., Kearfott, R. B., & Cloud, M. J. (2009). Introduction to Interval Analysis. Society for Industrial and Applied Mathematics.Rump, S. M. (2010). Verification methods: Rigorous results using floating-point arithmetic. Acta Numerica, 19, 287–449.Hargreaves, G. I. (2002). Interval analysis in MATLAB. Numerical Algorithms, (2009.1). using MATLAB and GNU Octave, available in Windows and Linux, macOS. It was developed by S.M. Rump from Hamburg University of Technology The Hamburg University of Technology (in German language, German ''Technische Universität Hamburg'', abbreviated TUHH (HH as acronym of Hamburg state) or TU Hamburg) is a research university in Germany. The university was founded in 1978 and in .... INTLAB was used to develop other MA ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Affine Arithmetic
Affine arithmetic (AA) is a model for self-validated numerical analysis. In AA, the quantities of interest are represented as affine combinations (affine forms) of certain primitive variables, which stand for sources of uncertainty in the data or approximations made during the computation. Affine arithmetic is meant to be an improvement on interval arithmetic (IA), and is similar to generalized interval arithmetic, first-order Taylor arithmetic, the center-slope model, and ellipsoid calculus — in the sense that it is an automatic method to derive first-order guaranteed approximations to general formulas. Affine arithmetic is potentially useful in every numeric problem where one needs guaranteed enclosures to smooth functions, such as solving systems of non-linear equations, analyzing dynamical systems, integrating functions, differential equations, etc. Applications include ray tracing, plotting curves, intersecting implicit and parametric surfaces, error analysis ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interval Arithmetic
Interval arithmetic (also known as interval mathematics; interval analysis or interval computation) is a mathematical technique used to mitigate rounding and measurement errors in mathematical computation by computing function bounds. Numerical methods involving interval arithmetic can guarantee relatively reliable and mathematically correct results. Instead of representing a value as a single number, interval arithmetic or interval mathematics represents each value as a range of possibilities. Mathematically, instead of working with an uncertain real-valued variable x, interval arithmetic works with an interval ,b/math> that defines the range of values that x can have. In other words, any value of the variable x lies in the closed interval between a and b. A function f, when applied to x, produces an interval ,d/math> which includes all the possible values for f(x) for all x \in ,b/math>. Interval arithmetic is suitable for a variety of purposes; the most common use is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer-assisted Proof
Automation describes a wide range of technologies that reduce human intervention in processes, mainly by predetermining decision criteria, subprocess relationships, and related actions, as well as embodying those predeterminations in machines. Automation has been achieved by various means including mechanical, hydraulic, pneumatic, electrical, electronic devices, and computers, usually in combination. Complicated systems, such as modern factories, airplanes, and ships typically use combinations of all of these techniques. The benefit of automation includes labor savings, reducing waste, savings in electricity costs, savings in material costs, and improvements to quality, accuracy, and precision. Automation includes the use of various equipment and control systems such as machinery, processes in factories, boilers, and heat-treating ovens, switching on telephone networks, steering, stabilization of ships, aircraft and other applications and vehicles with reduced human ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Julia (programming Language)
Julia is a high-level programming language, high-level, general-purpose programming language, general-purpose dynamic programming language, dynamic programming language, designed to be fast and productive, for e.g. data science, artificial intelligence, machine learning, modeling and simulation, most commonly used for numerical analysis and computational science. Distinctive aspects of Julia's design include a type system with parametric polymorphism and the use of multiple dispatch as a core programming paradigm, a default just-in-time compilation, just-in-time (JIT) compiler (with support for ahead-of-time compilation) and an tracing garbage collection, efficient (multi-threaded) garbage collection implementation. Notably Julia does not support classes with encapsulated methods and instead it relies on structs with generic methods/functions not tied to them. By default, Julia is run similarly to scripting languages, using its runtime, and allows for read–eval–print loop, i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
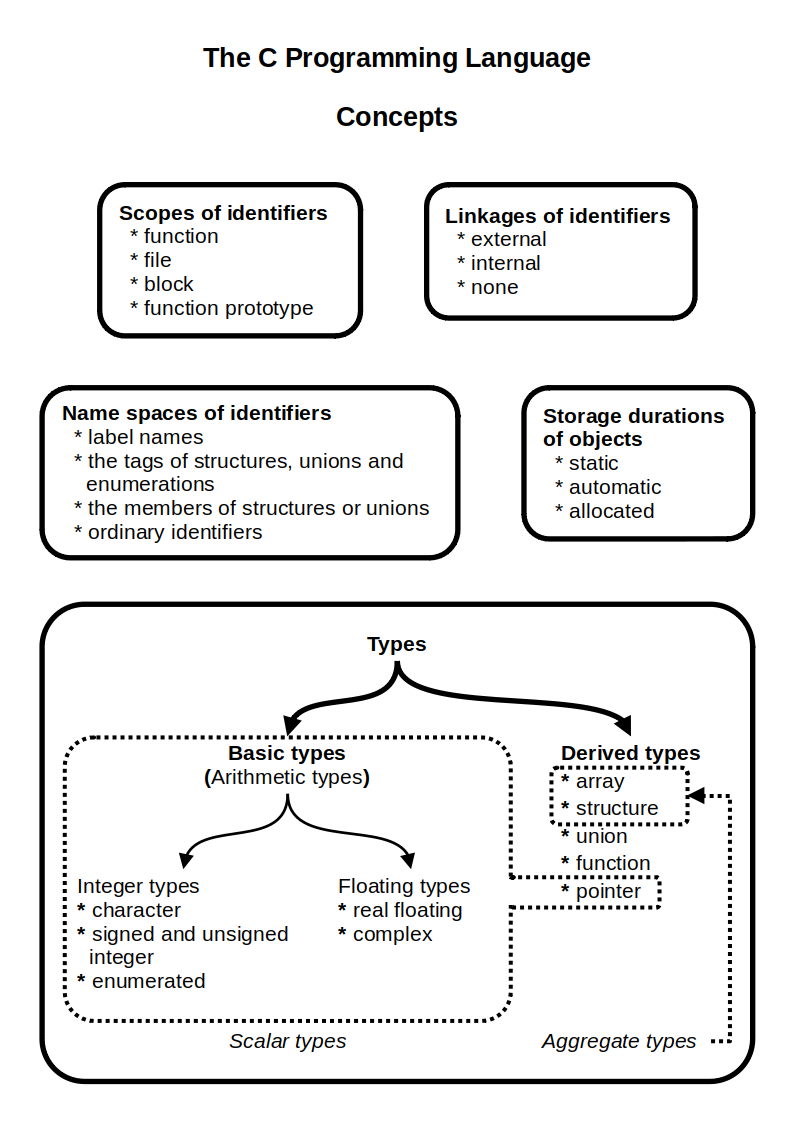
C (programming Language)
C (''pronounced'' '' – like the letter c'') is a general-purpose programming language. It was created in the 1970s by Dennis Ritchie and remains very widely used and influential. By design, C's features cleanly reflect the capabilities of the targeted Central processing unit, CPUs. It has found lasting use in operating systems code (especially in Kernel (operating system), kernels), device drivers, and protocol stacks, but its use in application software has been decreasing. C is commonly used on computer architectures that range from the largest supercomputers to the smallest microcontrollers and embedded systems. A successor to the programming language B (programming language), B, C was originally developed at Bell Labs by Ritchie between 1972 and 1973 to construct utilities running on Unix. It was applied to re-implementing the kernel of the Unix operating system. During the 1980s, C gradually gained popularity. It has become one of the most widely used programming langu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
GNU MPFR
The GNU Multiple Precision Floating-Point Reliable Library (GNU MPFR) is a GNU portable C library for arbitrary-precision binary floating-point computation with correct rounding, based on GNU Multi-Precision Library. Library MPFR's computation is both efficient and has a well-defined semantics: the functions are completely specified on all the possible operands and the results do not depend on the platform. This is done by copying the ideas from the ANSI/IEEE-754 standard for fixed-precision floating-point arithmetic (correct rounding and exceptions, in particular). More precisely, its main features are: * Support for special numbers: signed zeros (+0 and −0), infinities and not-a-number (a single NaN is supported: MPFR does not differentiate between quiet NaNs and signaling NaNs). * Each number has its own precision (in bits since MPFR uses radix 2). The floating-point results are correctly rounded to the precision of the target variable, in one of the five supported rou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
GNU Octave
GNU Octave is a scientific programming language for scientific computing and numerical computation. Octave helps in solving linear and nonlinear problems numerically, and for performing other numerical experiments using a language that is mostly compatible with MATLAB. It may also be used as a Batch processing, batch-oriented language. As part of the GNU Project, it is free software under the terms of the GNU General Public License. History The project was conceived around 1988. At first it was intended to be a companion to a chemical reactor design course. Full development was started by John W. Eaton in 1992. The first alpha release dates back to 4 January 1993 and on 17 February 1994 version 1.0 was released. Version 9.2.0 was released on 7 June 2024. The program is named after Octave Levenspiel, a former professor of the principal author. Levenspiel was known for his ability to perform quick back-of-the-envelope calculations. Development history Developments In addition ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MATLAB
MATLAB (an abbreviation of "MATrix LABoratory") is a proprietary multi-paradigm programming language and numeric computing environment developed by MathWorks. MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages. Although MATLAB is intended primarily for numeric computing, an optional toolbox uses the MuPAD symbolic engine allowing access to symbolic computing abilities. An additional package, Simulink, adds graphical multi-domain simulation and model-based design for dynamic and embedded systems. , MATLAB has more than four million users worldwide. They come from various backgrounds of engineering, science, and economics. , more than 5000 global colleges and universities use MATLAB to support instruction and research. History Origins MATLAB was invented by mathematician and computer programmer Cleve Moler. The idea for MATLAB was base ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |