|
Varignon Frame
The Varignon frame, named after Pierre Varignon, is a mechanical device which can be used to determine an optimal location of a warehouse for the destribution of goods to a set of shops. Optimal means that the sum of the ''weighted distances'' of the shops to the warehouse should be minimal. The frame consists of a board with n holes corresponding to the n shops at the locations \mathbf x_1, ...\mathbf x_n, n strings are tied together in a knot at one end, the loose ends are passed, one each, through the holes and are attached to weights below the board (see diagram). If the influence of friction and other odds of the real world are neglected, the knot will take a position of equilibrium \mathbf v. It can be shown (see below), that point \mathbf v is the optimal location which minimizes the weighted sum of distances :(1): \ D(\mathbf x)=\sum_^n m_i\, \mathbf x_i-\mathbf x\, . The optimization problem is called Weber problem. Mechanical Problem - Optimization Problem If the holes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Varignon's Theorem
Varignon's theorem is a statement in Euclidean geometry, that deals with the construction of a particular parallelogram, the Varignon parallelogram, from an arbitrary quadrilateral (quadrangle). It is named after Pierre Varignon, whose proof was published posthumously in 1731. Theorem The midpoints of the sides of an arbitrary quadrilateral form a parallelogram. If the quadrilateral is convex or concave (not complex), then the area of the parallelogram is half the area of the quadrilateral. If one introduces the concept of oriented areas for ''n''-gons, then this area equality also holds for complex quadrilaterals. Coxeter, H. S. M. and Greitzer, S. L. "Quadrangle; Varignon's theorem" §3.1 in Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 52–54, 1967. The Varignon parallelogram exists even for a skew quadrilateral, and is planar whether the quadrilateral is planar or not. The theorem can be generalized to the midpoint polygon of an arbitrary polygon. Proof ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermat Point
In Euclidean geometry, the Fermat point of a triangle, also called the Torricelli point or Fermat–Torricelli point, is a point such that the sum of the three distances from each of the three vertices of the triangle to the point is the smallest possible. It is so named because this problem was first raised by Fermat in a private letter to Evangelista Torricelli, who solved it. The Fermat point gives a solution to the geometric median and Steiner tree problems for three points. Construction The Fermat point of a triangle with largest angle at most 120° is simply its first isogonic center or X(13), which is constructed as follows: # Construct an equilateral triangle on each of two arbitrarily chosen sides of the given triangle. # Draw a line from each new vertex to the opposite vertex of the original triangle. # The two lines intersect at the Fermat point. An alternative method is the following: # On each of two arbitrarily chosen sides, construct an isosceles triangle, with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fixed Point (mathematics)
A fixed point (sometimes shortened to fixpoint, also known as an invariant point) is a value that does not change under a given transformation. Specifically, in mathematics, a fixed point of a function is an element that is mapped to itself by the function. In physics, the term fixed point can refer to a temperature that can be used as a reproducible reference point, usually defined by a phase change or triple point. Fixed point of a function Formally, is a fixed point of a function if belongs to both the domain and the codomain of , and . For example, if is defined on the real numbers by f(x) = x^2 - 3 x + 4, then 2 is a fixed point of , because . Not all functions have fixed points: for example, , has no fixed points, since is never equal to for any real number. In graphical terms, a fixed point means the point is on the line , or in other words the graph of has a point in common with that line. Fixed-point iteration In numerical analysis, ''fixed-point iter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weiszfeld Algorithm
In geometry, the geometric median of a discrete set of sample points in a Euclidean space is the point minimizing the sum of distances to the sample points. This generalizes the median, which has the property of minimizing the sum of distances for one-dimensional data, and provides a central tendency in higher dimensions. It is also known as the 1-median, spatial median, Euclidean minisum point, or Torricelli point. The geometric median is an important estimator of location in statistics, where it is also known as the ''L''1 estimator. It is also a standard problem in facility location, where it models the problem of locating a facility to minimize the cost of transportation. The special case of the problem for three points in the plane (that is, = 3 and = 2 in the definition below) is sometimes also known as Fermat's problem; it arises in the construction of minimal Steiner trees, and was originally posed as a problem by Pierre de Fermat and solved by Evangelista Torricelli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
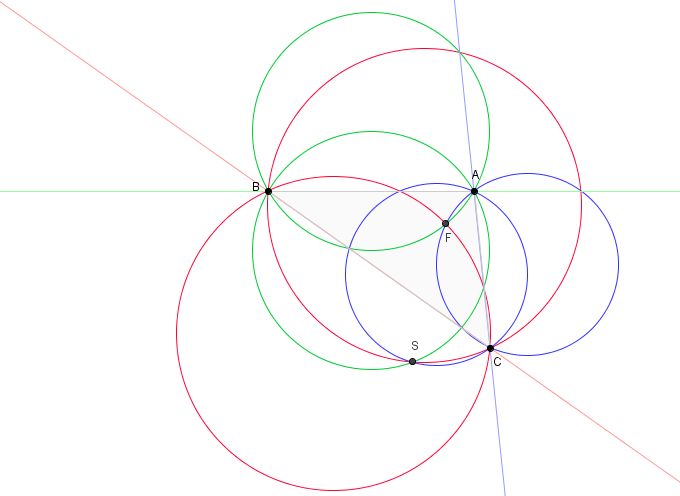
Confocal Conic Sections
In geometry, two conic sections are called confocal, if they have the same foci. Because ellipses and hyperbolas possess two foci, there are confocal ellipses, confocal hyperbolas and confocal mixtures of ellipses and hyperbolas. In the mixture of confocal ellipses and hyperbolas, any ellipse intersects any hyperbola orthogonally (at right angles). Parabolas possess only one focus, so, by convention, confocal parabolas have the same focus ''and'' the same axis of symmetry. Consequently, any point not on the axis of symmetry lies on two confocal parabolas which intersect orthogonally (see below). The formal extension of the concept of confocal conics to surfaces leads to confocal quadrics. Confocal ellipses An ellipse which is not a circle is uniquely determined by its foci F_1,\; F_2 and a point not on the major axis (see the definition of an ellipse as a locus of points). The pencil of confocal ellipses with the foci F_1=(c,0),\; F_2=(-c,0) can be described by the equation * \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Implicit Curve
In mathematics, an implicit curve is a plane curve defined by an implicit equation relating two coordinate variables, commonly ''x'' and ''y''. For example, the unit circle is defined by the implicit equation x^2+y^2=1. In general, every implicit curve is defined by an equation of the form : F(x,y)=0 for some function ''F'' of two variables. Hence an implicit curve can be considered as the set of zeros of a function of two variables. ''Implicit'' means that the equation is not expressed as a solution for either ''x'' in terms of ''y'' or vice versa. If F(x,y) is a polynomial in two variables, the corresponding curve is called an ''algebraic curve'', and specific methods are available for studying it. Plane curves can be represented in Cartesian coordinates (''x'', ''y'' coordinates) by any of three methods, one of which is the implicit equation given above. The graph of a function is usually described by an equation y=f(x) in which the functional form is explicitly stated; t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pierre Varignon
Pierre Varignon (1654 – 23 December 1722) was a French mathematician. He was educated at the Jesuit College and the University of Caen, where he received his M.A. in 1682. He took Holy Orders the following year. Varignon gained his first exposure to mathematics by reading Euclid and then Descartes' ''La Géométrie''. He became professor of mathematics at the Collège Mazarin in Paris in 1688 and was elected to the Académie Royale des Sciences in the same year. In 1704 he held the departmental chair at Collège Mazarin and also became professor of mathematics at the Collège Royal. He was elected to the Berlin Academy in 1713 and to the Royal Society in 1718. Many of his works were published in Paris in 1725, three years after his death. His lectures at Mazarin were published in Elements de mathematique' in 1731. Varignon was a friend of Newton, Leibniz, and the Bernoulli family. Varignon's principal contributions were to graphic statics and mechanics. Except for l'H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Level Set
In mathematics, a level set of a real-valued function of real variables is a set where the function takes on a given constant value , that is: : L_c(f) = \left\~, When the number of independent variables is two, a level set is called a level curve, also known as ''contour line'' or ''isoline''; so a level curve is the set of all real-valued solutions of an equation in two variables and . When , a level set is called a level surface (or ''isosurface''); so a level surface is the set of all real-valued roots of an equation in three variables , and . For higher values of , the level set is a level hypersurface, the set of all real-valued roots of an equation in variables. A level set is a special case of a fiber. Alternative names Level sets show up in many applications, often under different names. For example, an implicit curve is a level curve, which is considered independently of its neighbor curves, emphasizing that such a curve is defined by an implicit e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |