|
Upper Convected Time Derivative
In continuum mechanics, including fluid dynamics, an upper-convected time derivative or Oldroyd derivative, named after James G. Oldroyd, is the rate of change of some tensor property of a small parcel of fluid that is written in the coordinate system rotating and stretching with the fluid. The operator is specified by the following formula: : \stackrel = \frac \mathbf - (\nabla \mathbf)^T \cdot \mathbf - \mathbf \cdot (\nabla \mathbf) where: * is the upper-convected time derivative of a tensor field \mathbf *\frac is the substantive derivative *\nabla \mathbf=\frac is the tensor of velocity derivatives for the fluid. The formula can be rewritten as: : _ = \frac + v_k \frac - \frac A_ - \frac A_ By definition, the upper-convected time derivative of the Finger tensor is always zero. It can be shown that the upper-convected time derivative of a spacelike vector field is just its Lie derivative by the velocity field of the continuum. The upper-convected derivative ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuum Mechanics
Continuum mechanics is a branch of mechanics that deals with the mechanical behavior of materials modeled as a continuous mass rather than as discrete particles. The French mathematician Augustin-Louis Cauchy was the first to formulate such models in the 19th century. Explanation A continuum model assumes that the substance of the object fills the space it occupies. Modeling objects in this way ignores the fact that matter is made of atoms, and so is not continuous; however, on length scales much greater than that of inter-atomic distances, such models are highly accurate. These models can be used to derive differential equations that describe the behavior of such objects using physical laws, such as mass conservation, momentum conservation, and energy conservation, and some information about the material is provided by constitutive relationships. Continuum mechanics deals with the physical properties of solids and fluids which are independent of any particular coordinate sy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
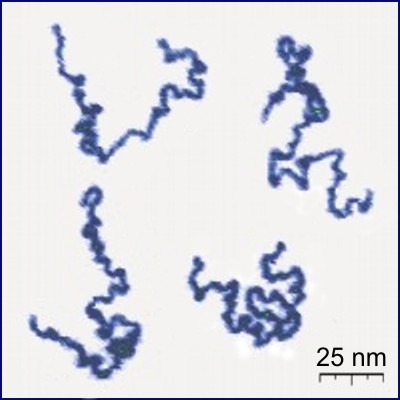
Polymer
A polymer (; Greek '' poly-'', "many" + ''-mer'', "part") is a substance or material consisting of very large molecules called macromolecules, composed of many repeating subunits. Due to their broad spectrum of properties, both synthetic and natural polymers play essential and ubiquitous roles in everyday life. Polymers range from familiar synthetic plastics such as polystyrene to natural biopolymers such as DNA and proteins that are fundamental to biological structure and function. Polymers, both natural and synthetic, are created via polymerization of many small molecules, known as monomers. Their consequently large molecular mass, relative to small molecule compounds, produces unique physical properties including toughness, high elasticity, viscoelasticity, and a tendency to form amorphous and semicrystalline structures rather than crystals. The term "polymer" derives from the Greek word πολύς (''polus'', meaning "many, much") and μέρος (''meros'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivariable Calculus
Multivariable calculus (also known as multivariate calculus) is the extension of calculus in one variable to calculus with functions of several variables: the differentiation and integration of functions involving several variables, rather than just one. Multivariable calculus may be thought of as an elementary part of advanced calculus. For advanced calculus, see calculus on Euclidean space. The special case of calculus in three dimensional space is often called vector calculus. Typical operations Limits and continuity A study of limits and continuity in multivariable calculus yields many counterintuitive results not demonstrated by single-variable functions. For example, there are scalar functions of two variables with points in their domain which give different limits when approached along different paths. E.g., the function. :f(x,y) = \frac approaches zero whenever the point (0,0) is approached along lines through the origin (y=kx). However, when the origin is appr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Upper-convected Maxwell Model
The upper-convected Maxwell (UCM) model is a generalisation of the Maxwell material for the case of large deformations using the upper-convected time derivative. The model was proposed by James G. Oldroyd. The concept is named after James Clerk Maxwell. The model can be written as: : \mathbf + \lambda \stackrel = 2\eta_0 \mathbf where: * \mathbf is the stress tensor; * \lambda is the relaxation time; * \stackrel is the upper-convected time derivative of stress tensor: : \stackrel = \frac \mathbf + \mathbf \cdot \nabla \mathbf - (\nabla \mathbf)^T \cdot \mathbf - \mathbf \cdot (\nabla \mathbf) *\mathbf is the fluid velocity *\eta_0 is material viscosity at steady simple shear; *\mathbf is the deformation rate tensor. Case of the steady shear For this case only two components of the shear stress became non-zero: :T_=\eta_0 \dot \gamma \, and :T_=2 \eta_0 \lambda ^2 \, where \dot \gamma is the shear rate. Thus, the upper-convected Maxwell model predicts for the simple shear ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simple Shear
Simple shear is a deformation in which parallel planes in a material remain parallel and maintain a constant distance, while translating relative to each other. In fluid mechanics In fluid mechanics, simple shear is a special case of deformation where only one component of velocity vectors has a non-zero value: :V_x=f(x,y) :V_y=V_z=0 And the gradient of velocity is constant and perpendicular to the velocity itself: :\frac = \dot \gamma , where \dot \gamma is the shear rate and: :\frac = \frac = 0 The displacement gradient tensor Γ for this deformation has only one nonzero term: :\Gamma = \begin 0 & & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end Simple shear with the rate \dot \gamma is the combination of pure shear strain with the rate of \dot \gamma and rotation with the rate of \dot \gamma: :\Gamma = \begin \underbrace \begin 0 & & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end \\ \mbox\end = \begin \underbrace \begin 0 & & 0 \\ & 0 & 0 \\ 0 & 0 & 0 \end \\ \mbox \end + \begi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simple Shear
Simple shear is a deformation in which parallel planes in a material remain parallel and maintain a constant distance, while translating relative to each other. In fluid mechanics In fluid mechanics, simple shear is a special case of deformation where only one component of velocity vectors has a non-zero value: :V_x=f(x,y) :V_y=V_z=0 And the gradient of velocity is constant and perpendicular to the velocity itself: :\frac = \dot \gamma , where \dot \gamma is the shear rate and: :\frac = \frac = 0 The displacement gradient tensor Γ for this deformation has only one nonzero term: :\Gamma = \begin 0 & & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end Simple shear with the rate \dot \gamma is the combination of pure shear strain with the rate of \dot \gamma and rotation with the rate of \dot \gamma: :\Gamma = \begin \underbrace \begin 0 & & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end \\ \mbox\end = \begin \underbrace \begin 0 & & 0 \\ & 0 & 0 \\ 0 & 0 & 0 \end \\ \mbox \end + \begi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Tensor
In mathematics, a symmetric tensor is a tensor that is invariant under a permutation of its vector arguments: :T(v_1,v_2,\ldots,v_r) = T(v_,v_,\ldots,v_) for every permutation ''σ'' of the symbols Alternatively, a symmetric tensor of order ''r'' represented in coordinates as a quantity with ''r'' indices satisfies :T_ = T_. The space of symmetric tensors of order ''r'' on a finite-dimensional vector space ''V'' is naturally isomorphic to the dual of the space of homogeneous polynomials of degree ''r'' on ''V''. Over fields of characteristic zero, the graded vector space of all symmetric tensors can be naturally identified with the symmetric algebra on ''V''. A related concept is that of the antisymmetric tensor or alternating form. Symmetric tensors occur widely in engineering, physics and mathematics. Definition Let ''V'' be a vector space and :T\in V^ a tensor of order ''k''. Then ''T'' is a symmetric tensor if :\tau_\sigma T = T\, for the braiding maps associated to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Viscoelastic
In materials science and continuum mechanics, viscoelasticity is the property of materials that exhibit both viscous and elastic characteristics when undergoing deformation. Viscous materials, like water, resist shear flow and strain linearly with time when a stress is applied. Elastic materials strain when stretched and immediately return to their original state once the stress is removed. Viscoelastic materials have elements of both of these properties and, as such, exhibit time-dependent strain. Whereas elasticity is usually the result of bond stretching along crystallographic planes in an ordered solid, viscosity is the result of the diffusion of atoms or molecules inside an amorphous material.Meyers and Chawla (1999): "Mechanical Behavior of Materials", 98-103. Background In the nineteenth century, physicists such as Maxwell, Boltzmann, and Kelvin researched and experimented with creep and recovery of glasses, metals, and rubbers. Viscoelasticity was further examined in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rheology
Rheology (; ) is the study of the flow of matter, primarily in a fluid ( liquid or gas) state, but also as "soft solids" or solids under conditions in which they respond with plastic flow rather than deforming elastically in response to an applied force. Rheology is a branch of physics, and it is the science that deals with the deformation and flow of materials, both solids and liquids.W. R. Schowalter (1978) Mechanics of Non-Newtonian Fluids Pergamon The term ''rheology'' was coined by Eugene C. Bingham, a professor at Lafayette College, in 1920, from a suggestion by a colleague, Markus Reiner.The Deborah Number The term was inspired by the of |
Lie Derivative
In differential geometry, the Lie derivative ( ), named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a tensor field (including scalar functions, vector fields and one-forms), along the flow defined by another vector field. This change is coordinate invariant and therefore the Lie derivative is defined on any differentiable manifold. Functions, tensor fields and forms can be differentiated with respect to a vector field. If ''T'' is a tensor field and ''X'' is a vector field, then the Lie derivative of ''T'' with respect to ''X'' is denoted \mathcal_X(T). The differential operator T \mapsto \mathcal_X(T) is a derivation of the algebra of tensor fields of the underlying manifold. The Lie derivative commutes with contraction and the exterior derivative on differential forms. Although there are many concepts of taking a derivative in differential geometry, they all agree when the expression being differentiated is a function or scalar field. Thus in t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Dynamics
In physics and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids— liquids and gases. It has several subdisciplines, including ''aerodynamics'' (the study of air and other gases in motion) and hydrodynamics (the study of liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moments on aircraft, determining the mass flow rate of petroleum through pipelines, predicting weather patterns, understanding nebulae in interstellar space and modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fluid dynamics problem typically involves the calculation of various properties of the fluid, such as flow velocity, pressure, density, and temperature, as functions of space and time. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finger Tensor
In continuum mechanics, the finite strain theory—also called large strain theory, or large deformation theory—deals with deformations in which strains and/or rotations are large enough to invalidate assumptions inherent in infinitesimal strain theory. In this case, the undeformed and deformed configurations of the continuum are significantly different, requiring a clear distinction between them. This is commonly the case with elastomers, plastically-deforming materials and other fluids and biological soft tissue. Displacement The displacement of a body has two components: a rigid-body displacement and a deformation. * A rigid-body displacement consists of a simultaneous translation (physics) and rotation of the body without changing its shape or size. * Deformation implies the change in shape and/or size of the body from an initial or undeformed configuration \kappa_0(\mathcal B) to a current or deformed configuration \kappa_t(\mathcal B) (Figure 1). A change in the c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
(y))⁄((x^4) (y^2)).png)