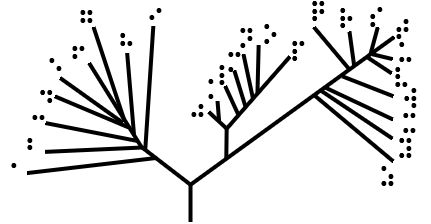
|
Unrooted Binary Tree
In mathematics and computer science, an unrooted binary tree is an unrooted tree in which each vertex has either one or three neighbors. Definitions A free tree or unrooted tree is a connected undirected graph with no cycles. The vertices with one neighbor are the ''leaves'' of the tree, and the remaining vertices are the ''internal nodes'' of the tree. The degree of a vertex is its number of neighbors; in a tree with more than one node, the leaves are the vertices of degree one. An unrooted binary tree is a free tree in which all internal nodes have degree exactly three. In some applications it may make sense to distinguish subtypes of unrooted binary trees: a planar embedding of the tree may be fixed by specifying a cyclic ordering for the edges at each vertex, making it into a plane tree. In computer science, binary trees are often rooted and ordered when they are used as data structures, but in the applications of unrooted binary trees in hierarchical clustering and evolutiona ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phylogenetic Tree
A phylogenetic tree (also phylogeny or evolutionary tree Felsenstein J. (2004). ''Inferring Phylogenies'' Sinauer Associates: Sunderland, MA.) is a branching diagram or a tree showing the evolutionary relationships among various biological species or other entities based upon similarities and differences in their physical or genetic characteristics. All life on Earth is part of a single phylogenetic tree, indicating common ancestry. In a ''rooted'' phylogenetic tree, each node with descendants represents the inferred most recent common ancestor of those descendants, and the edge lengths in some trees may be interpreted as time estimates. Each node is called a taxonomic unit. Internal nodes are generally called hypothetical taxonomic units, as they cannot be directly observed. Trees are useful in fields of biology such as bioinformatics, systematics, and phylogenetics. ''Unrooted'' trees illustrate only the relatedness of the leaf nodes and do not require the ancestral root to b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kraft–McMillan Inequality
In coding theory, the Kraft–McMillan inequality gives a necessary and sufficient condition for the existence of a prefix code (in Leon G. Kraft's version) or a uniquely decodable code (in Brockway McMillan's version) for a given set of codeword lengths. Its applications to prefix codes and trees often find use in computer science and information theory. Kraft's inequality was published in . However, Kraft's paper discusses only prefix codes, and attributes the analysis leading to the inequality to Raymond Redheffer. The result was independently discovered in . McMillan proves the result for the general case of uniquely decodable codes, and attributes the version for prefix codes to a spoken observation in 1955 by Joseph Leo Doob. Applications and intuitions Kraft's inequality limits the lengths of codewords in a prefix code: if one takes an exponential of the length of each valid codeword, the resulting set of values must look like a probability mass function, that is, it must ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laurence Wolsey
Laurence Alexander Wolsey is an English mathematician working in the field of integer programming. He is a former president and research director of the Center for Operations Research and Econometrics (CORE) at Université catholique de Louvain in Belgium. He is professor emeritus of applied mathematics at the engineering school of the same university. Early life and education Wolsey received a MSc in Mathematics from Cambridge in 1966 and a Ph.D. in Mathematics from the Massachusetts Institute of Technology in 1969 under the supervision of Jeremy F. Shapiro. Career Wolsey was visiting researcher at the Manchester Business School in 1969–1971. He was invited by George L. Nemhauser as a Post-Doctoral student to CORE in Belgium in 1971. He met his future wife, Marguerite Loute, sister of CORE colleague Etienne Loute, and settled in Belgium. He was later a visiting professor at the London School of Economics in 1978–1979, at Cornell University in 1983, at Ecole polytechnique d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Raffaele Pesenti
Raffaele () is an Italian given name and surname, variant of the English Raphael. Notable people with the name include: Given name *Raffaele Amato, Italian mobster *Raffaele Cutolo, Italian mobster *Raffaele Ganci, Italian mobster *Raffaele Cantone, Italian magistrate *Raffaele De Rosa, Italian motorcycle racer * Raffaele Di Paco, Italian cyclist *Raffaele Fitto, Italian politician *Raffaele Guariglia, Italian politician *Raffaele Lombardo, Italian politician *Raffaele Palladino, Italian footballer *Raffaele Pinto, Italian racing driver *Raffaele Pisu, Italiano actor *Raffaele Riario, Italian cardinal *Raffaele Rossetti, Italian politician *Raffaele Carlo Rossi, Italian cardinal *Raffaele Viviani, Italian artist *Raffaele Contigiani (1920–2008), Italian architect Surname * Virginia Raffaele, Italian actress See also * Raphael (other) * Rafael (other) * San Raffaele (other) * Raffaello (other) Raffaello, Raffaele or Raffaellino is an Italian ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
An Example Of An Unrooted Binary Tree With Four Leaves
An, AN, aN, or an may refer to: Businesses and organizations * Airlinair (IATA airline code AN) * Alleanza Nazionale, a former political party in Italy * AnimeNEXT, an annual anime convention located in New Jersey * Anime North, a Canadian anime convention * Ansett Australia, a major Australian airline group that is now defunct (IATA designator AN) * Apalachicola Northern Railroad (reporting mark AN) 1903–2002 ** AN Railway, a successor company, 2002– * Aryan Nations, a white supremacist religious organization * Australian National Railways Commission, an Australian rail operator from 1975 until 1987 * Antonov, a Ukrainian (formerly Soviet) aircraft manufacturing and services company, as a model prefix Entertainment and media * Antv, an Indonesian television network * ''Astronomische Nachrichten'', or ''Astronomical Notes'', an international astronomy journal * ''Avisa Nordland'', a Norwegian newspaper * ''Sweet Bean'' (あん), a 2015 Japanese film also known as ''An'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Double Factorial
In mathematics, the double factorial or semifactorial of a number , denoted by , is the product of all the integers from 1 up to that have the same parity (odd or even) as . That is, :n!! = \prod_^ (n-2k) = n (n-2) (n-4) \cdots. For even , the double factorial is :n!! = \prod_^\frac (2k) = n(n-2)(n-4)\cdots 4\cdot 2 \,, and for odd it is :n!! = \prod_^\frac (2k-1) = n(n-2)(n-4)\cdots 3\cdot 1 \,. For example, . The zero double factorial as an empty product. The sequence of double factorials for even = starts as : 1, 2, 8, 48, 384, 3840, 46080, 645120,... The sequence of double factorials for odd = starts as : 1, 3, 15, 105, 945, 10395, 135135,... The term odd factorial is sometimes used for the double factorial of an odd number. History and usage In a 1902 paper, the physicist Arthur Schuster wrote: states that the double factorial was originally introduced in order to simplify the expression of certain trigonometric integrals that arise in the derivation of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Enumeration
In combinatorics, an area of mathematics, graph enumeration describes a class of combinatorial enumeration problems in which one must count undirected or directed graphs of certain types, typically as a function of the number of vertices of the graph. These problems may be solved either exactly (as an algebraic enumeration problem) or asymptotically. The pioneers in this area of mathematics were George Pólya, Arthur Cayley and J. Howard Redfield. Labeled vs unlabeled problems In some graphical enumeration problems, the vertices of the graph are considered to be ''labeled'' in such a way as to be distinguishable from each other, while in other problems any permutation of the vertices is considered to form the same graph, so the vertices are considered identical or ''unlabeled''. In general, labeled problems tend to be easier. As with combinatorial enumeration more generally, the Pólya enumeration theorem is an important tool for reducing unlabeled problems to labeled ones: each ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamic Programming
Dynamic programming is both a mathematical optimization method and a computer programming method. The method was developed by Richard Bellman in the 1950s and has found applications in numerous fields, from aerospace engineering to economics. In both contexts it refers to simplifying a complicated problem by breaking it down into simpler sub-problems in a recursive manner. While some decision problems cannot be taken apart this way, decisions that span several points in time do often break apart recursively. Likewise, in computer science, if a problem can be solved optimally by breaking it into sub-problems and then recursively finding the optimal solutions to the sub-problems, then it is said to have ''optimal substructure''. If sub-problems can be nested recursively inside larger problems, so that dynamic programming methods are applicable, then there is a relation between the value of the larger problem and the values of the sub-problems.Cormen, T. H.; Leiserson, C. E.; Rives ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Treewidth
In graph theory, the treewidth of an undirected graph is an integer number which specifies, informally, how far the graph is from being a tree. The smallest treewidth is 1; the graphs with treewidth 1 are exactly the trees and the forests. The graphs with treewidth at most 2 are the series–parallel graphs. The maximal graphs with treewidth exactly are called '' -trees'', and the graphs with treewidth at most are called '' partial -trees''. Many other well-studied graph families also have bounded treewidth. Treewidth may be formally defined in several equivalent ways: in terms of the size of the largest vertex set in a tree decomposition of the graph, in terms of the size of the largest clique in a chordal completion of the graph, in terms of the maximum order of a haven describing a strategy for a pursuit–evasion game on the graph, or in terms of the maximum order of a bramble, a collection of connected subgraphs that all touch each other. Treewidth is commonly used as a pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Branch-decomposition
In graph theory, a branch-decomposition of an undirected graph ''G'' is a hierarchical clustering of the edges of ''G'', represented by an unrooted binary tree ''T'' with the edges of ''G'' as its leaves. Removing any edge from ''T'' partitions the edges of ''G'' into two subgraphs, and the width of the decomposition is the maximum number of shared vertices of any pair of subgraphs formed in this way. The branchwidth of ''G'' is the minimum width of any branch-decomposition of ''G''. Branchwidth is closely related to tree-width: for all graphs, both of these numbers are within a constant factor of each other, and both quantities may be characterized by forbidden minors. And as with treewidth, many graph optimization problems may be solved efficiently for graphs of small branchwidth. However, unlike treewidth, the branchwidth of planar graphs may be computed exactly, in polynomial time. Branch-decompositions and branchwidth may also be generalized from graphs to matroids. Defin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quartet Distance
The quartet distance is a way of measuring the distance between two phylogenetic trees. It is defined as the number of subsets of four leaves that are not related by the same topology in both trees. Computing the quartet distance The most straightforward computation of the quartet distance would require O(N^4) time, where N is the number of leaves in the trees. For binary trees, better algorithm In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific problems or to perform a computation. Algorithms are used as specifications for performing ...s have been found to compute the distance in * O(N^2) time * O(N \log^2 N) time and * O(N \log N) time Gerth Stølting Brodal ''et al.'' found an algorithm that takes O(D N \log N) time to compute the quartet distance between two multifurcating trees when D is the maximum degree of the trees, which iaccessiblein C, perl, and the R packa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |