|
Tutte–Coxeter Graph
In the mathematics, mathematical field of graph theory, the Tutte–Coxeter graph or Tutte eight-cage or Cremona–Richmond graph is a 3-regular graph with 30 vertices and 45 edges. As the unique smallest cubic graph of girth (graph theory), girth 8, it is a cage (graph theory), cage and a Moore graph. It is bipartite graph, bipartite, and can be constructed as the Levi graph of the generalized quadrangle ''W''2 (known as the Cremona–Richmond configuration). The graph is named after William Thomas Tutte and H. S. M. Coxeter; it was discovered by Tutte (1947) but its connection to geometric configurations was investigated by both authors in a pair of jointly published papers (Tutte 1958; Coxeter 1958a). All the cubic graph, cubic distance-regular graphs are known. The Tutte–Coxeter is one of the 13 such graphs. It has Crossing number (graph theory), crossing number 13, book thickness 3 and queue number 2.Wolz, Jessica; ''Engineering Linear Layouts with SAT.'' Master Thesis, Un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Tutte Eight Cage
William Thomas Tutte (; 14 May 1917 – 2 May 2002) was an English and Canadian Cryptanalysis, code breaker and mathematician. During the Second World War, he made a fundamental advance in cryptanalysis of the Lorenz cipher, a major Nazi Germany, Nazi German cipher system which was used for top-secret communications within the Wehrmacht High Command. The high-level, strategic nature of the intelligence obtained from Tutte's crucial breakthrough, in the bulk decrypting of Lorenz-enciphered messages specifically, contributed greatly, and perhaps even decisively, to the defeat of Nazi Germany. He also had a number of significant mathematical accomplishments, including foundation work in the fields of graph theory and matroid theory. Tutte's research in the field of graph theory proved to be of remarkable importance. At a time when graph theory was still a primitive subject, Tutte commenced the study of matroids and developed them into a theory by expanding from the work that Hass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cremona–Richmond Configuration
In mathematics, the Cremona–Richmond configuration is a configuration of 15 lines and 15 points, having 3 points on each line and 3 lines through each point, and containing no triangles. It was studied by and . It is a generalized quadrangle with parameters (2,2). Its Levi graph is the Tutte–Coxeter graph. Symmetry The points of the Cremona–Richmond configuration may be identified with the 15=\tbinom unordered pairs of elements of a six-element set; these pairs are called ''duads''. Similarly, the lines of the configuration may be identified with the 15 ways of partitioning the same six elements into three pairs; these partitions are called ''synthemes''. Identified in this way, a point of the configuration is incident to a line of the configuration if and only if the duad corresponding to the point is one of the three pairs in the syntheme corresponding to the line. The symmetric group of all permutations of the six elements underlying this system of duads and synthemes ac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Building (mathematics)
In mathematics, a building (also Tits building, named after Jacques Tits) is a combinatorial and geometric structure which simultaneously generalizes certain aspects of flag manifolds, finite projective planes, and Riemannian symmetric spaces. Buildings were initially introduced by Jacques Tits as a means to understand the structure of Reductive group#Non-split reductive groups, isotropic Reductive group, reductive linear algebraic groups over arbitrary fields. The more specialized theory of Bruhat–Tits buildings (named also after François Bruhat) plays a role in the study of p-adic Lie group, -adic Lie groups analogous to that of the theory of symmetric spaces in the theory of Lie groups. Overview The notion of a building was invented by Jacques Tits as a means of describing group of Lie type, simple algebraic groups over an arbitrary field (mathematics), field. Tits demonstrated how to every such group (mathematics), group one can associate a simplicial complex with an Gr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
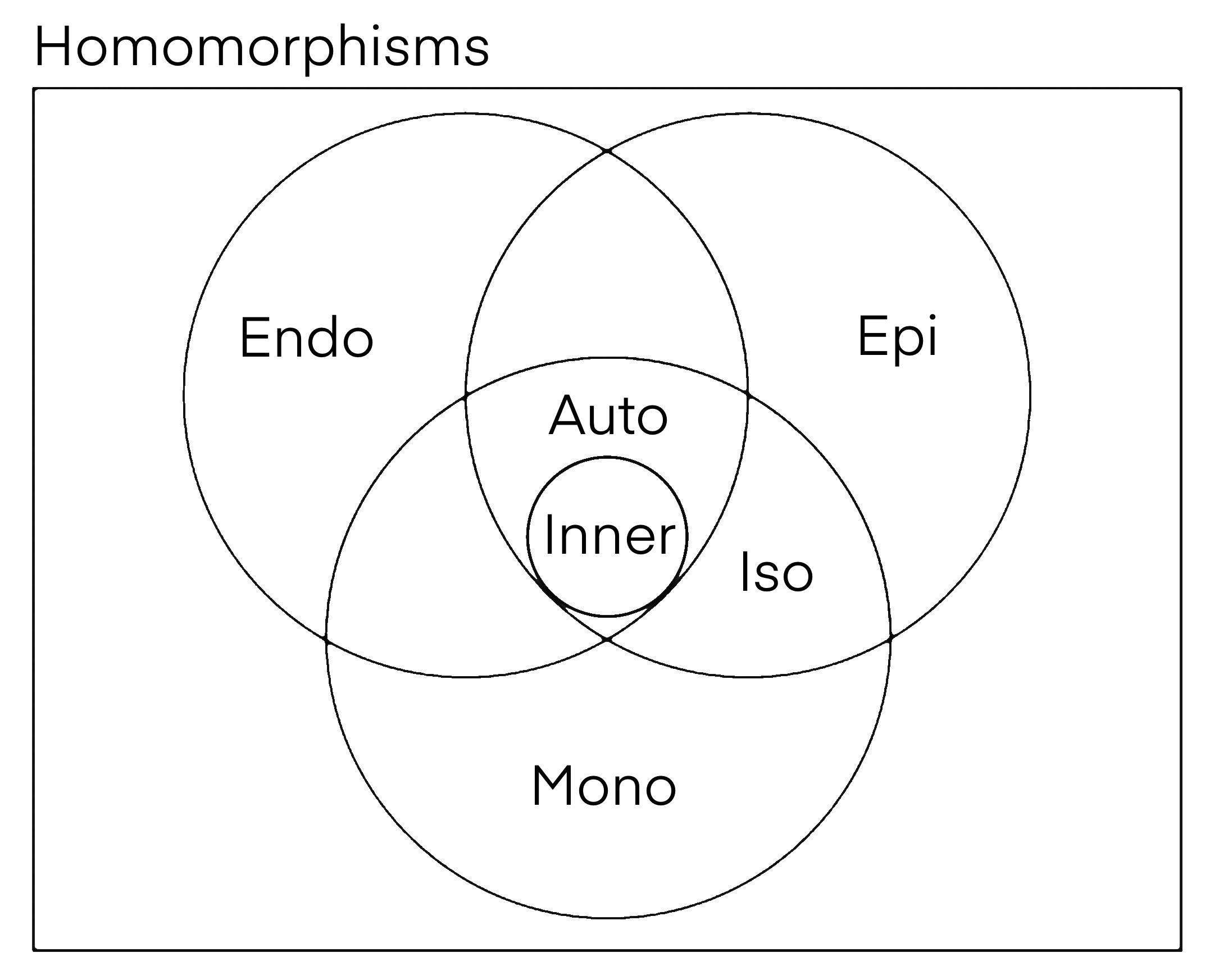
Outer Automorphism
In mathematics, the outer automorphism group of a group, , is the quotient, , where is the automorphism group of and ) is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted . If is trivial and has a trivial center, then is said to be complete. An automorphism of a group that is not inner is called an outer automorphism. The cosets of with respect to outer automorphisms are then the elements of ; this is an instance of the fact that quotients of groups are not, in general, (isomorphic to) subgroups. If the inner automorphism group is trivial (when a group is abelian), the automorphism group and outer automorphism group are naturally identified; that is, the outer automorphism group does act on the group. For example, for the alternating group, , the outer automorphism group is usually the group of order 2, with exceptions noted below. Considering as a subgroup of the symmetric group, , conjugation by any odd permutation is an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Inner Automorphism
In abstract algebra, an inner automorphism is an automorphism of a group, ring, or algebra Algebra is a branch of mathematics that deals with abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic ope ... given by the conjugation action of a fixed element, called the ''conjugating element''. They can be realized via operations from within the group itself, hence the adjective "inner". These inner automorphisms form a subgroup of the automorphism group, and the Quotient_group, quotient of the automorphism group by this subgroup is defined as the outer automorphism group. Definition If is a group and is an element of (alternatively, if is a ring, and is a Unit (ring theory), unit), then the function :\begin \varphi_g\colon G&\to G \\ \varphi_g(x)&:= g^xg \end is called (right) conjugation by (see also conjugacy class). This func ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Graph Automorphism
In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge– vertex connectivity. Formally, an automorphism of a graph is a permutation of the vertex set , such that the pair of vertices form an edge if and only if the pair also form an edge. That is, it is a graph isomorphism from to itself. Automorphisms may be defined in this way both for directed graphs and for undirected graphs. The composition of two automorphisms is another automorphism, and the set of automorphisms of a given graph, under the composition operation, forms a group, the automorphism group of the graph. In the opposite direction, by Frucht's theorem, all groups can be represented as the automorphism group of a connected graph – indeed, of a cubic graph. Computational complexity Constructing the automorphism group of a graph, in the form of a list of generators, is polynomial-time equivalent to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Group (mathematics)
In mathematics, a group is a Set (mathematics), set with an Binary operation, operation that combines any two elements of the set to produce a third element within the same set and the following conditions must hold: the operation is Associative property, associative, it has an identity element, and every element of the set has an inverse element. For example, the integers with the addition, addition operation form a group. The concept of a group was elaborated for handling, in a unified way, many mathematical structures such as numbers, geometric shapes and polynomial roots. Because the concept of groups is ubiquitous in numerous areas both within and outside mathematics, some authors consider it as a central organizing principle of contemporary mathematics. In geometry, groups arise naturally in the study of symmetries and geometric transformations: The symmetries of an object form a group, called the symmetry group of the object, and the transformations of a given type form a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Symmetric Graph
In the mathematical field of graph theory, a graph is symmetric or arc-transitive if, given any two ordered pairs of adjacent vertices (u_1,v_1) and (u_2,v_2) of , there is an automorphism :f : V(G) \rightarrow V(G) such that :f(u_1) = u_2 and f(v_1) = v_2. In other words, a graph is symmetric if its automorphism group acts transitively on ordered pairs of adjacent vertices (that is, upon edges considered as having a direction). Such a graph is sometimes also called -transitive or flag-transitive. By definition (ignoring and ), a symmetric graph without isolated vertices must also be vertex-transitive. Since the definition above maps one edge to another, a symmetric graph must also be edge-transitive. However, an edge-transitive graph need not be symmetric, since might map to , but not to . Star graphs are a simple example of being edge-transitive without being vertex-transitive or symmetric. As a further example, semi-symmetric graphs are edge-transitive and regular, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Incidence Structure
In mathematics, an incidence structure is an abstract system consisting of two types of objects and a single relationship between these types of objects. Consider the Point (geometry), points and Line (geometry), lines of the Euclidean plane as the two types of objects and ignore all the properties of this geometry except for the heterogeneous relation, relation of which points are incident (geometry), incident on which lines for all points and lines. What is left is the incidence structure of the Euclidean plane. Incidence structures are most often considered in the geometrical context where they are abstracted from, and hence generalize, planes (such as affine plane (incidence geometry), affine, projective plane, projective, and Möbius planes), but the concept is very broad and not limited to geometric settings. Even in a geometric setting, incidence structures are not limited to just points and lines; higher-dimensional objects (Plane (mathematics), planes, Solid geometry, sol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Complete Graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices is connected by a pair of unique edges (one in each direction). Graph theory itself is typically dated as beginning with Leonhard Euler's 1736 work on the Seven Bridges of Königsberg. However, drawings of complete graphs, with their vertices placed on the points of a regular polygon, had already appeared in the 13th century, in the work of Ramon Llull. Such a drawing is sometimes referred to as a mystic rose. Properties The complete graph on vertices is denoted by . Some sources claim that the letter in this notation stands for the German word , but the German name for a complete graph, , does not contain the letter , and other sources state that the notation honors the contributions of Kazimierz Kuratowski to graph theory. has edg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Perfect Matching
In graph theory, a perfect matching in a graph is a matching that covers every vertex of the graph. More formally, given a graph with edges and vertices , a perfect matching in is a subset of , such that every vertex in is adjacent to exactly one edge in . The adjacency matrix of a perfect matching is a symmetric permutation matrix. A perfect matching is also called a 1-factor; see Graph factorization for an explanation of this term. In some literature, the term complete matching is used. Every perfect matching is a maximum-cardinality matching, but the opposite is not true. For example, consider the following graphs:Alan Gibbons, Algorithmic Graph Theory, Cambridge University Press, 1985, Chapter 5. : In graph (b) there is a perfect matching (of size 3) since all 6 vertices are matched; in graphs (a) and (c) there is a maximum-cardinality matching (of size 2) which is not perfect, since some vertices are unmatched. A perfect matching is also a minimum-size edge cov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Queue Number
In the mathematical field of graph theory, the queue number of a Graph (discrete mathematics), graph is a graph invariant defined analogously to book thickness, stack number (book thickness) using Queue (abstract data type), first-in first-out (queue) orderings in place of Stack (abstract data type), last-in first-out (stack) orderings. Definition A queue layout of a given graph is defined by a total ordering of the vertex (graph theory), vertices of the graph together with a partition of the edge (graph theory), edges into a number of "queues". The set of edges in each queue is required to avoid edges that are properly nested: if and are two edges in the same queue, then it should not be possible to have in the vertex ordering. The queue number of a graph is the minimum number of queues in a queue layout.. Equivalently, from a queue layout, one could process the edges in a single queue using a Queue (abstract data type), queue data structure, by considering the vertices in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |