|
Torus (mathematics)
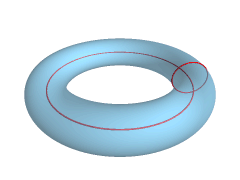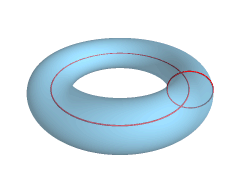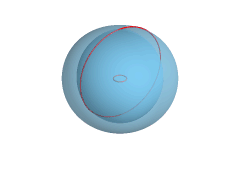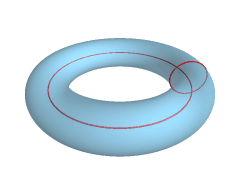
In geometry, a torus (plural tori, colloquially donut or doughnut) is a surface of revolution generated by revolving a circle in three-dimensional space about an axis that is coplanar with the circle. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a spindle torus. If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid. Real-world objects that approximate a torus of revolution include swim rings, inner tubes and ringette rings. Eyeglass lenses that combine spherical and cylindrical correction are toric lenses. A torus should not be confused with a ''solid torus'', which is formed by ro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torus
In geometry, a torus (plural tori, colloquially donut or doughnut) is a surface of revolution generated by revolving a circle in three-dimensional space about an axis that is coplanar with the circle. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a spindle torus. If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid. Real-world objects that approximate a torus of revolution include swim rings, inner tubes and ringette rings. Eyeglass lenses that combine spherical and cylindrical correction are toric lenses. A torus should not be confused with a '' solid torus'', which is formed by r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Disk (geometry)
In geometry, a disk (also spelled disc). is the region in a plane bounded by a circle. A disk is said to be ''closed'' if it contains the circle that constitutes its boundary, and ''open'' if it does not. For a radius, r, an open disk is usually denoted as D_r and a closed disk is \overline. However in the field of topology the closed disk is usually denoted as D^2 while the open disk is \operatorname D^2. Formulas In Cartesian coordinates, the ''open disk'' of center (a, b) and radius ''R'' is given by the formula :D=\ while the ''closed disk'' of the same center and radius is given by :\overline=\. The area of a closed or open disk of radius ''R'' is π''R''2 (see area of a disk). Properties The disk has circular symmetry. The open disk and the closed disk are not topologically equivalent (that is, they are not homeomorphic), as they have different topological properties from each other. For instance, every closed disk is compact whereas every open disk is not compact ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Genus (mathematics)
In mathematics, genus (plural genera) has a few different, but closely related, meanings. Intuitively, the genus is the number of "holes" of a surface. A sphere has genus 0, while a torus has genus 1. Topology Orientable surfaces The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It is equal to the number of handles on it. Alternatively, it can be defined in terms of the Euler characteristic ''χ'', via the relationship ''χ'' = 2 − 2''g'' for closed surfaces, where ''g'' is the genus. For surfaces with ''b'' boundary components, the equation reads ''χ'' = 2 − 2''g'' − ''b''. In layman's terms, it's the number of "holes" an object has ("holes" interpreted in the sense of doughnut holes; a hollow sphere would be considered as having zero holes in this sense). A torus has 1 such h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Four-dimensional Space
A four-dimensional space (4D) is a mathematical extension of the concept of three-dimensional or 3D space. Three-dimensional space is the simplest possible abstraction of the observation that one only needs three numbers, called ''dimensions'', to describe the sizes or locations of objects in the everyday world. For example, the volume of a rectangular box is found by measuring and multiplying its length, width, and height (often labeled ''x'', ''y'', and ''z''). The idea of adding a fourth dimension began with Jean le Rond d'Alembert's "Dimensions" being published in 1754, was followed by Joseph-Louis Lagrange in the mid-1700s, and culminated in a precise formalization of the concept in 1854 by Bernhard Riemann. In 1880, Charles Howard Hinton popularized these insights in an essay titled "What is the Fourth Dimension?", which explained the concept of a " four-dimensional cube" with a step-by-step generalization of the properties of lines, squares, and cubes. The simplest form ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clifford Torus
In geometric topology, the Clifford torus is the simplest and most symmetric flat embedding of the cartesian product of two circles ''S'' and ''S'' (in the same sense that the surface of a cylinder is "flat"). It is named after William Kingdon Clifford. It resides in R4, as opposed to in R3. To see why R4 is necessary, note that if ''S'' and ''S'' each exists in its own independent embedding space R and R, the resulting product space will be R4 rather than R3. The historically popular view that the cartesian product of two circles is an R3 torus in contrast requires the highly asymmetric application of a rotation operator to the second circle, since that circle will only have one independent axis ''z'' available to it after the first circle consumes ''x'' and ''y''. Stated another way, a torus embedded in R3 is an asymmetric reduced-dimension projection of the maximally symmetric Clifford torus embedded in R4. The relationship is similar to that of projecting the edges of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Embedding
In mathematics, an embedding (or imbedding) is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup. When some object X is said to be embedded in another object Y, the embedding is given by some injective and structure-preserving map f:X\rightarrow Y. The precise meaning of "structure-preserving" depends on the kind of mathematical structure of which X and Y are instances. In the terminology of category theory, a structure-preserving map is called a morphism. The fact that a map f:X\rightarrow Y is an embedding is often indicated by the use of a "hooked arrow" (); thus: f : X \hookrightarrow Y. (On the other hand, this notation is sometimes reserved for inclusion maps.) Given X and Y, several different embeddings of X in Y may be possible. In many cases of interest there is a standard (or "canonical") embedding, like those of the natural numbers in the integers, the integers in the rational numbers, the rational n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's Elements, Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension (mathematics), dimension, including the three-dimensional space and the ''Euclidean plane'' (dimension two). The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient History of geometry#Greek geometry, Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the Greek mathematics, ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of ''mathematical proof, proving'' all properties of the space as theorems, by starting from a few fundamental properties, called ''postulates'', which either were considered as eviden ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Product Topology
In topology and related areas of mathematics, a product space is the Cartesian product of a family of topological spaces equipped with a natural topology called the product topology. This topology differs from another, perhaps more natural-seeming, topology called the box topology, which can also be given to a product space and which agrees with the product topology when the product is over only finitely many spaces. However, the product topology is "correct" in that it makes the product space a categorical product of its factors, whereas the box topology is too fine; in that sense the product topology is the natural topology on the Cartesian product. Definition Throughout, I will be some non-empty index set and for every index i \in I, let X_i be a topological space. Denote the Cartesian product of the sets X_i by X := \prod X_ := \prod_ X_i and for every index i \in I, denote the i-th by \begin p_i :\;&& \prod_ X_j &&\;\to\; & X_i \\ .3ex && \left(x_j\r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homeomorphism
In the mathematical field of topology, a homeomorphism, topological isomorphism, or bicontinuous function is a bijective and continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are the mappings that preserve all the topological properties of a given space. Two spaces with a homeomorphism between them are called homeomorphic, and from a topological viewpoint they are the same. The word ''homeomorphism'' comes from the Greek words '' ὅμοιος'' (''homoios'') = similar or same and '' μορφή'' (''morphē'') = shape or form, introduced to mathematics by Henri Poincaré in 1895. Very roughly speaking, a topological space is a geometric object, and the homeomorphism is a continuous stretching and bending of the object into a new shape. Thus, a square and a circle are homeomorphic to each other, but a sphere and a torus are not. However, this desc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topology
In mathematics, topology (from the Greek language, Greek words , and ) is concerned with the properties of a mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformations, such as Stretch factor, stretching, Twist (mathematics), twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself. A topological space is a set (mathematics), set endowed with a structure, called a ''Topology (structure), topology'', which allows defining continuous deformation of subspaces, and, more generally, all kinds of continuity (mathematics), continuity. Euclidean spaces, and, more generally, metric spaces are examples of a topological space, as any distance or metric defines a topology. The deformations that are considered in topology are homeomorphisms and homotopy, homotopies. A property that is invariant under such deformations is a topological property. Basic exampl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bagel
A bagel ( yi, בײגל, translit=beygl; pl, bajgiel; also spelled beigel) is a bread roll originating in the Jewish communities of Poland. It is traditionally shaped by hand into a roughly hand-sized ring from yeasted wheat dough that is first boiled for a short time in water and then baked. The result is a dense, chewy, doughy interior with a browned and sometimes crisp exterior. Bagels are often topped with seeds baked on the outer crust—traditional choices include poppy and sesame seeds—or with salt grains. Different dough types include whole-grain and rye. The basic roll-with-a-hole design, hundreds of years old, allows even cooking and baking of the dough; it also allows groups of bagels to be gathered on a string or dowel for handling, transportation, and retail display. The earliest known mention of a boiled-then-baked ring-shaped bread can be found in a 13th-century Syrian cookbook, where they are referred to as . Bagels have been widely associated with Ashkenazi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Doughnut
A doughnut or donut () is a type of food made from leavened fried dough. It is popular in many countries and is prepared in various forms as a sweet snack that can be homemade or purchased in bakeries, supermarkets, food stalls, and franchised specialty vendors. ''Doughnut'' is the traditional spelling, while ''donut'' is the simplified version; the terms are used interchangeably. Doughnuts are usually deep fried from a flour dough, but other types of batters can also be used. Various toppings and flavorings are used for different types, such as sugar, chocolate or maple glazing. Doughnuts may also include water, leavening, eggs, milk, sugar, oil, shortening, and natural or artificial flavors. The two most common types are the ring doughnut and the filled doughnut, which is injected with fruit preserves (the jelly doughnut), cream, custard, or other sweet fillings. Small pieces of dough are sometimes cooked as doughnut holes. Once fried, doughnuts may be glazed with a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |





%2C_Westport%2C_CT_06880_USA_-_Feb_2013.jpg)