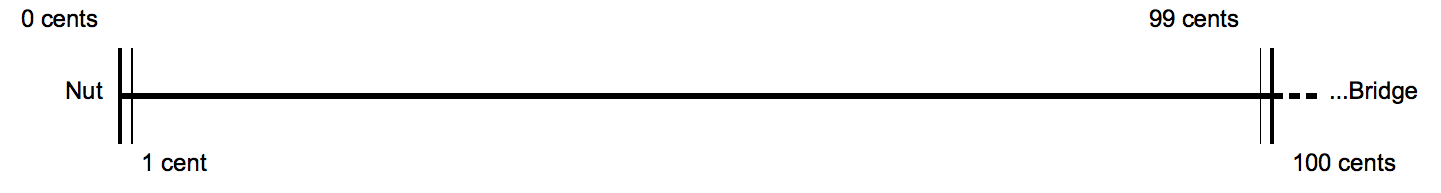|
Tetrachord Genera 1768
In music theory, a tetrachord ( el, τετράχορδoν; lat, tetrachordum) is a series of four notes separated by three interval (music), intervals. In traditional music theory, a tetrachord always spanned the interval of a perfect fourth, a 4:3 frequency proportion (approx. 498 cent (music), cents)—but in modern use it means any four-note segment of a scale (music), scale or tone row, not necessarily related to a particular tuning system. History The name comes from ''tetra'' (from Greek—"four of something") and ''chord'' (from Greek ''chordon''—"string" or "note"). In ancient Greek music theory, ''tetrachord'' signified a segment of the Musical system of ancient Greece#Systema ametabolon, an overview of the tone system, greater and lesser perfect systems bounded by ''immovable'' notes ( ); the notes between these were ''movable'' ( ). It literally means ''four strings'', originally in reference to harp-like instruments such as the lyre or the kithara, with the implicit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Music Theory
Music theory is the study of the practices and possibilities of music. ''The Oxford Companion to Music'' describes three interrelated uses of the term "music theory". The first is the " rudiments", that are needed to understand music notation (key signatures, time signatures, and rhythmic notation); the second is learning scholars' views on music from antiquity to the present; the third is a sub-topic of musicology that "seeks to define processes and general principles in music". The musicological approach to theory differs from music analysis "in that it takes as its starting-point not the individual work or performance but the fundamental materials from which it is built." Music theory is frequently concerned with describing how musicians and composers make music, including tuning systems and composition methods among other topics. Because of the ever-expanding conception of what constitutes music, a more inclusive definition could be the consideration of any sonic phenomena, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quarter Tone
A quarter tone is a pitch halfway between the usual notes of a chromatic scale or an interval about half as wide (aurally, or logarithmically) as a semitone, which itself is half a whole tone. Quarter tones divide the octave by 50 cents each, and have 24 different pitches. Quarter tone has its roots in the music of the Middle East and more specifically in Persian traditional music. However, the first evidenced proposal of quarter tones, or the quarter-tone scale (24 equal temperament), was made by 19th-century music theorists Heinrich Richter in 1823 Julian Rushton, "Quarter-Tone", ''The New Grove Dictionary of Music and Musicians'', second edition, edited by Stanley Sadie and John Tyrrell (London: Macmillan, 2001). and Mikhail Mishaqa about 1840. Composers who have written music using this scale include: Pierre Boulez, Julián Carrillo, Mildred Couper, George Enescu, Alberto Ginastera, Gérard Grisey, Alois Hába, Ljubica Marić, Charles Ives, Tristan Murail, K ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Locrian Tetrachord
Locrian may refer to: *Locrians, an ancient Greek ethnic group ** Locrian Greek, ancient Greek dialect spoken by the Locrians ** Locris, the territory of the Locrians In music: *Locrian mode, a musical mode or diatonic scale * Major Locrian scale, the scale obtained by sharpening the second and third degrees of the locrian mode * Locrian sharp 2 or Half diminished scale The half diminished scale or Sisyphean Scale is a seven-note musical scale. It is more commonly known as the Locrian 2 scale, a name that avoids confusion with the diminished scale and the half-diminished seventh chord (minor seventh, diminishe ..., a musical scale commonly used in jazz and some rock * Locrian (band), Chicago-based experimental music duo {{disambig Language and nationality disambiguation pages ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superparticular Interval
In mathematics, a superparticular ratio, also called a superparticular number or epimoric ratio, is the ratio of two consecutive integer numbers. More particularly, the ratio takes the form: :\frac = 1 + \frac where is a positive integer. Thus: Superparticular ratios were written about by Nicomachus in his treatise ''Introduction to Arithmetic''. Although these numbers have applications in modern pure mathematics, the areas of study that most frequently refer to the superparticular ratios by this name are music theory and the history of mathematics. Mathematical properties As Leonhard Euler observed, the superparticular numbers (including also the multiply superparticular ratios, numbers formed by adding an integer other than one to a unit fraction) are exactly the rational numbers whose continued fraction terminates after two terms. The numbers whose continued fraction terminates in one term are the integers, while the remaining numbers, with three or more terms in their ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Enharmonic Tetrachord Pythagorean Tuning
In modern musical notation and tuning, an enharmonic equivalent is a note, interval, or key signature that is equivalent to some other note, interval, or key signature but "spelled", or named differently. The enharmonic spelling of a written note, interval, or chord is an alternative way to write that note, interval, or chord. The term is derived from Latin ''enharmonicus'', from Late Latin ''enarmonius'', from Ancient Greek ἐναρμόνιος (''enarmónios''), from ἐν (''en'') and ἁρμονία (''harmonía''). Definition For example, in any twelve-tone equal temperament (the predominant system of musical tuning in Western music), the notes C and D are ''enharmonic'' (or ''enharmonically equivalent'') notes. Namely, they are the same key on a keyboard, and thus they are identical in pitch, although they have different names and different roles in harmony and chord progressions. Arbitrary amounts of accidentals can produce further enharmonic equivalents, such as B ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ptolemy Intense Chromatic Tetrachord
Claudius Ptolemy (; grc-gre, Πτολεμαῖος, ; la, Claudius Ptolemaeus; AD) was a mathematician, astronomer, astrologer, geographer, and music theorist, who wrote about a dozen scientific treatises, three of which were of importance to later Byzantine, Islamic, and Western European science. The first is the astronomical treatise now known as the '' Almagest'', although it was originally entitled the ''Mathēmatikē Syntaxis'' or ''Mathematical Treatise'', and later known as ''The Greatest Treatise''. The second is the ''Geography'', which is a thorough discussion on maps and the geographic knowledge of the Greco-Roman world. The third is the astrological treatise in which he attempted to adapt horoscopic astrology to the Aristotelian natural philosophy of his day. This is sometimes known as the ''Apotelesmatika'' (lit. "On the Effects") but more commonly known as the '' Tetrábiblos'', from the Koine Greek meaning "Four Books", or by its Latin equivalent ''Quadr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ptolemy Soft Chromatic Tetrachord
Claudius Ptolemy (; grc-gre, Πτολεμαῖος, ; la, Claudius Ptolemaeus; AD) was a mathematician, astronomer, astrologer, geographer, and music theorist, who wrote about a dozen scientific treatises, three of which were of importance to later Byzantine, Islamic, and Western European science. The first is the astronomical treatise now known as the '' Almagest'', although it was originally entitled the ''Mathēmatikē Syntaxis'' or ''Mathematical Treatise'', and later known as ''The Greatest Treatise''. The second is the ''Geography'', which is a thorough discussion on maps and the geographic knowledge of the Greco-Roman world. The third is the astrological treatise in which he attempted to adapt horoscopic astrology to the Aristotelian natural philosophy of his day. This is sometimes known as the ''Apotelesmatika'' (lit. "On the Effects") but more commonly known as the '' Tetrábiblos'', from the Koine Greek meaning "Four Books", or by its Latin equivalent ''Quad ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eratosthenes Chromatic Tetrachord
Eratosthenes of Cyrene (; grc-gre, Ἐρατοσθένης ; – ) was a Greek polymath: a mathematician, geographer, poet, astronomer, and music theorist. He was a man of learning, becoming the chief librarian at the Library of Alexandria. His work is comparable to what is now known as the study of geography, and he introduced some of the terminology still used today. He is best known for being the first person known to calculate the circumference of the Earth, which he did by using the extensive survey results he could access in his role at the Library; his calculation was remarkably accurate. He was also the first to calculate Earth's axial tilt, which has also proved to have remarkable accuracy. He created the first global projection of the world, incorporating parallels and meridians based on the available geographic knowledge of his era. Eratosthenes was the founder of scientific chronology; he used Egyptian and Persian records to estimate the dates of the mai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Didymos Chromatic Tetrachord
Didymos may refer to: * 65803 Didymos, a near-Earth asteroid * Didymos (music theorist), ancient Greek music theorist * Several other ancient Greeks more commonly spelt ''Didymus''; see Didymus (other) * Didymos I (1921–2014), Oriental Orthodox bishop See also * * Didimus, a genus of beetles * Didymo (''Didymosphenia geminata''), a species of diatom * * Didymus (other) {{Disambiguation, hndis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diatonic Scale
In music theory, a diatonic scale is any heptatonic scale that includes five whole steps (whole tones) and two half steps (semitones) in each octave, in which the two half steps are separated from each other by either two or three whole steps, depending on their position in the scale. This pattern ensures that, in a diatonic scale spanning more than one octave, all the half steps are maximally separated from each other (i.e. separated by at least two whole steps). The seven pitches of any diatonic scale can also be obtained by using a chain of six perfect fifths. For instance, the seven natural pitch classes that form the C-major scale can be obtained from a stack of perfect fifths starting from F: :F–C–G–D–A–E–B Any sequence of seven successive natural notes, such as C–D–E–F–G–A–B, and any transposition thereof, is a diatonic scale. Modern musical keyboards are designed so that the white notes form a diatonic scale, though transpositions of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archytas
Archytas (; el, Ἀρχύτας; 435/410–360/350 BC) was an Ancient Greek philosopher, mathematician, music theorist, astronomer, statesman, and strategist. He was a scientist of the Pythagorean school and famous for being the reputed founder of mathematical mechanics, as well as a good friend of Plato. Life and work Archytas was born in Tarentum, Magna Graecia and was the son of Mnesagoras or Hadees. For a while, he was taught by Philolaus, and was a teacher of mathematics to Eudoxus of Cnidus. Archytas and Eudoxus' student was Menaechmus. As a Pythagorean, Archytas believed that only arithmetic, not geometry, could provide a basis for satisfactory proofs. Archytas is believed to be the founder of mathematical mechanics.: ''Vitae philosophorum'' As only described in the writings of Aulus Gellius five centuries after him, he was reputed to have designed and built the first artificial, self-propelled flying device, a bird-shaped model propelled by a jet of what was probabl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cents (music)
The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each. Typically, cents are used to express small intervals, or to compare the sizes of comparable intervals in different tuning systems, and in fact the interval of one cent is too small to be perceived between successive notes. Cents, as described by Alexander John Ellis, follow a tradition of measuring intervals by logarithms that began with Juan Caramuel y Lobkowitz in the 17th century. Ellis chose to base his measures on the hundredth part of a semitone, , at Robert Holford Macdowell Bosanquet's suggestion. He made extensive measurements of musical instruments from around the world, using cents extensively to report and compare the scales employed, and further described and employed the system in his 1875 edition of Hermann von Helmholtz's ''On the Sensations of Tone''. It has become the standard method of representin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg "Click for more on -> Eratosthenes Chromatic Tetrachord")
