|
Tau Hotu Rau
Tau (uppercase Τ, lowercase τ, or \boldsymbol\tau; el, ταυ ) is the 19th letter of the Greek alphabet, representing the voiceless dental or alveolar plosive . In the system of Greek numerals, it has a value of 300. The name in English is pronounced or , but in Greek it is . This is because the pronunciation of the combination of Greek letters αυ can have the pronounciation of either , or , depending on what follows and if a diaeresis is present on the second vowel (see Greek orthography). Tau was derived from the Phoenician letter taw (𐤕). Letters that arose from tau include Roman T and Cyrillic Te (Т, т). The letter occupies the Unicode slots U+03C4 (lowercase) and U+03A4 (uppercase). In HTML, they can be produced with named entities (τ and Τ), decimal references (τ and Τ), or hexadecimal references (τ and Τ). Modern usage The lower-case letter τ is used as a symbol for: * Specific tax ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greek Alphabet
The Greek alphabet has been used to write the Greek language since the late 9th or early 8th century BCE. It is derived from the earlier Phoenician alphabet, and was the earliest known alphabetic script to have distinct letters for vowels as well as consonants. In Archaic and early Classical times, the Greek alphabet existed in many local variants, but, by the end of the 4th century BCE, the Euclidean alphabet, with 24 letters, ordered from alpha to omega, had become standard and it is this version that is still used for Greek writing today. The uppercase and lowercase forms of the 24 letters are: : , , , , , , , , , , , , , , , , , /ς, , , , , , . The Greek alphabet is the ancestor of the Latin and Cyrillic scripts. Like Latin and Cyrillic, Greek originally had only a single form of each letter; it developed the letter case distinction between uppercase and lowercase in parallel with Latin during the modern era. Sound values and conventional transcriptions for some ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
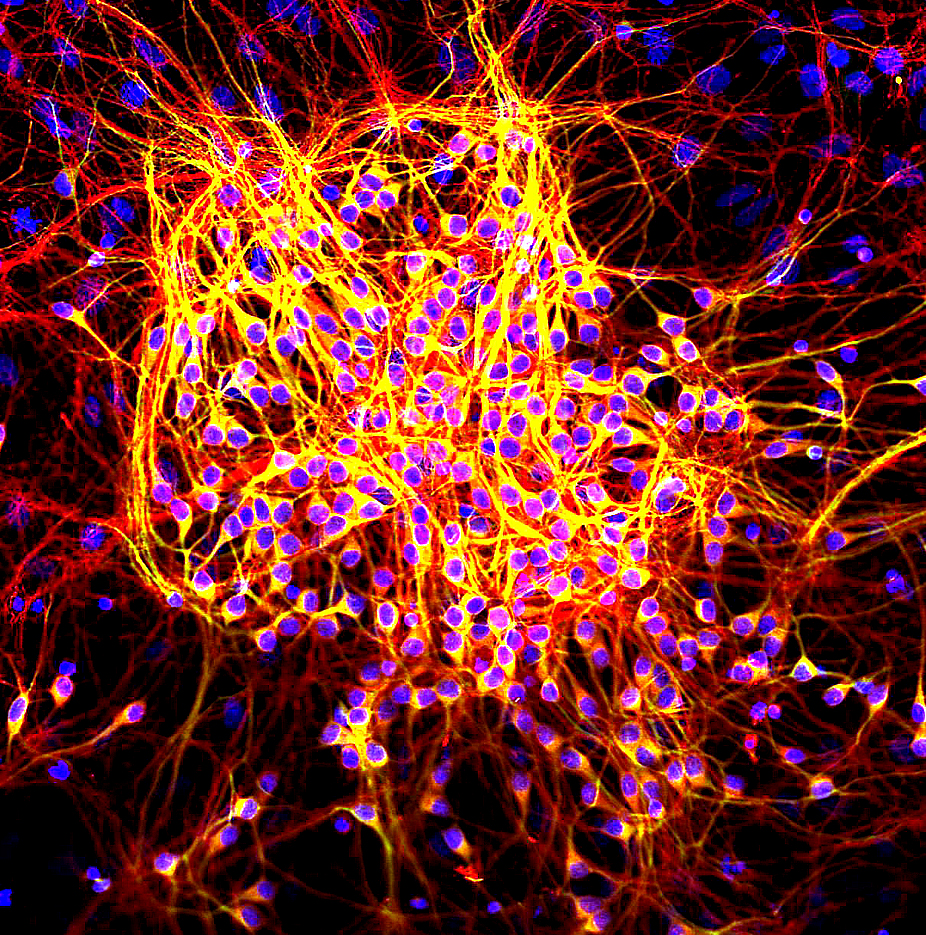
Tau (protein)
The tau proteins (abbreviated from tubulin associated unit) are a group of six highly soluble protein isoforms produced by alternative splicing from the gene ''MAPT'' (microtubule-associated protein tau). They have roles primarily in maintaining the stability of microtubules in axons and are abundant in the neurons of the central nervous system (CNS), where the cerebral cortex has the highest abundance. They are less common elsewhere but are also expressed at very low levels in CNS astrocytes and oligodendrocytes. Pathologies and dementias of the nervous system such as Alzheimer's disease and Parkinson's disease are associated with tau proteins that have become hyperphosphorylated insoluble aggregates called neurofibrillary tangles. The tau proteins were identified in 1975 as heat-stable proteins essential for microtubule assembly, and since then they have been characterized as intrinsically disordered proteins. Function Microtubule stabilization Tau proteins are found ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prouhet–Thue–Morse Constant
In mathematics, the Prouhet–Thue–Morse constant, named for Eugène Prouhet, Axel Thue, and Marston Morse, is the number—denoted by —whose binary expansion 0.01101001100101101001011001101001... is given by the Thue–Morse sequence. That is, : \tau = \sum_^ \frac = 0.412454033640 \ldots where is the element of the Prouhet–Thue–Morse sequence. Other representations The Prouhet–Thue–Morse constant can also be expressed, without using , as an infinite product, : \tau = \frac\left -\prod_^\left(1-\frac\right)\right This formula is obtained by substituting ''x'' = 1/2 into generating series for : F(x) = \sum_^ (-1)^ x^n = \prod_^ ( 1 - x^ ) The continued fraction expansion of the constant is ; 2, 2, 2, 1, 4, 3, 5, 2, 1, 4, 2, 1, 5, 44, 1, 4, 1, 2, 4, 1, … Yann Bugeaud and Martine Queffélec showed that infinitely many partial quotients of this continued fraction are 4 or 5, and infinitely many partial quotients are greater than or equal to 50. Transcende ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Translation (geometry)
In Euclidean geometry, a translation is a geometric transformation that moves every point of a figure, shape or space by the same distance in a given direction. A translation can also be interpreted as the addition of a constant vector to every point, or as shifting the origin of the coordinate system. In a Euclidean space, any translation is an isometry. As a function If \mathbf is a fixed vector, known as the ''translation vector'', and \mathbf is the initial position of some object, then the translation function T_ will work as T_(\mathbf)=\mathbf+\mathbf. If T is a translation, then the image of a subset A under the function T is the translate of A by T . The translate of A by T_ is often written A+\mathbf . Horizontal and vertical translations In geometry, a vertical translation (also known as vertical shift) is a translation of a geometric object in a direction parallel to the vertical axis of the Cartesian coordinate system. Often, vertical translatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
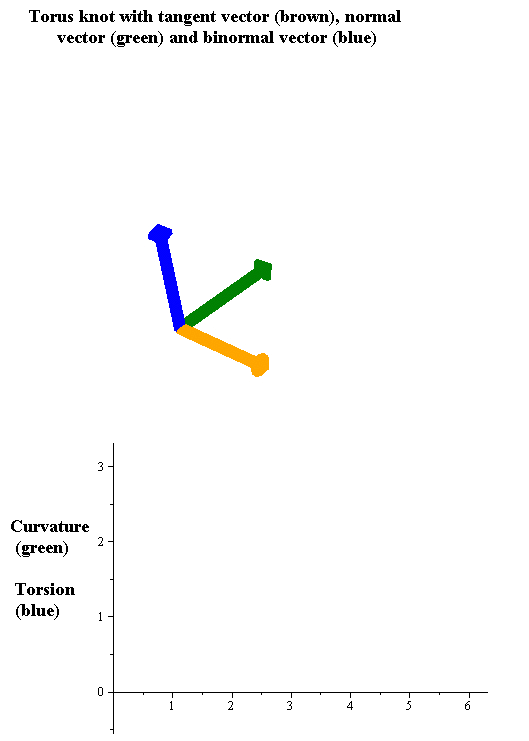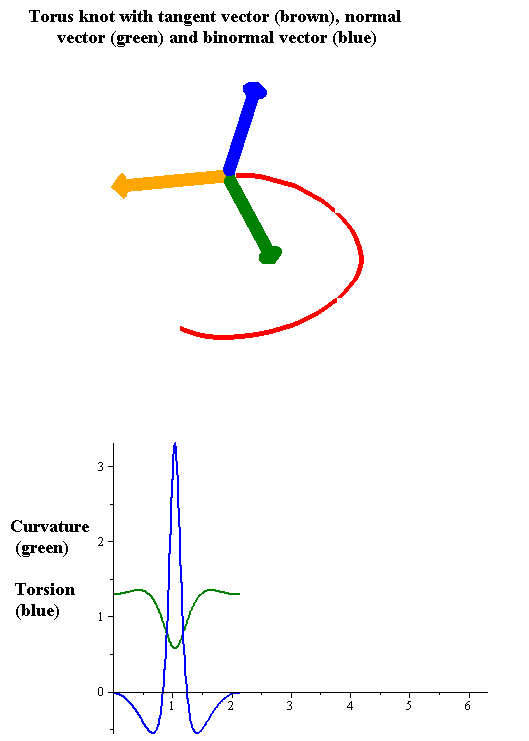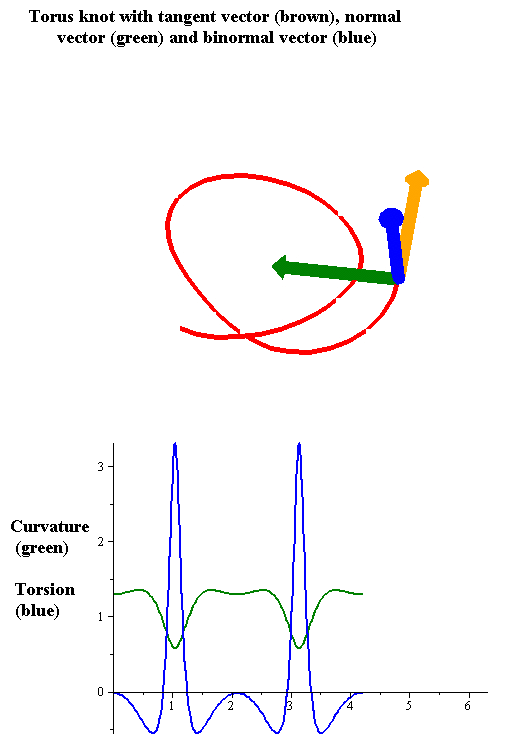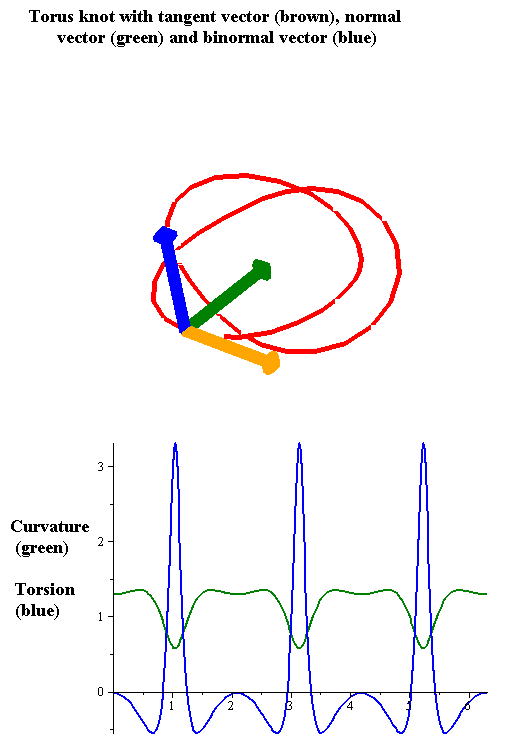
Torsion Of A Curve
In the differential geometry of curves in three dimensions, the torsion of a curve measures how sharply it is twisting out of the osculating plane. Taken together, the curvature and the torsion of a space curve are analogous to the curvature of a plane curve. For example, they are coefficients in the system of differential equations for the Frenet frame given by the Frenet–Serret formulas. Definition Let be a space curve parametrized by arc length and with the unit tangent vector . If the curvature of at a certain point is not zero then the principal normal vector and the binormal vector at that point are the unit vectors : \mathbf=\frac, \quad \mathbf=\mathbf\times\mathbf respectively, where the prime denotes the derivative of the vector with respect to the parameter . The torsion measures the speed of rotation of the binormal vector at the given point. It is found from the equation : \mathbf' = -\tau\mathbf. which means : \tau = -\mathbf\cdot\mathb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tau Function (other) , an arithmetic function giving the number of divisors of an integer
{{disambiguation ...
Tau function may refer to: * Tau function (integrable systems), in integrable systems * Ramanujan tau function, giving the Fourier coefficients of the Ramanujan modular form * Divisor function In mathematics, and specifically in number theory, a divisor function is an arithmetic function related to the divisors of an integer. When referred to as ''the'' divisor function, it counts the ''number of divisors of an integer'' (includi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tau (mathematical Constant)
A turn is a unit of plane angle measurement equal to radians, 360 degrees or 400 gradians. Subdivisions of a turn include half-turns, quarter-turns, centiturns, milliturns, etc. The closely related terms ''cycle'' and ''revolution'' are not equivalent to a turn. Subdivisions A turn can be divided in 100 centiturns or milliturns, with each milliturn corresponding to an angle of 0.36°, which can also be written as 21′ 36″. A protractor divided in centiturns is normally called a "percentage protractor". Binary fractions of a turn are also used. Sailors have traditionally divided a turn into 32 compass points, which implicitly have an angular separation of 1/32 turn. The ''binary degree'', also known as the ''binary radian'' (or ''brad''), is turn. The binary degree is used in computing so that an angle can be represented to the maximum possible precision in a single byte. Other measures of angle used in computing may be based on divid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stopping Time
In probability theory, in particular in the study of stochastic processes, a stopping time (also Markov time, Markov moment, optional stopping time or optional time ) is a specific type of “random time”: a random variable whose value is interpreted as the time at which a given stochastic process exhibits a certain behavior of interest. A stopping time is often defined by a stopping rule, a mechanism for deciding whether to continue or stop a process on the basis of the present position and past events, and which will almost always lead to a decision to stop at some finite time. Stopping times occur in decision theory, and the optional stopping theorem is an important result in this context. Stopping times are also frequently applied in mathematical proofs to “tame the continuum of time”, as Chung put it in his book (1982). Definition Discrete time Let \tau be a random variable, which is defined on the filtered probability space (\Omega, \mathcal F, (\mathcal F_n)_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kendall Tau Rank Correlation Coefficient
In statistics, the Kendall rank correlation coefficient, commonly referred to as Kendall's τ coefficient (after the Greek letter τ, tau), is a statistic used to measure the ordinal association between two measured quantities. A τ test is a non-parametric hypothesis test for statistical dependence based on the τ coefficient. It is a measure of rank correlation: the similarity of the orderings of the data when ranked by each of the quantities. It is named after Maurice Kendall, who developed it in 1938, though Gustav Fechner had proposed a similar measure in the context of time series in 1897. Intuitively, the Kendall correlation between two variables will be high when observations have a similar (or identical for a correlation of 1) rank (i.e. relative position label of the observations within the variable: 1st, 2nd, 3rd, etc.) between the two variables, and low when observations have a dissimilar (or fully different for a correlation of −1) rank between the two vari ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Golden Ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities a and b with a > b > 0, where the Greek letter phi ( or \phi) denotes the golden ratio. The constant \varphi satisfies the quadratic equation \varphi^2 = \varphi + 1 and is an irrational number with a value of The golden ratio was called the extreme and mean ratio by Euclid, and the divine proportion by Luca Pacioli, and also goes by several other names. Mathematicians have studied the golden ratio's properties since antiquity. It is the ratio of a regular pentagon's diagonal to its side and thus appears in the construction of the dodecahedron and icosahedron. A golden rectangle—that is, a rectangle with an aspect ratio of \varphi—may be cut into a square and a smaller rectangle with the same aspect ratio. The golden ratio has been used to analyze the proportions of natural o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divisor Function
In mathematics, and specifically in number theory, a divisor function is an arithmetic function related to the divisors of an integer. When referred to as ''the'' divisor function, it counts the ''number of divisors of an integer'' (including 1 and the number itself). It appears in a number of remarkable identities, including relationships on the Riemann zeta function and the Eisenstein series of modular forms. Divisor functions were studied by Ramanujan, who gave a number of important congruences and identities; these are treated separately in the article Ramanujan's sum. A related function is the divisor summatory function, which, as the name implies, is a sum over the divisor function. Definition The sum of positive divisors function σ''z''(''n''), for a real or complex number ''z'', is defined as the sum of the ''z''th powers of the positive divisors of ''n''. It can be expressed in sigma notation as :\sigma_z(n)=\sum_ d^z\,\! , where is shorthand for "''d'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chronic Traumatic Encephalopathy
Chronic traumatic encephalopathy (CTE) is a neurodegenerative disease linked to repeated trauma to the head. The encephalopathy symptoms can include behavioral problems, mood problems, and problems with thinking. The disease often gets worse over time and can result in dementia. It is unclear if the risk of suicide is altered. Most documented cases have occurred in athletes involved in striking-based combat sports, such as boxing, kickboxing, mixed martial arts, and Muay Thai—hence its original name ''dementia pugilistica'' (Latin for "fistfighter's dementia")—and contact sports such as American football, Australian rules football, professional wrestling, ice hockey, rugby, and association football (soccer), in semi-contact sports such as baseball and basketball, and military combat arms occupations. Other risk factors include being in the military, prior domestic violence, and repeated banging of the head. The exact amount of trauma required for the condition to occur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |