|
Tachyonic Field
In physics, a tachyonic field, or simply tachyon, is a quantum field with an imaginary mass. Although tachyonic particles (particles that move faster than light) are a purely hypothetical concept that violate a number of essential physical principles, at least one field with imaginary mass, the Higgs field, is believed to exist. Under no circumstances do any excitations of tachyonic fields ever propagate faster than light—the presence or absence of a tachyonic (imaginary) mass has no effect on the maximum velocity of signals, and so unlike faster-than-light particles there is no violation of causality. Tachyonic fields play an important role in physics and are discussed in popular books. The term "tachyon" was coined by Gerald Feinberg in a 1967 paper that studied quantum fields with imaginary mass. Feinberg believed such fields permitted faster than light propagation, but it was soon realized that this was not the case. Instead, the imaginary mass creates an instability ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Field
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines classical field theory, special relativity, and quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles and in condensed matter physics to construct models of quasiparticles. QFT treats particles as excited states (also called Quantum, quanta) of their underlying quantum field (physics), fields, which are more fundamental than the particles. The equation of motion of the particle is determined by minimization of the Lagrangian, a functional of fields associated with the particle. Interactions between particles are described by interaction terms in the Lagrangian (field theory), Lagrangian involving their corresponding quantum fields. Each interaction can be visually represented by Feynman diagrams according to perturbation theory (quantum mechanics), perturbation theory in quantum mechanics. History Quantum field theory emerged from the wo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Field Theory
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines classical field theory, special relativity, and quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles and in condensed matter physics to construct models of quasiparticles. QFT treats particles as excited states (also called Quantum, quanta) of their underlying quantum field (physics), fields, which are more fundamental than the particles. The equation of motion of the particle is determined by minimization of the Lagrangian, a functional of fields associated with the particle. Interactions between particles are described by interaction terms in the Lagrangian (field theory), Lagrangian involving their corresponding quantum fields. Each interaction can be visually represented by Feynman diagrams according to perturbation theory (quantum mechanics), perturbation theory in quantum mechanics. History Quantum field theory emerged from the wo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
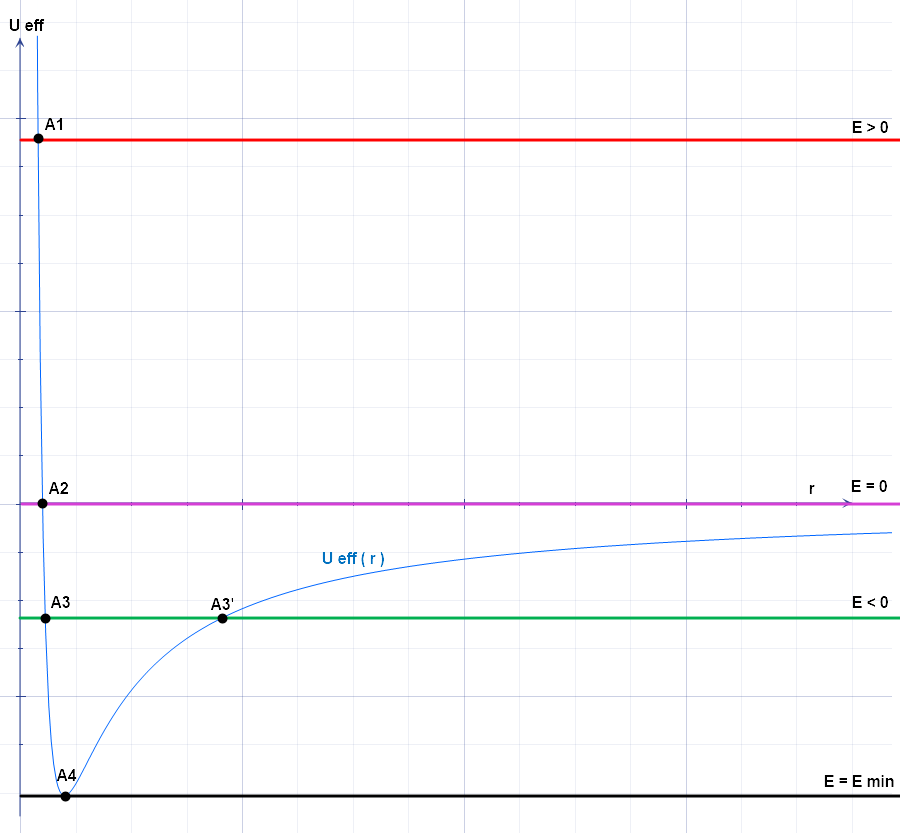
Effective Potential
The effective potential (also known as effective potential energy) combines multiple, perhaps opposing, effects into a single potential. In its basic form, it is the sum of the 'opposing' centrifugal potential energy with the potential energy of a dynamical system. It may be used to determine the orbits of planets (both Newtonian and relativistic) and to perform semi-classical atomic calculations, and often allows problems to be reduced to fewer dimensions. Definition The basic form of potential U_\text is defined as: U_\text(\mathbf) = \frac + U(\mathbf), where *''L'' is the angular momentum *''r'' is the distance between the two masses *''μ'' is the reduced mass of the two bodies (approximately equal to the mass of the orbiting body if one mass is much larger than the other); and *''U''(''r'') is the general form of the potential. The effective force, then, is the negative gradient of the effective potential: \begin \mathbf_\text &= -\nabla U_\text(\mathbf) \\ &= \frac \h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Model Of Particle Physics
The Standard Model of particle physics is the theory describing three of the four known fundamental forces (electromagnetic, weak and strong interactions - excluding gravity) in the universe and classifying all known elementary particles. It was developed in stages throughout the latter half of the 20th century, through the work of many scientists worldwide, with the current formulation being finalized in the mid-1970s upon experimental confirmation of the existence of quarks. Since then, proof of the top quark (1995), the tau neutrino (2000), and the Higgs boson (2012) have added further credence to the Standard Model. In addition, the Standard Model has predicted various properties of weak neutral currents and the W and Z bosons with great accuracy. Although the Standard Model is believed to be theoretically self-consistent and has demonstrated huge successes in providing experimental predictions, it leaves some phenomena unexplained. It falls short of being a complete the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scalar Field Theory
In theoretical physics, scalar field theory can refer to a relativistically invariant classical or quantum theory of scalar fields. A scalar field is invariant under any Lorentz transformation. The only fundamental scalar quantum field that has been observed in nature is the Higgs field. However, scalar quantum fields feature in the effective field theory descriptions of many physical phenomena. An example is the pion, which is actually a pseudoscalar. Since they do not involve polarization complications, scalar fields are often the easiest to appreciate second quantization through. For this reason, scalar field theories are often used for purposes of introduction of novel concepts and techniques. The signature of the metric employed below is . Classical scalar field theory A general reference for this section is Ramond, Pierre (2001-12-21). Field Theory: A Modern Primer (Second Edition). USA: Westview Press. , Ch 1. Linear (free) theory The most basic scalar field theo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bosonic String Theory
Bosonic string theory is the original version of string theory, developed in the late 1960s and named after Satyendra Nath Bose. It is so called because it contains only bosons in the spectrum. In the 1980s, supersymmetry was discovered in the context of string theory, and a new version of string theory called superstring theory (supersymmetric string theory) became the real focus. Nevertheless, bosonic string theory remains a very useful model to understand many general features of perturbative string theory, and many theoretical difficulties of superstrings can actually already be found in the context of bosonic strings. Problems Although bosonic string theory has many attractive features, it falls short as a viable physical model in two significant areas. First, it predicts only the existence of bosons whereas many physical particles are fermions. Second, it predicts the existence of a mode of the string with imaginary mass, implying that the theory has an instability t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inflation (cosmology)
In physical cosmology, cosmic inflation, cosmological inflation, or just inflation, is a theory of exponential expansion of space in the early universe. The inflationary epoch lasted from seconds after the conjectured Big Bang singularity to some time between and seconds after the singularity. Following the inflationary period, the universe continued to expand, but at a slower rate. The acceleration of this expansion due to dark energy began after the universe was already over 7.7 billion years old (5.4 billion years ago). Inflation theory was developed in the late 1970s and early 80s, with notable contributions by several theoretical physicists, including Alexei Starobinsky at Landau Institute for Theoretical Physics, Alan Guth at Cornell University, and Andrei Linde at Lebedev Physical Institute. Alexei Starobinsky, Alan Guth, and Andrei Linde won the 2014 Kavli Prize "for pioneering the theory of cosmic inflation." It was developed further in the ear ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inflaton
The inflaton field is a hypothetical scalar field which is conjectured to have driven cosmic inflation in the very early universe. The field, originally postulated by Alan Guth, provides a mechanism by which a period of rapid expansion from 10−35 to 10−34 seconds after the initial expansion can be generated, forming a universe consistent with observed spatial isotropy and homogeneity. Cosmological inflation The basic model of inflation proceeds in three phases: * Expanding vacuum state with high potential energy * Phase transition to true vacuum * Slow roll and reheating Expanding vacuum state with high potential energy In quantum field theory, a vacuum state or vacuum is a state of quantum fields which is at locally minimal potential energy. Quantum particles are excitations which deviate from this minimal potential energy state, therefore a vacuum state has no particles in it. Depending on the specifics of a quantum field theory, it can have more than on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
BCS Theory
BCS theory or Bardeen–Cooper–Schrieffer theory (named after John Bardeen, Leon Cooper, and John Robert Schrieffer) is the first microscopic theory of superconductivity since Heike Kamerlingh Onnes's 1911 discovery. The theory describes superconductivity as a microscopic effect caused by a condensation of Cooper pairs. The theory is also used in nuclear physics to describe the pairing interaction between nucleons in an atomic nucleus. It was proposed by Bardeen, Cooper, and Schrieffer in 1957; they received the Nobel Prize in Physics for this theory in 1972. History Rapid progress in the understanding of superconductivity gained momentum in the mid-1950s. It began with the 1948 paper, "On the Problem of the Molecular Theory of Superconductivity", where Fritz London proposed that the phenomenological London equations may be consequences of the coherence of a quantum state. In 1953, Brian Pippard, motivated by penetration experiments, proposed that this would modify the Lo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ginzburg–Landau Theory
In physics, Ginzburg–Landau theory, often called Landau–Ginzburg theory, named after Vitaly Ginzburg and Lev Landau, is a mathematical physical theory used to describe superconductivity. In its initial form, it was postulated as a phenomenological model which could describe type-I superconductors without examining their microscopic properties. One GL-type superconductor is the famous YBCO, and generally all Cuprates. Later, a version of Ginzburg–Landau theory was derived from the Bardeen–Cooper–Schrieffer microscopic theory by Lev Gor'kov, thus showing that it also appears in some limit of microscopic theory and giving microscopic interpretation of all its parameters. The theory can also be given a general geometric setting, placing it in the context of Riemannian geometry, where in many cases exact solutions can be given. This general setting then extends to quantum field theory and string theory, again owing to its solvability, and its close relation to other, simi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spontaneous Symmetry Breaking
Spontaneous symmetry breaking is a spontaneous process of symmetry breaking, by which a physical system in a symmetric state spontaneously ends up in an asymmetric state. In particular, it can describe systems where the equations of motion or the Lagrangian obey symmetries, but the lowest-energy vacuum solutions do not exhibit that same symmetry. When the system goes to one of those vacuum solutions, the symmetry is broken for perturbations around that vacuum even though the entire Lagrangian retains that symmetry. Overview By definition, spontaneous symmetry breaking requires the existence of physical laws (e.g. quantum mechanics) which are invariant under a symmetry transformation (such as translation or rotation), so that any pair of outcomes differing only by that transformation have the same probability distribution. For example if measurements of an observable at any two different positions have the same probability distribution, the observable has translational symmetry. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Local Maximum
In mathematical analysis, the maxima and minima (the respective plurals of maximum and minimum) of a function, known collectively as extrema (the plural of extremum), are the largest and smallest value of the function, either within a given range (the ''local'' or ''relative'' extrema), or on the entire domain (the ''global'' or ''absolute'' extrema). Pierre de Fermat was one of the first mathematicians to propose a general technique, adequality, for finding the maxima and minima of functions. As defined in set theory, the maximum and minimum of a set are the greatest and least elements in the set, respectively. Unbounded infinite sets, such as the set of real numbers, have no minimum or maximum. Definition A real-valued function ''f'' defined on a domain ''X'' has a global (or absolute) maximum point at ''x''∗, if for all ''x'' in ''X''. Similarly, the function has a global (or absolute) minimum point at ''x''∗, if for all ''x'' in ''X''. The value of the function at a m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |



.png)