|
Truncated Normal Distribution
In probability and statistics, the truncated normal distribution is the probability distribution derived from that of a normally distributed random variable by bounding the random variable from either below or above (or both). The truncated normal distribution has wide applications in statistics and econometrics. Definitions Suppose X has a normal distribution with mean \mu and variance \sigma^2 and lies within the interval (a,b), \text \; -\infty \leq a < b \leq \infty . Then conditional on has a truncated normal distribution. Its , , for , is given by : and by otherwise. Here, : is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Instituto Superior Técnico
Instituto Superior Técnico MHSE • MHIP (IST, also known colloquially as Técnico, and stylized TÉCNICO LISBOA) is a public school of engineering and technology, part of University of Lisbon. It was founded as an autonomous school in 1911, and integrated in the Universidade Técnica de Lisboa in 1930. IST is the largest school of engineering in Portugal by number of enrolled students, faculty size, scientific production and patents. IST has three ''campi'', all located in the Lisbon metropolitan area: Alameda in Lisbon, Taguspark in Oeiras and Tecnológico e Nuclear Campus in Loures, and consists of ten departments that are responsible for teaching the undergraduate and postgraduate programs. Each department is organized in sections, which group together specific subjects within its scientific area. In addition, the laboratories of the several departments support the teaching and research activities carried out at IST. It offers 18 undergraduate programmes attended ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Catastrophic Cancellation
In numerical analysis, catastrophic cancellation is the phenomenon that subtracting good approximations to two nearby numbers may yield a very bad approximation to the difference of the original numbers. For example, if there are two studs, one L_1 = 254.5\,\text long and the other L_2 = 253.5\,\text long, and they are measured with a ruler that is good only to the centimeter, then the approximations could come out to be \tilde L_1 = 255\,\text and \tilde L_2 = 253\,\text. These may be good approximations, in relative error, to the true lengths: the approximations are in error by less than 2% of the true lengths, , L_1 - \tilde L_1, /, L_1, < 2\%. However, if the ''approximate'' lengths are subtracted, the difference will be , even though the true difference between the lengths is . The difference of the approximations, |
PERT Distribution
In probability and statistics, the PERT distribution is a family of continuous probability distributions defined by the minimum (a), most likely (b) and maximum (c) values that a variable can take. It is a transformation of the four-parameter beta distribution with an additional assumption that its expected value is : \mu = \frac 6. The mean of the distribution is therefore defined as the weighted average of the minimum, most likely and maximum values that the variable may take, with four times the weight applied to the most likely value. This assumption about the mean was first proposed in Clark, 1962 for estimating the effect of uncertainty of task durations on the outcome of a project schedule being evaluated using the program evaluation and review technique, hence its name. The mathematics of the distribution resulted from the authors' desire to make the standard deviation equal to about 1/6 of the range. The PERT distribution is widely used in risk analysis to represent the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectified Gaussian Distribution
In probability theory, the rectified Gaussian distribution is a modification of the Gaussian distribution when its negative elements are reset to 0 (analogous to an electronic rectifier). It is essentially a mixture of a discrete distribution (constant 0) and a continuous distribution (a truncated Gaussian distribution with interval (0,\infty)) as a result of censoring. Density function The probability density function of a rectified Gaussian distribution, for which random variables ''X'' having this distribution, derived from the normal distribution \mathcal(\mu,\sigma^2), are displayed as X \sim \mathcal^(\mu,\sigma^2) , is given by f(x;\mu,\sigma^2) =\Phi\delta(x)+ \frac\; e^\textrm(x). Here, \Phi(x) is the cumulative distribution function (cdf) of the standard normal distribution: \Phi(x) = \frac \int_^x e^ \, dt \quad x\in\mathbb, \delta(x) is the Dirac delta function \delta(x) = \begin +\infty, & x = 0 \\ 0, & x \ne 0 \end and, \textrm(x) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modified Half-normal Distribution
In probability theory and statistics, the half-normal distribution is a special case of the folded normal distribution. Let X follow an ordinary normal distribution, N(0,\sigma^2). Then, Y=, X, follows a half-normal distribution. Thus, the half-normal distribution is a fold at the mean of an ordinary normal distribution with mean zero. Properties Using the \sigma parametrization of the normal distribution, the probability density function (PDF) of the half-normal is given by : f_Y(y; \sigma) = \frac\exp \left( -\frac \right) \quad y \geq 0, where E = \mu = \frac. Alternatively using a scaled precision (inverse of the variance) parametrization (to avoid issues if \sigma is near zero), obtained by setting \theta=\frac, the probability density function is given by : f_Y(y; \theta) = \frac\exp \left( -\frac \right) \quad y \geq 0, where E = \mu = \frac. The cumulative distribution function (CDF) is given by : F_Y(y; \sigma) = \int_0^y \frac\sqrt \, \exp \left( -\frac \rig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Folded Normal Distribution
The folded normal distribution is a probability distribution related to the normal distribution. Given a normally distributed random variable ''X'' with mean ''μ'' and variance ''σ''2, the random variable ''Y'' = , ''X'', has a folded normal distribution. Such a case may be encountered if only the magnitude of some variable is recorded, but not its sign. The distribution is called "folded" because probability mass to the left of ''x'' = 0 is folded over by taking the absolute value. In the physics of heat conduction, the folded normal distribution is a fundamental solution of the heat equation on the half space; it corresponds to having a perfect insulator on a hyperplane through the origin. Definitions Density The probability density function (PDF) is given by :f_Y(x;\mu,\sigma^2)= \frac \, e^ + \frac \, e^ for ''x'' ≥ 0, and 0 everywhere else. An alternative formulation is given by : f\left(x \right)=\sqrte^\cosh, where cosh is the cosine Hyperbolic function. It f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
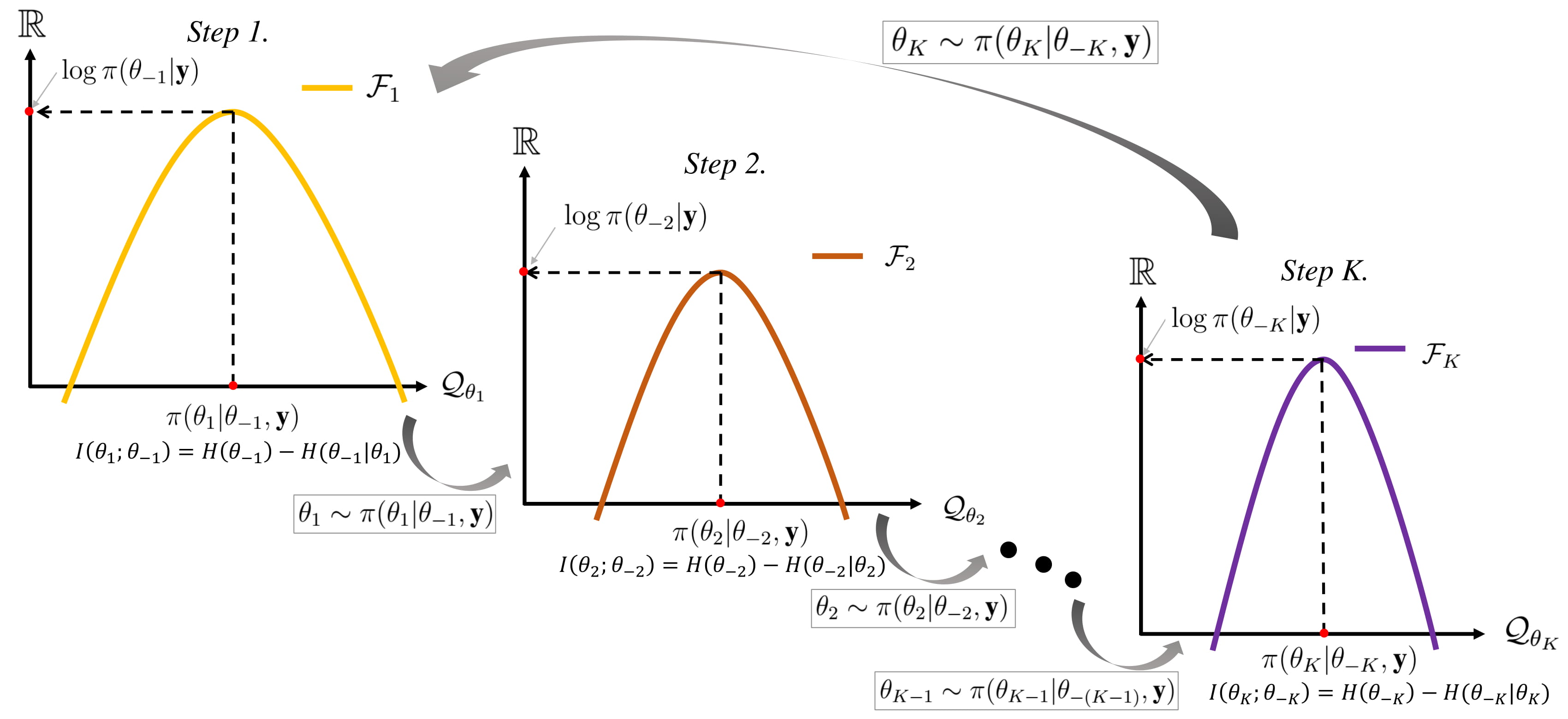
Gibbs Sampling
In statistics, Gibbs sampling or a Gibbs sampler is a Markov chain Monte Carlo (MCMC) algorithm for obtaining a sequence of observations which are approximated from a specified multivariate probability distribution, when direct sampling is difficult. This sequence can be used to approximate the joint distribution (e.g., to generate a histogram of the distribution); to approximate the marginal distribution of one of the variables, or some subset of the variables (for example, the unknown parameters or latent variables); or to compute an integral (such as the expected value of one of the variables). Typically, some of the variables correspond to observations whose values are known, and hence do not need to be sampled. Gibbs sampling is commonly used as a means of statistical inference, especially Bayesian inference. It is a randomized algorithm (i.e. an algorithm that makes use of random numbers), and is an alternative to deterministic algorithms for statistical inference su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ziggurat Algorithm
The ziggurat algorithm is an algorithm for pseudo-random number sampling. Belonging to the class of rejection sampling algorithms, it relies on an underlying source of uniformly-distributed random numbers, typically from a pseudo-random number generator, as well as precomputed tables. The algorithm is used to generate values from a monotonically decreasing probability distribution. It can also be applied to symmetric unimodal distributions, such as the normal distribution, by choosing a value from one half of the distribution and then randomly choosing which half the value is considered to have been drawn from. It was developed by George Marsaglia and others in the 1960s. A typical value produced by the algorithm only requires the generation of one random floating-point value and one random table index, followed by one table lookup, one multiply operation and one comparison. Sometimes (2.5% of the time, in the case of a normal or exponential distribution when using typical ta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
R (programming Language)
R is a programming language for statistical computing and graphics supported by the R Core Team and the R Foundation for Statistical Computing. Created by statisticians Ross Ihaka and Robert Gentleman, R is used among data miners, bioinformaticians and statisticians for data analysis and developing statistical software. Users have created packages to augment the functions of the R language. According to user surveys and studies of scholarly literature databases, R is one of the most commonly used programming languages used in data mining. R ranks 12th in the TIOBE index, a measure of programming language popularity, in which the language peaked in 8th place in August 2020. The official R software environment is an open-source free software environment within the GNU package, available under the GNU General Public License. It is written primarily in C, Fortran, and R itself (partially self-hosting). Precompiled executables are provided for various operating systems. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Transform Method
Inverse transform sampling (also known as inversion sampling, the inverse probability integral transform, the inverse transformation method, Smirnov transform, or the golden ruleAalto University, N. Hyvönen, Computational methods in inverse problems. Twelfth lecture https://noppa.tkk.fi/noppa/kurssi/mat-1.3626/luennot/Mat-1_3626_lecture12.pdf) is a basic method for pseudo-random number sampling, i.e., for generating sample numbers at random from any probability distribution given its cumulative distribution function. Inverse transformation sampling takes uniform samples of a number u between 0 and 1, interpreted as a probability, and then returns the largest number x from the domain of the distribution P(X) such that P(-\infty , e.g. from U \sim \mathrm ,1 #Find the inverse of the desired CDF, e.g. F_X^(x). # Compute X=F_X^(u). The computed random variable X has distribution F_X(x). Expressed differently, given a continuous uniform variable U in ,1/math> and an invertible cum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |