|
Trinomial Triangle
The trinomial triangle is a variation of Pascal's triangle. The difference between the two is that an entry in the trinomial triangle is the sum of the ''three'' (rather than the ''two'' in Pascal's triangle) entries above it: \begin & & & & 1\\ & & & 1& 1&1\\ & & 1& 2& 3&2&1\\ &1& 3& 6& 7&6&3&1\\ 1&4&10&16&19&16&10&4&1\end The k-th entry of the n-th row is denoted by : _2. Rows are counted starting from 0. The entries of the n-th row are indexed starting with -n from the left, and the middle entry has index 0. The symmetry of the entries of a row about the middle entry is expressed by the relationship : _2=_2 Properties The n-th row corresponds to the coefficients in the polynomial expansion of the expansion of the trinomial (1 + x + x^2) raised to the n-th power: :\left(1+x+x^2\right)^n= \sum _^_2 x^=\sum _^_2 x^ or, symmetrically, :\left(1+x+1/x\right)^n=\sum_^_2 x^k, hence the alternative name trinomial coefficients because of their relationship to the multinom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pascal's Triangle
In mathematics, Pascal's triangle is an infinite triangular array of the binomial coefficients which play a crucial role in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although other mathematicians studied it centuries before him in Persia, India, China, Germany, and Italy. The rows of Pascal's triangle are conventionally enumerated starting with row n = 0 at the top (the 0th row). The entries in each row are numbered from the left beginning with k = 0 and are usually staggered relative to the numbers in the adjacent rows. The triangle may be constructed in the following manner: In row 0 (the topmost row), there is a unique nonzero entry 1. Each entry of each subsequent row is constructed by adding the number above and to the left with the number above and to the right, treating blank entries as 0. For example, the initial number of row 1 (or any other row) is 1 (the sum of 0 and 1), whereas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
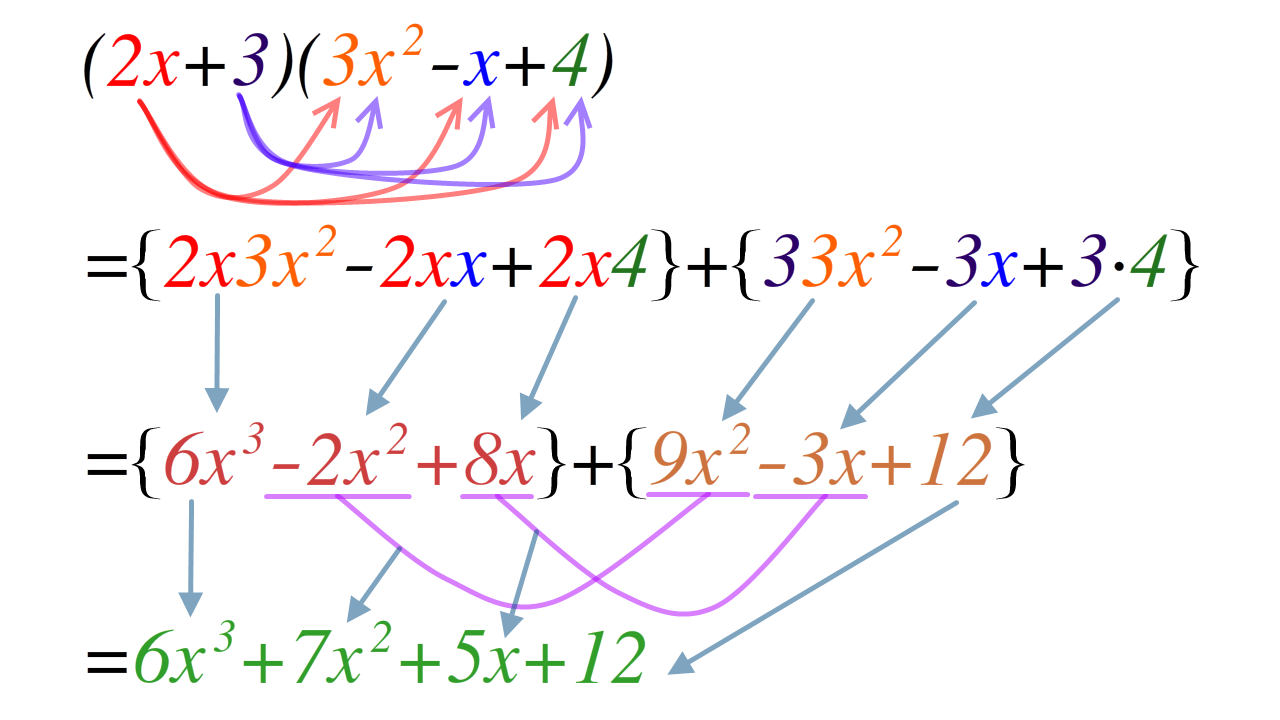
Polynomial Expansion
In mathematics, an expansion of a product of sums expresses it as a sum of products by using the fact that multiplication distributes over addition. Expansion of a polynomial expression can be obtained by repeatedly replacing subexpressions that multiply two other subexpressions, at least one of which is an addition, by the equivalent sum of products, continuing until the expression becomes a sum of (repeated) products. During the expansion, simplifications such as grouping of like terms or cancellations of terms may also be applied. Instead of multiplications, the expansion steps could also involve replacing powers of a sum of terms by the equivalent expression obtained from the binomial formula; this is a shortened form of what would happen if the power were treated as a repeated multiplication, and expanded repeatedly. It is customary to reintroduce powers in the final result when terms involve products of identical symbols. Simple examples of polynomial expansions are the wel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trinomial
In elementary algebra, a trinomial is a polynomial consisting of three terms or monomials. Examples of trinomial expressions # 3x + 5y + 8z with x, y, z variables # 3t + 9s^2 + 3y^3 with t, s, y variables # 3ts + 9t + 5s with t, s variables # ax^2+bx+c, the quadratic polynomial in standard form with a,b,c variables.Quadratic expressions are not always trinomials, the expressions' appearance can vary. # A x^a y^b z^c + B t + C s with x, y, z, t, s variables, a, b, c nonnegative integers and A, B, C any constants. # Px^a + Qx^b + Rx^c where x is variable and constants a, b, c are nonnegative integers and P, Q, R any constants. Trinomial equation A trinomial equation is a polynomial equation involving three terms. An example is the equation x = q + x^m studied by Johann Heinrich Lambert in the 18th century. Some notable trinomials * The quadratic trinomial in standard form (as from above): :: ax^2+bx+c * sum or difference of two cubes: :: a^3 \pm b^3 = (a \pm b)(a^2 \mp ab + b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multinomial Coefficients
In mathematics, the multinomial theorem describes how to expand a power of a sum in terms of powers of the terms in that sum. It is the generalization of the binomial theorem from binomials to multinomials. Theorem For any positive integer and any non-negative integer , the multinomial theorem describes how a sum with terms expands when raised to the th power: (x_1 + x_2 + \cdots + x_m)^n = \sum_ x_1^ \cdot x_2^ \cdots x_m^ where = \frac is a multinomial coefficient. The sum is taken over all combinations of nonnegative integer indices through such that the sum of all is . That is, for each term in the expansion, the exponents of the must add up to . In the case , this statement reduces to that of the binomial theorem. Example The third power of the trinomial is given by (a+b+c)^3 = a^3 + b^3 + c^3 + 3 a^2 b + 3 a^2 c + 3 b^2 a + 3 b^2 c + 3 c^2 a + 3 c^2 b + 6 a b c. This can be computed by hand using the distributive property of multiplication over addition ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Numbers
A triangular number or triangle number counts objects arranged in an equilateral triangle. Triangular numbers are a type of figurate number, other examples being square numbers and cube numbers. The th triangular number is the number of dots in the triangular arrangement with dots on each side, and is equal to the sum of the natural numbers from 1 to . The first 100 terms sequence of triangular numbers, starting with the 0th triangular number, are Formula The triangular numbers are given by the following explicit formulas: where \textstyle is notation for a binomial coefficient. It represents the number of distinct pairs that can be selected from objects, and it is read aloud as " plus one choose two". The fact that the nth triangular number equals n(n+1)/2 can be illustrated using a visual proof. For every triangular number T_n, imagine a "half-rectangle" arrangement of objects corresponding to the triangular number, as in the figure below. Copying this arrangement ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recurrence Formula
In mathematics, a recurrence relation is an equation according to which the nth term of a sequence of numbers is equal to some combination of the previous terms. Often, only k previous terms of the sequence appear in the equation, for a parameter k that is independent of n; this number k is called the ''order'' of the relation. If the values of the first k numbers in the sequence have been given, the rest of the sequence can be calculated by repeatedly applying the equation. In ''linear recurrences'', the th term is equated to a linear function of the k previous terms. A famous example is the recurrence for the Fibonacci numbers, F_n=F_+F_ where the order k is two and the linear function merely adds the two previous terms. This example is a linear recurrence with constant coefficients, because the coefficients of the linear function (1 and 1) are constants that do not depend on n. For these recurrences, one can express the general term of the sequence as a closed-form expression of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leonhard Euler
Leonhard Euler ( ; ; ; 15 April 170718 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential discoveries in many other branches of mathematics, such as analytic number theory, complex analysis, and infinitesimal calculus. He also introduced much of modern mathematical terminology and Mathematical notation, notation, including the notion of a mathematical function. He is known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory. Euler has been called a "universal genius" who "was fully equipped with almost unlimited powers of imagination, intellectual gifts and extraordinary memory". He spent most of his adult life in Saint Petersburg, Russia, and in Berlin, then the capital of Kingdom of Prussia, Prussia. Euler is credited for popularizing the Greek letter \pi (lowercase Pi (letter), pi) to denote Pi, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generating Function
In mathematics, a generating function is a representation of an infinite sequence of numbers as the coefficients of a formal power series. Generating functions are often expressed in closed form (rather than as a series), by some expression involving operations on the formal series. There are various types of generating functions, including ordinary generating functions, exponential generating functions, Lambert series, Bell series, and Dirichlet series. Every sequence in principle has a generating function of each type (except that Lambert and Dirichlet series require indices to start at 1 rather than 0), but the ease with which they can be handled may differ considerably. The particular generating function, if any, that is most useful in a given context will depend upon the nature of the sequence and the details of the problem being addressed. Generating functions are sometimes called generating series, in that a series of terms can be said to be the generator of its sequence ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fibonacci Number
In mathematics, the Fibonacci sequence is a Integer sequence, sequence in which each element is the sum of the two elements that precede it. Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers, commonly denoted . Many writers begin the sequence with 0 and 1, although some authors start it from 1 and 1 and some (as did Fibonacci) from 1 and 2. Starting from 0 and 1, the sequence begins : 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... The Fibonacci numbers were first described in Indian mathematics as early as 200 BC in work by Pingala on enumerating possible patterns of Sanskrit poetry formed from syllables of two lengths. They are named after the Italian mathematician Leonardo of Pisa, also known as Fibonacci, who introduced the sequence to Western European mathematics in his 1202 book . Fibonacci numbers appear unexpectedly often in mathematics, so much so that there is an entire journal dedicated to their study, the ''Fibonacci Quarterly''. Appli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
George Andrews (mathematician)
George Eyre Andrews (born December 4, 1938) is an American mathematician working in special functions, number theory, analysis and combinatorics. Education and career He is currently an Evan Pugh Professor of Mathematics at Pennsylvania State University. He did his undergraduate studies at Oregon State University and received his PhD in 1964 at the University of Pennsylvania where his advisor was Hans Rademacher. During 2008–2009 he was president of the American Mathematical Society. Contributions Andrews's contributions include several monographs and over 250 research and popular articles on q-series, special functions, combinatorics and applications. He is considered to be the world's leading expert in the theory of integer partitions. In 1976 he discovered Ramanujan's Lost Notebook. He is interested in mathematical pedagogy. His book ''The Theory of Partitions'' is the standard reference on the subject of integer partitions. He has advanced mathematics in the theories o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
King (chess)
The king (♔, ♚) is the most important chess piece, piece in the game of chess. It may move to any adjoining square; it may also perform, in tandem with the Rook (chess), rook, a special move called ''castling''. If a player's king is threatened with capture, it is said to be ''in Check (chess), check'', and the player must remove or evade the threat of immediately, such as by moving it away from the attacked square. If this cannot be done, the king is said to be in checkmate, resulting in a loss for that player. A player cannot make any move that places their own king in check. Despite this, the king can become a strong offensive piece in the Chess endgame, endgame or, rarely, the Chess middlegame, middlegame. In Algebraic notation (chess), algebraic notation, the king is abbreviated by the letter ''K'' among English speakers. The white king starts the game on e1; the black king starts on e8. Unlike all other pieces, each player can have only one king, and the kings are never ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chess
Chess is a board game for two players. It is an abstract strategy game that involves Perfect information, no hidden information and no elements of game of chance, chance. It is played on a square chessboard, board consisting of 64 squares arranged in an 8×8 grid. The players, referred to as White and Black in chess, "White" and "Black", each control sixteen Chess piece, pieces: one king (chess), king, one queen (chess), queen, two rook (chess), rooks, two bishop (chess), bishops, two knight (chess), knights, and eight pawn (chess), pawns, with each type of piece having a different pattern of movement. An enemy piece may be captured (removed from the board) by moving one's own piece onto the square it occupies. The object of the game is to "checkmate" (threaten with inescapable capture) the enemy king. There are also several ways a game can end in a draw (chess), draw. The recorded history of chess goes back to at least the emergence of chaturanga—also thought to be an ancesto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |