|
Trace Theory
Trace may refer to: Arts and entertainment Music * ''Trace'' (Son Volt album), 1995 * ''Trace'' (Died Pretty album), 1993 * Trace (band), a Dutch progressive rock band * ''The Trace'' (album), by Nell Other uses in arts and entertainment * ''Trace'' (magazine), British hip-hop magazine * ''Trace'' (manhwa), a Korean internet cartoon * ''Trace'' (manga), a Japanese manga series by Kei Koga * ''Trace'' (novel), a novel by Patricia Cornwell * ''The Trace'' (film), a 1994 Turkish film * ''The Trace'' (video game), 2015 video game * ''Sama'' (film), alternate title ''The Trace'', a 1988 Tunisian film * Trace, a fictional character in the game '' Metroid Prime Hunters'' * Trace, the protagonist of '' Axiom Verge'' * Trace, another name for Portgas D. Ace, a fictional character in the manga ''One Piece'' * Trace, the main brand for a number of music channels such as Trace Urban Language * Trace (deconstruction), a concept in Derridian deconstruction * Trace (linguistics), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Disambiguation Dos And Don'ts
Word-sense disambiguation is the process of identifying which word sense, sense of a word is meant in a sentence (linguistics), sentence or other segment of context (language use), context. In human language processing in the brain, language processing and cognition, it is usually subconscious. Given that natural language requires reflection of neurological reality, as shaped by the abilities provided by the brain's biological neural network, neural networks, computer science has had a long-term challenge in developing the ability in computers to do natural language processing and machine learning. Many techniques have been researched, including dictionary-based methods that use the knowledge encoded in lexical resources, supervised machine learning methods in which a classifier (mathematics), classifier is trained for each distinct word on a Corpus linguistics, corpus of manually sense-annotated examples, and completely unsupervised methods that cluster occurrences of words, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
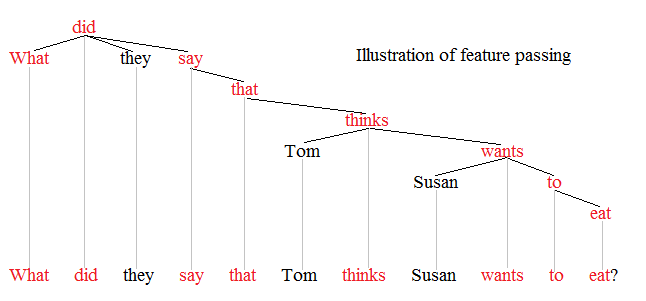
Trace (linguistics)
Syntactic movement is the means by which some theories of syntax address discontinuities. Movement was first postulated by structuralist linguists who expressed it in terms of ''discontinuous constituents'' or ''displacement''. Some constituents appear to have been displaced from the position in which they receive important features of interpretation. The concept of movement is controversial and is associated with so-called ''transformational'' or ''derivational'' theories of syntax (such as transformational grammar, government and binding theory, minimalist program). Representational theories (such as head-driven phrase structure grammar, lexical functional grammar, construction grammar, and most dependency grammars), in contrast, reject the notion of movement and often instead address discontinuities with other mechanisms including graph reentrancies, feature passing, and type shifters. Illustration Movement is the traditional means of explaining discontinuities such as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Field Trace
In mathematics, the field trace is a particular function defined with respect to a finite field extension ''L''/''K'', which is a ''K''-linear map from ''L'' onto ''K''. Definition Let ''K'' be a field and ''L'' a finite extension (and hence an algebraic extension) of ''K''. ''L'' can be viewed as a vector space over ''K''. Multiplication by ''α'', an element of ''L'', :m_\alpha:L\to L \text m_\alpha (x) = \alpha x, is a ''K''- linear transformation of this vector space into itself. The ''trace'', Tr''L''/''K''(''α''), is defined as the trace (in the linear algebra sense) of this linear transformation. For ''α'' in ''L'', let ''σ''(''α''), ..., ''σ''(''α'') be the roots (counted with multiplicity) of the minimal polynomial of ''α'' over ''K'' (in some extension field of ''K''). Then :\operatorname_(\alpha) = :K(\alpha)sum_^n\sigma_j(\alpha). If ''L''/''K'' is separable then each root appears only once (however this does not mean the coefficient above is one; for e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Trace (linear Algebra)
In linear algebra, the trace of a square matrix , denoted , is the sum of the elements on its main diagonal, a_ + a_ + \dots + a_. It is only defined for a square matrix (). The trace of a matrix is the sum of its eigenvalues (counted with multiplicities). Also, for any matrices and of the same size. Thus, similar matrices have the same trace. As a consequence, one can define the trace of a linear operator mapping a finite-dimensional vector space into itself, since all matrices describing such an operator with respect to a basis are similar. The trace is related to the derivative of the determinant (see Jacobi's formula). Definition The trace of an square matrix is defined as \operatorname(\mathbf) = \sum_^n a_ = a_ + a_ + \dots + a_ where denotes the entry on the row and column of . The entries of can be real numbers, complex numbers, or more generally elements of a field . The trace is not defined for non-square matrices. Example Let be a matrix, with \m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Trace Table
A trace table is a technique used to test algorithms in order to make sure that no logical errors occur while the calculations are being processed. The table usually takes the form of a multi-column, multi-row table; With each column showing a variable, and each row showing each number input into the algorithm and the subsequent values of the variables. Trace tables are typically used in schools and colleges when teaching students how to program. They can be an essential tool in teaching students how certain calculations work and the systematic process that is occurring when an algorithm is executed. They can also be useful for debugging applications, helping the programmer to easily detect what error is occurring, and why it may be occurring. Example int i, x = 0; for (i = 1; i <= 10; i++) This example shows the systematic process that takes place whilst the algorithm is processed. The initial value of ''x'' is zero, but ''i'', although defined, has no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Trace Cache
In computer architecture, a trace cache or execution trace cache is a specialized instruction cache which stores the dynamic stream of instructions known as trace. It helps in increasing the instruction fetch bandwidth and decreasing power consumption (in the case of Intel Pentium 4) by storing traces of instructions that have already been fetched and decoded. A trace processor is an architecture designed around the trace cache and processes the instructions at trace level granularity. The formal mathematical theory of traces is described by trace monoids. Background The earliest academic publication of trace cache was "Trace Cache: a Low Latency Approach to High Bandwidth Instruction Fetching". This widely acknowledged paper was presented by Eric Rotenberg, Steve Bennett, and Jim Smith at 1996 International Symposium on Microarchitecture (MICRO) conference. An earlier publication is US patent 5381533, by Alex Peleg and Uri Weiser of Intel, "Dynamic flow instruction cache me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Stack Trace
In computing, a stack trace (also called stack backtrace or stack traceback) is a report of the active stack frames at a certain point in time during the execution of a program. When a program is run, memory is often dynamically allocated in two places: the stack and the heap. Memory is continuously allocated on a stack but not on a heap. Stack also refers to a programming construct, thus to differentiate it, this stack is referred to as the program's function call stack. Technically, once a block of memory has been allocated on the stack, it cannot be easily removed as there can be other blocks of memory that were allocated after it. Each time a function is called in a program, a block of memory called an activation record is allocated on top of the call stack. Generally, the activation record stores the function's arguments and local variables. What exactly it contains and how it's laid out is determined by the calling convention. Programmers commonly use stack tracing dur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Signal Trace
In electronics, a signal trace or circuit trace on a printed circuit board (PCB) or integrated circuit (IC) is the equivalent of a wire for conducting signals. Each trace consists of a flat, narrow part of the copper Copper is a chemical element; it has symbol Cu (from Latin ) and atomic number 29. It is a soft, malleable, and ductile metal with very high thermal and electrical conductivity. A freshly exposed surface of pure copper has a pinkish-orang ... foil that remains after etching. Signal traces are usually narrower than power or ground traces because the current carrying requirements are usually much less. See also * Ground plane * Stripline * Microstrip References Electrical connectors Printed circuit board manufacturing {{electronics-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Packet Analyzer
A packet analyzer (also packet sniffer or network analyzer) is a computer program or computer hardware such as a packet capture appliance that can analyze and log traffic that passes over a computer network or part of a network. Packet capture is the process of intercepting and logging traffic. As data streams flow across the network, the analyzer captures each packet and, if needed, decodes the packet's raw data, showing the values of various fields in the packet, and analyzes its content according to the appropriate RFC or other specifications. A packet analyzer used for intercepting traffic on wireless networks is known as a wireless analyzer - those designed specifically for Wi-Fi networks are Wi-Fi analyzers. While a packet analyzer can also be referred to as a network analyzer or protocol analyzer these terms can also have other meanings. Protocol analyzer can technically be a broader, more general class that includes packet analyzers/sniffers. However, the terms a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Digital Traces
Digital footprint or digital shadow refers to one's unique set of traceable digital activities, actions, contributions, and communications manifested on the Internet or digital devices. Digital footprints can be classified as either passive or active. Passive footprints consist of a user's web-browsing activity and information stored as cookies. Active footprints are intentionally created by users to share information on websites or social media. While the term usually applies to a person, a digital footprint can also refer to a business, organization or corporation. The use of a digital footprint has both positive and negative consequences. On one side, it is the subject of many privacy issues. For example, without an individual's authorization, strangers can piece together information about that individual by only using search engines. Social inequalities are exacerbated by the limited access afforded to marginalized communities. Corporations are also able to produce cust ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Trace Monoid
In computer science, a trace is an equivalence class of strings, wherein certain letters in the string are allowed to commute, but others are not. Traces generalize the concept of strings by relaxing the requirement for all the letters to have a definite order, instead allowing for indefinite orderings in which certain reshufflings could take place. In an opposite way, traces generalize the concept of sets with multiplicities by allowing for specifying some incomplete ordering of the letters rather than requiring complete equivalence under all reorderings. The trace monoid or free partially commutative monoid is a monoid of traces. Traces were introduced by Pierre Cartier and Dominique Foata in 1969 to give a combinatorial proof of MacMahon's master theorem. Traces are used in theories of concurrent computation, where commuting letters stand for portions of a job that can execute independently of one another, while non-commuting letters stand for locks, synchronization poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hypertext Transfer Protocol
HTTP (Hypertext Transfer Protocol) is an application layer protocol in the Internet protocol suite model for distributed, collaborative, hypermedia information systems. HTTP is the foundation of data communication for the World Wide Web, where hypertext documents include hyperlinks to other resources that the user can easily access, for example by a mouse click or by tapping the screen in a web browser. Development of HTTP was initiated by Tim Berners-Lee at CERN in 1989 and summarized in a simple document describing the behavior of a client and a server using the first HTTP version, named 0.9. That version was subsequently developed, eventually becoming the public 1.0. Development of early HTTP Requests for Comments (RFCs) started a few years later in a coordinated effort by the Internet Engineering Task Force (IETF) and the World Wide Web Consortium (W3C), with work later moving to the IETF. HTTP/1 was finalized and fully documented (as version 1.0) in 1996. It evolved ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |