|
Toroidal Ring Model
The toroidal ring model, known originally as the Parson magneton or magnetic electron, is a physical model of subatomic particles. It is also known as the plasmoid ring, vortex ring, or helicon ring. This physical model treated electrons and protons as elementary particles, and was first proposed by Alfred Lauck Parson in 1915. Theory Instead of a single orbiting charge, the toroidal ring was conceived as a collection of infinitesimal charge elements, which orbited or circulated along a common continuous path or " loop". In general, this path of charge could assume any shape, but tended toward a circular form due to internal repulsive electromagnetic forces. In this configuration the charge elements circulated, but the ring as a whole did not radiate due to changes in electric or magnetic fields since it remained stationary. The ring produced an overall magnetic field (" spin") due to the current of the moving charge elements. These elements circulated around the ring a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Toroid (geometry)
In mathematics, a toroid is a surface of revolution with a hole in the middle. The axis of revolution passes through the hole and so does not intersect the surface. For example, when a rectangle is rotated around an axis parallel to one of its edges, then a hollow rectangle-section ring is produced. If the revolved figure is a circle, then the object is called a torus. The term ''toroid'' is also used to describe a toroidal polyhedron. In this context a toroid need not be circular and may have any number of holes. A ''g''-holed ''toroid'' can be seen as approximating the surface of a torus having a topological genus, ''g'', of 1 or greater. The Euler characteristic χ of a ''g'' holed toroid is 2(1−''g''). The torus is an example of a toroid, which is the surface of a doughnut. Doughnuts are an example of a solid torus created by rotating a disk, and are not toroids. Toroidal structures occur in both natural and synthetic materials. Equations A toroid is specified b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Field (physics)
In science, a field is a physical quantity, represented by a scalar (mathematics), scalar, vector (mathematics and physics), vector, or tensor, that has a value for each Point (geometry), point in Spacetime, space and time. An example of a scalar field is a weather map, with the surface temperature described by assigning a real number, number to each point on the map. A surface wind map, assigning an arrow to each point on a map that describes the wind velocity, speed and direction at that point, is an example of a vector field, i.e. a 1-dimensional (rank-1) tensor field. Field theories, mathematical descriptions of how field values change in space and time, are ubiquitous in physics. For instance, the electric field is another rank-1 tensor field, while electrodynamics can be formulated in terms of Mathematical descriptions of the electromagnetic field, two interacting vector fields at each point in spacetime, or as a Covariant formulation of classical electromagnetism, single-ra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proportionality Constant
In mathematics, two sequences of numbers, often experimental data, are proportional or directly proportional if their corresponding elements have a constant ratio. The ratio is called ''coefficient of proportionality'' (or ''proportionality constant'') and its reciprocal is known as ''constant of normalization'' (or ''normalizing constant''). Two sequences are inversely proportional if corresponding elements have a constant product. Two functions f(x) and g(x) are ''proportional'' if their ratio \frac is a constant function. If several pairs of variables share the same direct proportionality constant, the equation expressing the equality of these ratios is called a proportion, e.g., (for details see Ratio). Proportionality is closely related to ''linearity''. Direct proportionality Given an independent variable ''x'' and a dependent variable ''y'', ''y'' is directly proportional to ''x'' if there is a positive constant ''k'' such that: : y = kx The relation is often ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proportionality (mathematics)
In mathematics, two sequences of numbers, often experimental data, are proportional or directly proportional if their corresponding elements have a constant ratio. The ratio is called ''coefficient of proportionality'' (or ''proportionality constant'') and its reciprocal is known as ''constant of normalization'' (or ''normalizing constant''). Two sequences are inversely proportional if corresponding elements have a constant product. Two functions f(x) and g(x) are ''proportional'' if their ratio \frac is a constant function. If several pairs of variables share the same direct proportionality constant, the equation expressing the equality of these ratios is called a proportion, e.g., (for details see Ratio). Proportionality is closely related to ''linearity''. Direct proportionality Given an independent variable ''x'' and a dependent variable ''y'', ''y'' is directly proportional to ''x'' if there is a positive constant ''k'' such that: : y = kx The relation is oft ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spring (device)
A spring is a device consisting of an Elasticity (physics), elastic but largely rigid material (typically metal) bent or molded into a form (especially a coil) that can return into shape after being compressed or extended. Springs can Energy storage, store energy when compressed. In everyday use, the term most often refers to coil springs, but there are many different spring designs. Modern springs are typically manufactured from spring steel. An example of a non-metallic spring is the Bow (weapon), bow, made traditionally of flexible Taxus baccata, yew wood, which when Bow draw, drawn stores energy to propel an arrow. When a conventional spring, without stiffness variability features, is compressed or stretched from its resting position, it exerts an opposing force approximately proportional to its change in length (this approximation breaks down for larger deflections). The ''rate'' or ''spring constant'' of a spring is the change in the force it exerts, divided by the cha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compression (physical)
In mechanics, compression is the application of balanced inward ("pushing") forces to different points on a material or structure, that is, forces with no net sum or torque directed so as to reduce its size in one or more directions.Ferdinand Pierre Beer, Elwood Russell Johnston, John T. DeWolf (1992), "Mechanics of Materials". (Book) McGraw-Hill Professional, It is contrasted with tension or traction, the application of balanced outward ("pulling") forces; and with shearing forces, directed so as to displace layers of the material parallel to each other. The compressive strength of materials and structures is an important engineering consideration. In uniaxial compression, the forces are directed along one direction only, so that they act towards decreasing the object's length along that direction. The compressive forces may also be applied in multiple directions; for example inwards along the edges of a plate or all over the side surface of a cylinder, so as to reduce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Energy
Energy () is the physical quantity, quantitative physical property, property that is transferred to a physical body, body or to a physical system, recognizable in the performance of Work (thermodynamics), work and in the form of heat and light. Energy is a Conservation law, conserved quantity—the law of conservation of energy states that energy can be Energy transformation, converted in form, but not created or destroyed. The unit of measurement for energy in the International System of Units (SI) is the joule (J). Forms of energy include the kinetic energy of a moving object, the potential energy stored by an object (for instance due to its position in a Classical field theory, field), the elastic energy stored in a solid object, chemical energy associated with chemical reactions, the radiant energy carried by electromagnetic radiation, the internal energy contained within a thermodynamic system, and rest energy associated with an object's rest mass. These are not mutual ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inertia
Inertia is the natural tendency of objects in motion to stay in motion and objects at rest to stay at rest, unless a force causes the velocity to change. It is one of the fundamental principles in classical physics, and described by Isaac Newton in his Newton%27s_laws_of_motion#First, first law of motion (also known as The Principle of Inertia). It is one of the primary manifestations of mass, one of the core quantitative properties of physical systems. Newton writes: In his 1687 work ''Philosophiæ Naturalis Principia Mathematica'', Newton defined inertia as a property: History and development Early understanding of inertial motion Joseph NeedhamProfessor John H. Lienhard points out the Mozi (book), Mozi – based on a Chinese text from the Warring States period (475–221 BCE) – as having given the first description of inertia. Before the European Renaissance, the prevailing theory of motion in western philosophy was that of Aristotle (384–322 BCE). On the surface ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radius
In classical geometry, a radius (: radii or radiuses) of a circle or sphere is any of the line segments from its Centre (geometry), center to its perimeter, and in more modern usage, it is also their length. The radius of a regular polygon is the line segment or distance from its center to any of its Vertex (geometry), vertices. The name comes from the Latin ''radius'', meaning ray but also the spoke of a chariot wheel.Definition of Radius at dictionary.reference.com. Accessed on 2009-08-08. The typical abbreviation and mathematical symbol for radius is ''R'' or ''r''. By extension, the diameter ''D'' is defined as twice the radius:Definition of radius at mathwords.com. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
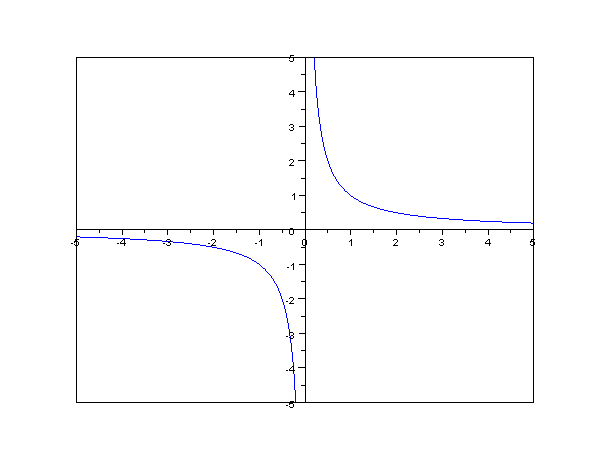
Inversely Proportional
In mathematics, two sequences of numbers, often experimental data, are proportional or directly proportional if their corresponding elements have a constant ratio. The ratio is called ''coefficient of proportionality'' (or ''proportionality constant'') and its reciprocal is known as ''constant of normalization'' (or ''normalizing constant''). Two sequences are inversely proportional if corresponding elements have a constant product. Two functions f(x) and g(x) are ''proportional'' if their ratio \frac is a constant function. If several pairs of variables share the same direct proportionality constant, the equation expressing the equality of these ratios is called a proportion, e.g., (for details see Ratio). Proportionality is closely related to ''linearity''. Direct proportionality Given an independent variable ''x'' and a dependent variable ''y'', ''y'' is directly proportional to ''x'' if there is a positive constant ''k'' such that: : y = kx The relation is ofte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency
Frequency is the number of occurrences of a repeating event per unit of time. Frequency is an important parameter used in science and engineering to specify the rate of oscillatory and vibratory phenomena, such as mechanical vibrations, audio signals (sound), radio waves, and light. The interval of time between events is called the period. It is the reciprocal of the frequency. For example, if a heart beats at a frequency of 120 times per minute (2 hertz), its period is one half of a second. Special definitions of frequency are used in certain contexts, such as the angular frequency in rotational or cyclical properties, when the rate of angular progress is measured. Spatial frequency is defined for properties that vary or cccur repeatedly in geometry or space. The unit of measurement of frequency in the International System of Units (SI) is the hertz, having the symbol Hz. Definitions and units For cyclical phenomena such as oscillations, waves, or for examp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Speed Of Light
The speed of light in vacuum, commonly denoted , is a universal physical constant exactly equal to ). It is exact because, by international agreement, a metre is defined as the length of the path travelled by light in vacuum during a time interval of second. The speed of light is invariant (physics), the same for all observers, no matter their relative velocity. It is the upper limit for the speed at which Information#Physics_and_determinacy, information, matter, or energy can travel through Space#Relativity, space. All forms of electromagnetic radiation, including visible light, travel at the speed of light. For many practical purposes, light and other electromagnetic waves will appear to propagate instantaneously, but for long distances and sensitive measurements, their finite speed has noticeable effects. Much starlight viewed on Earth is from the distant past, allowing humans to study the history of the universe by viewing distant objects. When Data communication, comm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |