|
Thomson's Lamp
Thomson's lamp is a philosophical puzzle based on infinites. It was devised in 1954 by British philosopher James F. Thomson, who used it to analyze the possibility of a supertask, which is the completion of an infinite number of tasks. Consider a lamp with a toggle switch. Flicking the switch once turns the lamp on. Another flick will turn the lamp off. Now suppose that there is a being who is able to perform the following task: starting a timer, he turns the lamp on. At the end of one minute, he turns it off. At the end of another half minute, he turns it on again. At the end of another quarter of a minute, he turns it off. At the next eighth of a minute, he turns it on again, and he continues thus, flicking the switch each time after waiting exactly one-half the time he waited before flicking it previously. The sum of this infinite series of time intervals is exactly two minutes. The following question is then considered: Is the lamp on or off at two minutes? Thomson ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Puzzle
A puzzle is a game, problem, or toy that tests a person's ingenuity or knowledge. In a puzzle, the solver is expected to put pieces together ( or take them apart) in a logical way, in order to arrive at the correct or fun solution of the puzzle. There are different genres of puzzles, such as crossword puzzles, word-search puzzles, number puzzles, relational puzzles, and logic puzzles. The academic study of puzzles is called enigmatology. Puzzles are often created to be a form of entertainment but they can also arise from serious mathematical or logical problems. In such cases, their solution may be a significant contribution to mathematical research. Etymology The ''Oxford English Dictionary'' dates the word ''puzzle'' (as a verb) to the end of the 16th century. Its earliest use documented in the ''OED'' was in a book titled ''The Voyage of Robert Dudley...to the West Indies, 1594–95, narrated by Capt. Wyatt, by himself, and by Abram Kendall, master'' (published circa 1595) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transfinite Numbers
In mathematics, transfinite numbers are numbers that are "infinite" in the sense that they are larger than all finite numbers, yet not necessarily absolutely infinite. These include the transfinite cardinals, which are cardinal numbers used to quantify the size of infinite sets, and the transfinite ordinals, which are ordinal numbers used to provide an ordering of infinite sets. The term ''transfinite'' was coined by Georg Cantor in 1895, who wished to avoid some of the implications of the word ''infinite'' in connection with these objects, which were, nevertheless, not ''finite''. Few contemporary writers share these qualms; it is now accepted usage to refer to transfinite cardinals and ordinals as infinite numbers. Nevertheless, the term "transfinite" also remains in use. Definition Any finite natural number can be used in at least two ways: as an ordinal and as a cardinal. Cardinal numbers specify the size of sets (e.g., a bag of five marbles), whereas ordinal numbers specify t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
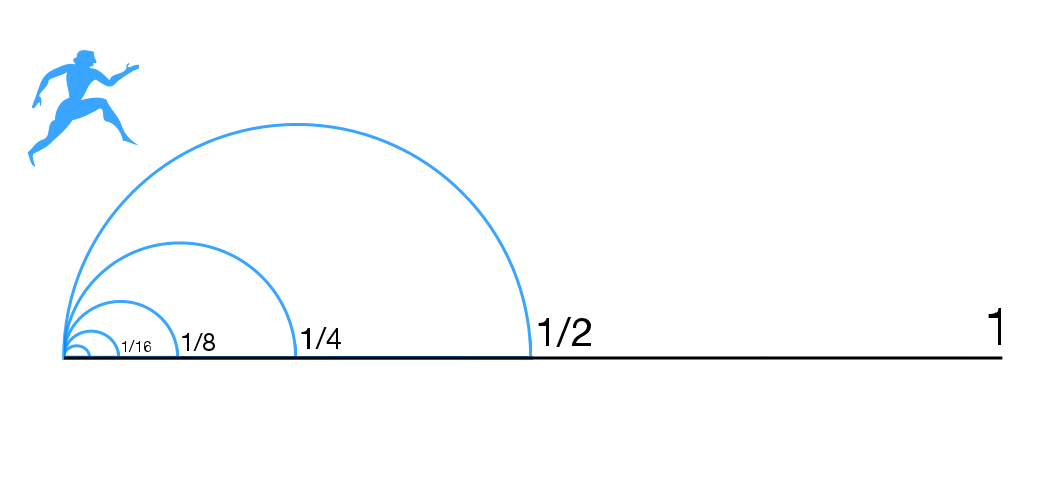
Supertasks
In philosophy, a supertask is a countably infinite sequence of operations that occur sequentially within a finite interval of time. Supertasks are called hypertasks when the number of operations becomes uncountably infinite. A hypertask that includes one task for each ordinal number is called an ultratask. The term "supertask" was coined by the philosopher James F. Thomson, who devised Thomson's lamp. The term "hypertask" derives from Clark and Read in their paper of that name. History Zeno Motion The origin of the interest in supertasks is normally attributed to Zeno of Elea. Zeno claimed that motion was impossible. He argued as follows: suppose our burgeoning "mover", Achilles say, wishes to move from A to B. To achieve this he must traverse half the distance from A to B. To get from the midpoint of AB to B, Achilles must traverse half ''this'' distance, and so on and so forth. However many times he performs one of these "traversing" tasks, there is another one left for him ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zeno Machine
In mathematics and computer science, Zeno machines (abbreviated ZM, and also called accelerated Turing machine, ATM) are a hypothetical computational model related to Turing machines that are capable of carrying out computations involving a countably infinite number of algorithmic steps. These machines are ruled out in most models of computation. The idea of Zeno machines was first discussed by Hermann Weyl in 1927; the name refers to Zeno's paradoxes, attributed to the ancient Greek philosopher Zeno of Elea. Zeno machines play a crucial role in some theories. The theory of the Omega Point devised by physicist Frank J. Tipler, for instance, can only be valid if Zeno machines are possible. Definition A Zeno machine is a Turing machine that can take a infinite number of steps, and then continue take more steps. This can be thought of as a supertask where 1/2^n units of time are taken to perform the n-th step; thus, the first step takes 0.5 units of time, the second takes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zeno's Paradoxes
Zeno's paradoxes are a set of philosophical problems generally thought to have been devised by Greek philosopher Zeno of Elea (c. 490–430 BC) to support Parmenides' doctrine that contrary to the evidence of one's senses, the belief in plurality and change is mistaken, and in particular that motion is nothing but an illusion. It is usually assumed, based on Plato's ''Parmenides'' (128a–d), that Zeno took on the project of creating these paradoxes because other philosophers had created paradoxes against Parmenides' view. Thus Plato has Zeno say the purpose of the paradoxes "is to show that their hypothesis that existences are many, if properly followed up, leads to still more absurd results than the hypothesis that they are one." Plato has Socrates claim that Zeno and Parmenides were essentially arguing exactly the same point. Some of Zeno's nine surviving paradoxes (preserved in Aristotle's ''Physics'' [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ross–Littlewood Paradox
The Ross–Littlewood paradox (also known as the balls and vase problem or the ping pong ball problem) is a hypothetical problem in abstract mathematics and logic designed to illustrate the paradoxical, or at least non-intuitive, nature of infinity. More specifically, like the Thomson's lamp paradox, the Ross–Littlewood paradox tries to illustrate the conceptual difficulties with the notion of a supertask, in which an infinite number of tasks are completed sequentially. The problem was originally described by mathematician John E. Littlewood in his 1953 book ''Littlewood's Miscellany'', and was later expanded upon by Sheldon Ross in his 1988 book ''A First Course in Probability''. The problem starts with an empty vase and an infinite supply of balls. An infinite number of steps are then performed, such that at each step 10 balls are added to the vase and 1 ball removed from it. The question is then posed: ''How many balls are in the vase when the task is finished?'' To comple ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Paradoxes
This list includes well known paradoxes, grouped thematically. The grouping is approximate, as paradoxes may fit into more than one category. This list collects only scenarios that have been called a paradox by at least one source and have their own article in this encyclopedia. Although considered paradoxes, some of these are simply based on fallacious reasoning (falsidical), or an unintuitive solution ( veridical). Informally, the term ''paradox'' is often used to describe a counter-intuitive result. However, some of these paradoxes qualify to fit into the mainstream perception of a paradox, which is a self-contradictory result gained even while properly applying accepted ways of reasoning. These paradoxes, often called '' antinomy,'' point out genuine problems in our understanding of the ideas of truth and description. Logic * : The supposition that, 'if one of two simultaneous assumptions leads to a contradiction, the other assumption is also disproved' leads to paradoxica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
History Of Grandi's Series
Geometry and infinite zeros Grandi Guido Grandi (1671–1742) reportedly provided a simplistic account of the series in 1703. He noticed that inserting parentheses into produced varying results: either :(1-1) + (1-1) + \cdots = 0 or :1+(-1+1)+(-1+1) +\cdots = 1. Grandi's explanation of this phenomenon became well known for its religious overtones: In fact, the series was not an idle subject for Grandi, and he didn't think it summed to either 0 or 1. Rather, like many mathematicians to follow, he thought the true value of the series was 1⁄2 for a variety of reasons. Grandi's mathematical treatment of occurs in his 1703 book ''Quadratura circula et hyperbolae per infinitas hyperbolas geometrice exhibita''. Broadly interpreting Grandi's work, he derived through geometric reasoning connected with his investigation of the witch of Agnesi. Eighteenth-century mathematicians immediately translated and summarized his argument in analytical terms: for a generating circle with di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cesàro Summation
In mathematical analysis, Cesàro summation (also known as the Cesàro mean ) assigns values to some infinite sums that are not necessarily convergent in the usual sense. The Cesàro sum is defined as the limit, as ''n'' tends to infinity, of the sequence of arithmetic means of the first ''n'' partial sums of the series. This special case of a matrix summability method is named for the Italian analyst Ernesto Cesàro (1859–1906). The term ''summation'' can be misleading, as some statements and proofs regarding Cesàro summation can be said to implicate the Eilenberg–Mazur swindle. For example, it is commonly applied to Grandi's series with the conclusion that the ''sum'' of that series is 1/2. Definition Let (a_n)_^\infty be a sequence, and let :s_k = a_1 + \cdots + a_k= \sum_^k a_n be its th partial sum. The sequence is called Cesàro summable, with Cesàro sum , if, as tends to infinity, the arithmetic mean of its first ''n'' partial sums tends to : :\lim_ \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
James F
James is a common English language surname and given name: *James (name), the typically masculine first name James * James (surname), various people with the last name James James or James City may also refer to: People * King James (other), various kings named James * Saint James (other) * James (musician) * James, brother of Jesus Places Canada * James Bay, a large body of water * James, Ontario United Kingdom * James College, a college of the University of York United States * James, Georgia, an unincorporated community * James, Iowa, an unincorporated community * James City, North Carolina * James City County, Virginia ** James City (Virginia Company) ** James City Shire * James City, Pennsylvania * St. James City, Florida Arts, entertainment, and media * ''James'' (2005 film), a Bollywood film * ''James'' (2008 film), an Irish short film * ''James'' (2022 film), an Indian Kannada-language film * James the Red Engine, a character in ''Tho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit Of A Sequence
As the positive integer n becomes larger and larger, the value n\cdot \sin\left(\tfrac1\right) becomes arbitrarily close to 1. We say that "the limit of the sequence n\cdot \sin\left(\tfrac1\right) equals 1." In mathematics, the limit of a sequence is the value that the terms of a sequence "tend to", and is often denoted using the \lim symbol (e.g., \lim_a_n).Courant (1961), p. 29. If such a limit exists, the sequence is called convergent. A sequence that does not converge is said to be divergent. The limit of a sequence is said to be the fundamental notion on which the whole of mathematical analysis ultimately rests. Limits can be defined in any metric or topological space, but are usually first encountered in the real numbers. History The Greek philosopher Zeno of Elea is famous for formulating paradoxes that involve limiting processes. Leucippus, Democritus, Antiphon, Eudoxus, and Archimedes developed the method of exhaustion, which uses an infinite sequence ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sequence
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is called the ''length'' of the sequence. Unlike a set, the same elements can appear multiple times at different positions in a sequence, and unlike a set, the order does matter. Formally, a sequence can be defined as a function from natural numbers (the positions of elements in the sequence) to the elements at each position. The notion of a sequence can be generalized to an indexed family, defined as a function from an ''arbitrary'' index set. For example, (M, A, R, Y) is a sequence of letters with the letter 'M' first and 'Y' last. This sequence differs from (A, R, M, Y). Also, the sequence (1, 1, 2, 3, 5, 8), which contains the number 1 at two different positions, is a valid sequence. Sequences can be '' finite'', as in these examples, or '' i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |