|
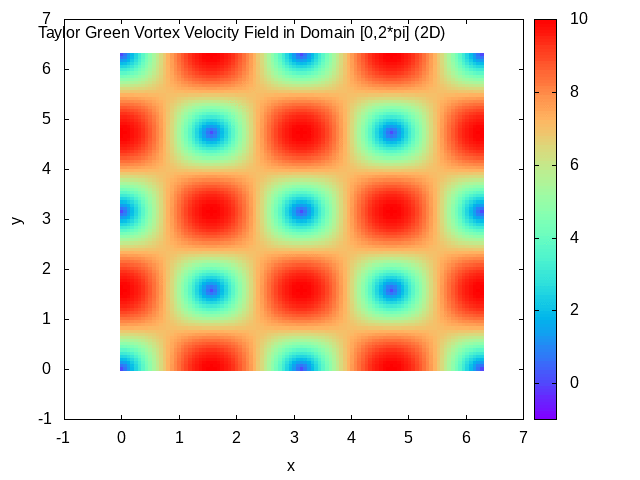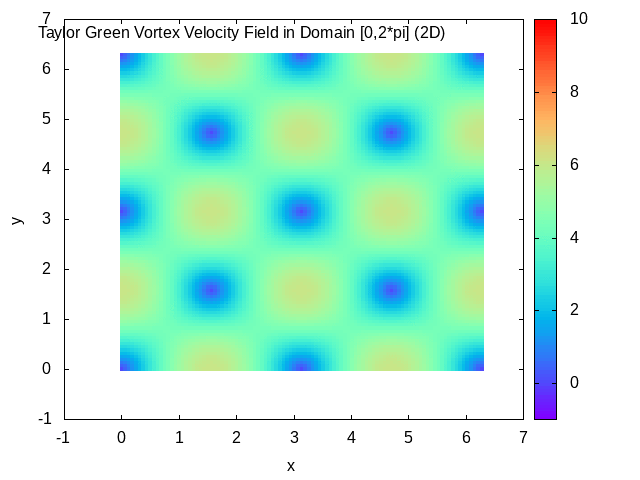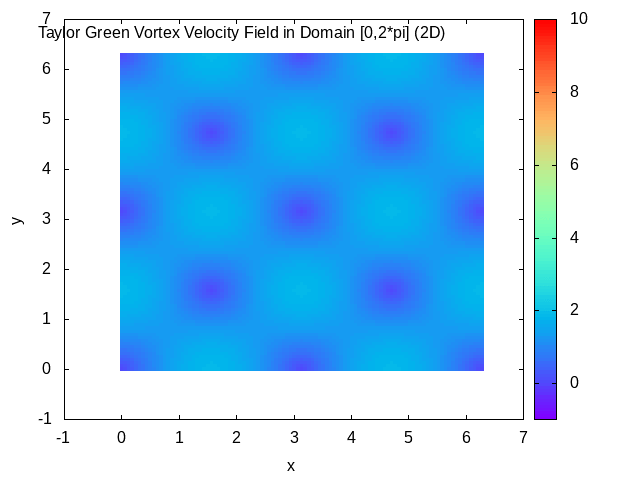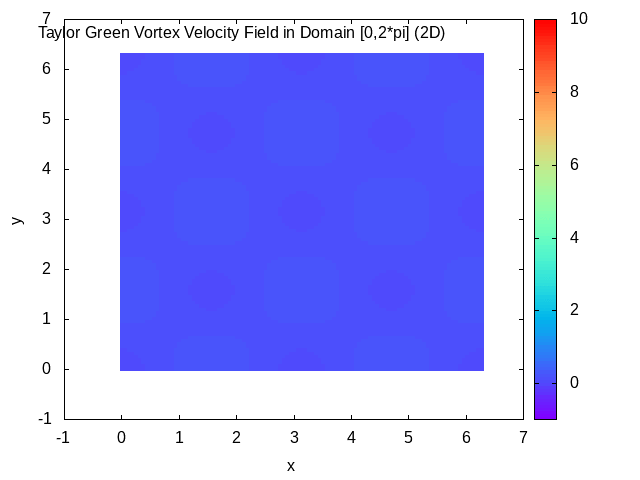
Taylor–Green Vortex
In fluid dynamics, the Taylor–Green vortex is an unsteady flow of a decaying vortex, which has an exact closed form solution of the incompressible Navier–Stokes equations in Cartesian coordinates. It is named after the British physicist and mathematician Geoffrey Ingram Taylor and his collaborator A. E. Green. Taylor, G. I. and Green, A. E., ''Mechanism of the Production of Small Eddies from Large Ones'', Proc. R. Soc. Lond. A, 158, 499–521 (1937). Original work In the original work of Taylor and Green, a particular flow is analyzed in three spatial dimensions, with the three velocity components \mathbf=(u,v,w) at time t=0 specified by : u = A \cos ax \sin by \sin cz, : v = B \sin ax \cos by \sin cz, : w = C \sin ax \sin by \cos cz. The continuity equation \nabla \cdot \mathbf=0 determines that Aa+Bb+Cc=0. The small time behavior of the flow is then found through simplification of the incompressible Navier–Stokes equations using the initial flow to give a step- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Green Vortex
Taylor, Taylors or Taylor's may refer to: People * Taylor (surname) **List of people with surname Taylor * Taylor (given name), including Tayla and Taylah * Taylor sept, a branch of Scottish clan Cameron * Justice Taylor (other) Places Australia * Electoral district of Taylor, South Australia * Taylor, Australian Capital Territory, planned suburb Canada * Taylor, British Columbia United States * Taylor, Alabama * Taylor, Arizona * Taylor, Arkansas * Taylor, Indiana * Taylor, Louisiana * Taylor, Maryland * Taylor, Michigan * Taylor, Mississippi * Taylor, Missouri * Taylor, Nebraska * Taylor, North Dakota * Taylor, New York * Taylor, Beckham County, Oklahoma * Taylor, Cotton County, Oklahoma * Taylor, Pennsylvania * Taylors, South Carolina * Taylor, Texas * Taylor, Utah * Taylor, Washington * Taylor, West Virginia * Taylor, Wisconsin * Taylor, Wyoming * Taylor County (other) * Taylor Township (other) Businesses and organisations * Taylor's (de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuity Equation
A continuity equation or transport equation is an equation that describes the transport of some quantity. It is particularly simple and powerful when applied to a conserved quantity, but it can be generalized to apply to any extensive quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described using continuity equations. Continuity equations are a stronger, local form of conservation laws. For example, a weak version of the law of conservation of energy states that energy can neither be created nor destroyed—i.e., the total amount of energy in the universe is fixed. This statement does not rule out the possibility that a quantity of energy could disappear from one point while simultaneously appearing at another point. A stronger statement is that energy is ''locally'' conserved: energy can neither be created nor destroyed, ''nor'' can it " ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parviz Moin
Parviz Moin ( fa, پرویز معین ''Parviz Mo'in'' born October 23, 1952, Valandan, Shahreza, Iran) is a fluid dynamicist. He is the Franklin P. and Caroline M. Johnson Professor of Mechanical Engineering at Stanford University. Moin has been listed as an ISI Highly Cited author in engineering. Biography Moin is from Iran, and now lives in California. He received his Bachelor's degree in mechanical engineering from the University of Minnesota in 1974, his Master's degree in mathematics and his Master's and Ph.D degrees in mechanical engineering from Stanford in 1978. Moin became a naturalized U.S. citizen in 1981. He held the posts of National Research Council Fellow, Staff Scientist and Senior Staff Scientist at NASA Ames Research Center. He joined the Stanford faculty in September 1986. Research Moin pioneered the use of direct numerical simulation and large eddy simulation techniques for the study of turbulence physics, control and modelling concepts and has written wid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Kim (professor)
Jeongbin John Kim (born 1947) is the Rockwell International Distinguished Professor of mechanical and aerospace engineering in the UCLA Henry Samueli School of Engineering and Applied Science, since 1993. He currently resides in Calabasas, California. Personal and early life Kim was born in South Korea. He received his B.S. degree at Seoul National University in 1970; his M.S. at Brown University in 1974; and his Ph.D. at Stanford University in 1978. Career Prior to joining UCLA, Kim worked at NASA Ames Research Center, where he conducted research in the areas of turbulence and transition physics as a research scientist and Chief of Turbulence and Transition Physics Branch. His primary research interest is numerical simulation of transitional and turbulent flows, physics and control of turbulent flows, and numerical algorithms for computational science. Kim has been a pioneer in developing direct numerical simulation (DNS) and large eddy simulation (LES) as a reliable and r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alexandre Chorin
Alexandre Joel Chorin (born 25 June 1938) is an American mathematician known for his contributions to computational fluid mechanics, turbulence, and computational statistical mechanics. Chorin's work involves developing methods for solving physics and fluid mechanics problems computationally. His early work introduced several widely used numerical methods for solving the Navier-Stokes equations, including the method of artificial compressibility, the projection method, and vortex methods. He has made numerous contributions to turbulence theory. In recent years he has been developing methods for prediction in the face of uncertainty and for filtering and data assimilation. Career Chorin is a University Professor at the University of California, a Professor of Mathematics at the University of California, Berkeley and a Senior Scientist at the Lawrence Berkeley National Laboratory. Chorin received the Ing. Dipl. Physics degree from the EPFL (École Polytechnique Fédérale ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vorticity
In continuum mechanics, vorticity is a pseudovector field that describes the local spinning motion of a continuum near some point (the tendency of something to rotate), as would be seen by an observer located at that point and traveling along with the flow. It is an important quantity in the dynamical theory of fluids and provides a convenient framework for understanding a variety of complex flow phenomena, such as the formation and motion of vortex rings. Mathematically, the vorticity \vec is the curl of the flow velocity \vec: :\vec \equiv \nabla \times \vec\,, where \nabla is the nabla operator. Conceptually, \vec could be determined by marking parts of a continuum in a small neighborhood of the point in question, and watching their ''relative'' displacements as they move along the flow. The vorticity \vec would be twice the mean angular velocity vector of those particles relative to their center of mass, oriented according to the right-hand rule. In a two-dimensiona ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stream Function
The stream function is defined for incompressible ( divergence-free) flows in two dimensions – as well as in three dimensions with axisymmetry. The flow velocity components can be expressed as the derivatives of the scalar stream function. The stream function can be used to plot streamlines, which represent the trajectories of particles in a steady flow. The two-dimensional Lagrange stream function was introduced by Joseph Louis Lagrange in 1781. The Stokes stream function is for axisymmetrical three-dimensional flow, and is named after George Gabriel Stokes. Considering the particular case of fluid dynamics, the difference between the stream function values at any two points gives the volumetric flow rate (or volumetric flux) through a line connecting the two points. Since streamlines are tangent to the flow velocity vector of the flow, the value of the stream function must be constant along a streamline. The usefulness of the stream function lies in the fact that t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series, when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the mid-18th century. The partial sum formed by the first terms of a Taylor series is a polynomial of degree that is called the th Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally better as increases. Taylor's theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Viscosity
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water. Viscosity quantifies the internal frictional force between adjacent layers of fluid that are in relative motion. For instance, when a viscous fluid is forced through a tube, it flows more quickly near the tube's axis than near its walls. Experiments show that some stress (such as a pressure difference between the two ends of the tube) is needed to sustain the flow. This is because a force is required to overcome the friction between the layers of the fluid which are in relative motion. For a tube with a constant rate of flow, the strength of the compensating force is proportional to the fluid's viscosity. In general, viscosity depends on a fluid's state, such as its temperature, pressure, and rate of deformation. However, the dependence on some of these properties ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Body Force
In physics, a body force is a force that acts throughout the volume of a body. Springer site - Book 'Solid mechanics'preview paragraph 'Body forces'./ref> Forces due to gravity, electric fields and magnetic fields are examples of body forces. Body forces contrast with contact forces or surface forces which are exerted to the surface of an object. Normal forces and shear forces between objects are surface forces as they are exerted to the surface of an object. All cohesive surface attraction and contact forces between objects are also considered as surface forces. Fictitious forces such as the centrifugal force, Euler force, and the Coriolis effect are other examples of body forces. Definition Qualitative A body force is simply a type of force, and so it has the same dimensions as force, L] sup>−2. However, it is often convenient to talk about a body force in terms of either the force per unit volume or the force per unit mass. If the force per unit volume is of int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vortex
In fluid dynamics, a vortex ( : vortices or vortexes) is a region in a fluid in which the flow revolves around an axis line, which may be straight or curved. Vortices form in stirred fluids, and may be observed in smoke rings, whirlpools in the wake of a boat, and the winds surrounding a tropical cyclone, tornado or dust devil. Vortices are a major component of turbulent flow. The distribution of velocity, vorticity (the curl of the flow velocity), as well as the concept of circulation are used to characterise vortices. In most vortices, the fluid flow velocity is greatest next to its axis and decreases in inverse proportion to the distance from the axis. In the absence of external forces, viscous friction within the fluid tends to organise the flow into a collection of irrotational vortices, possibly superimposed to larger-scale flows, including larger-scale vortices. Once formed, vortices can move, stretch, twist, and interact in complex ways. A moving vortex carrie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lagrangian Trajectories Anumation Of A Taylor Green Vortex
Lagrangian may refer to: Mathematics * Lagrangian function, used to solve constrained minimization problems in optimization theory; see Lagrange multiplier ** Lagrangian relaxation, the method of approximating a difficult constrained problem with an easier problem having an enlarged feasible set ** Lagrangian dual problem, the problem of maximizing the value of the Lagrangian function, in terms of the Lagrange-multiplier variable; See Dual problem * Lagrangian, a functional whose extrema are to be determined in the calculus of variations * Lagrangian submanifold, a class of submanifolds in symplectic geometry * Lagrangian system, a pair consisting of a smooth fiber bundle and a Lagrangian density Physics * Lagrangian mechanics, a reformulation of classical mechanics * Lagrangian (field theory), a formalism in classical field theory * Lagrangian point, a position in an orbital configuration of two large bodies * Lagrangian coordinates, a way of describing the motions of particles of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |