|
Sylvester's Determinant Identity
In matrix theory, Sylvester's determinant identity is an identity useful for evaluating certain types of determinants. It is named after James Joseph Sylvester, who stated this identity without proof in 1851. Cited in Given an ''n''-by-''n'' matrix A, let \det(A) denote its determinant. Choose a pair :u =(u_1, \dots, u_m), v =(v_1, \dots, v_m) \subset (1, \dots, n) of ''m''-element ordered subsets of (1, \dots, n), where ''m'' ≤ ''n''. Let A^u_v denote the (''n''−''m'')-by-(''n''−''m'') submatrix of A obtained by deleting the rows in u and the columns in v. Define the auxiliary ''m''-by-''m'' matrix \tilde^u_v whose elements are equal to the following determinants : (\tilde^u_v)_ := \det(A^_), where uhat/math>, vhat/math> denote the ''m''−1 element subsets of u and v obtained by deleting the elements u_i and v_j, respectively. Then the following is Sylvester's determinantal identity (Sylvester, 1851): :\det(A)(\det(A^u_v))^=\det(\tilde^u_v). When ''m'' =& ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix (mathematics)
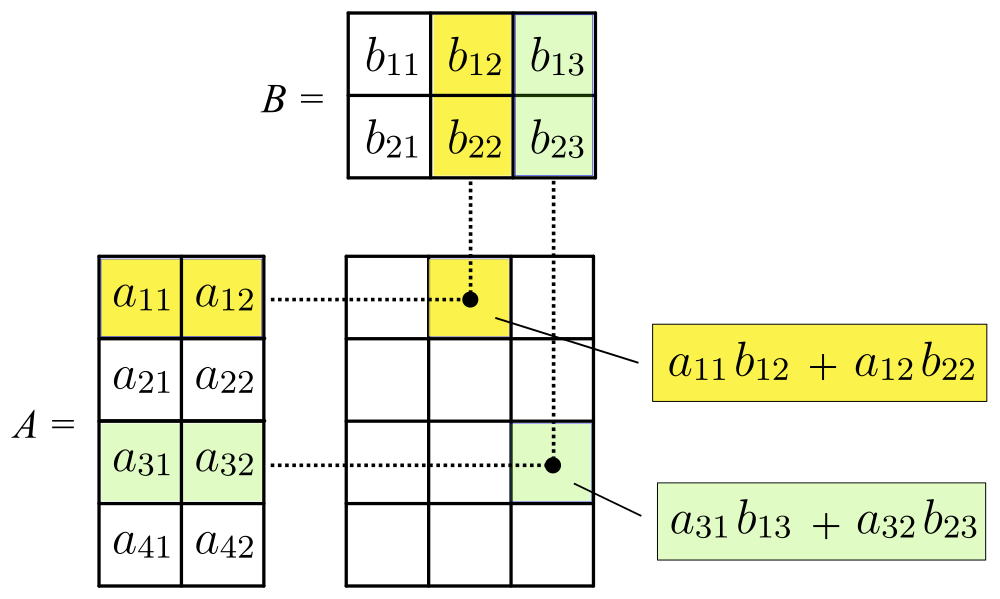
In mathematics, a matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two by three matrix", a "-matrix", or a matrix of dimension . Without further specifications, matrices represent linear maps, and allow explicit computations in linear algebra. Therefore, the study of matrices is a large part of linear algebra, and most properties and operations of abstract linear algebra can be expressed in terms of matrices. For example, matrix multiplication represents composition of linear maps. Not all matrices are related to linear algebra. This is, in particular, the case in graph theory, of incidence matrices, and adjacency matrices. ''This article focuses on matrices related to linear algebra, and, unle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Identity (mathematics)
In mathematics, an identity is an equality relating one mathematical expression ''A'' to another mathematical expression ''B'', such that ''A'' and ''B'' (which might contain some variables) produce the same value for all values of the variables within a certain range of validity. In other words, ''A'' = ''B'' is an identity if ''A'' and ''B'' define the same functions, and an identity is an equality between functions that are differently defined. For example, (a+b)^2 = a^2 + 2ab + b^2 and \cos^2\theta + \sin^2\theta =1 are identities. Identities are sometimes indicated by the triple bar symbol instead of , the equals sign. Common identities Algebraic identities Certain identities, such as a+0=a and a+(-a)=0, form the basis of algebra, while other identities, such as (a+b)^2 = a^2 + 2ab +b^2 and a^2 - b^2 = (a+b)(a-b), can be useful in simplifying algebraic expressions and expanding them. Trigonometric identities Geometrically, trigonometric ide ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Determinant
In mathematics, the determinant is a scalar value that is a function of the entries of a square matrix. It characterizes some properties of the matrix and the linear map represented by the matrix. In particular, the determinant is nonzero if and only if the matrix is invertible and the linear map represented by the matrix is an isomorphism. The determinant of a product of matrices is the product of their determinants (the preceding property is a corollary of this one). The determinant of a matrix is denoted , , or . The determinant of a matrix is :\begin a & b\\c & d \end=ad-bc, and the determinant of a matrix is : \begin a & b & c \\ d & e & f \\ g & h & i \end= aei + bfg + cdh - ceg - bdi - afh. The determinant of a matrix can be defined in several equivalent ways. Leibniz formula expresses the determinant as a sum of signed products of matrix entries such that each summand is the product of different entries, and the number of these summands is n!, the factorial of (t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
James Joseph Sylvester
James Joseph Sylvester (3 September 1814 – 15 March 1897) was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory, and combinatorics. He played a leadership role in American mathematics in the later half of the 19th century as a professor at the Johns Hopkins University and as founder of the ''American Journal of Mathematics''. At his death, he was a professor at Oxford University. Biography James Joseph was born in London on 3 September 1814, the son of Abraham Joseph, a Jewish merchant. James later adopted the surname Sylvester when his older brother did so upon emigration to the United States—a country which at that time required all immigrants to have a given name, a middle name, and a surname. At the age of 14, Sylvester was a student of Augustus de Morgan at the University of London. His family withdrew him from the University after he was accused of stabbing a fellow student with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subset
In mathematics, Set (mathematics), set ''A'' is a subset of a set ''B'' if all Element (mathematics), elements of ''A'' are also elements of ''B''; ''B'' is then a superset of ''A''. It is possible for ''A'' and ''B'' to be equal; if they are unequal, then ''A'' is a proper subset of ''B''. The relationship of one set being a subset of another is called inclusion (or sometimes containment). ''A'' is a subset of ''B'' may also be expressed as ''B'' includes (or contains) ''A'' or ''A'' is included (or contained) in ''B''. A ''k''-subset is a subset with ''k'' elements. The subset relation defines a partial order on sets. In fact, the subsets of a given set form a Boolean algebra (structure), Boolean algebra under the subset relation, in which the join and meet are given by Intersection (set theory), intersection and Union (set theory), union, and the subset relation itself is the Inclusion (Boolean algebra), Boolean inclusion relation. Definition If ''A'' and ''B'' are sets and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Desnanot-jacobi Identity
In mathematics, Dodgson condensation or method of contractants is a method of computing the determinants of square matrices. It is named for its inventor, Charles Lutwidge Dodgson (better known by his pseudonym, as Lewis Carroll, the popular author). The method in the case of an ''n'' × ''n'' matrix is to construct an (''n'' − 1) × (''n'' − 1) matrix, an (''n'' − 2) × (''n'' − 2), and so on, finishing with a 1 × 1 matrix, which has one entry, the determinant of the original matrix. General method This algorithm can be described in the following four steps: # Let A be the given ''n'' × ''n'' matrix. Arrange A so that no zeros occur in its interior. An explicit definition of interior would be all ai,j with i,j\ne1,n. One can do this using any operation that one could normally perform without changing the value of the determinant, such as adding a multiple of one row to another. # Cr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weinstein–Aronszajn Identity
In mathematics, the Weinstein–Aronszajn identity states that if A and B are matrices of size and respectively (either or both of which may be infinite) then, provided AB (and hence, also BA) is of trace class, :\det(I_m + AB) = \det(I_n + BA), where I_k is the identity matrix. It is closely related to the matrix determinant lemma and its generalization. It is the determinant analogue of the Woodbury matrix identity for matrix inverses. Proof The identity may be proved as follows. Let M be a matrix comprising the four blocks I_m, -A, B and I_n. :M = \begin I_m & -A \\ B & I_n \end. Because is invertible, the formula for the determinant of a block matrix gives :\det\begin I_m & -A \\ B & I_n \end = \det(I_m) \det\left(I_n - B I_m^ (-A)\right) = \det(I_n + BA). Because is invertible, the formula for the determinant of a block matrix gives :\det\begin I_m & -A\\ B & I_n \end = \det(I_n) \det\left(I_m - (-A) I_n^ B\right) = \det(I_m + AB). Thus :\det(I_n + B A) = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Determinants
In mathematics, the determinant is a scalar value that is a function of the entries of a square matrix. It characterizes some properties of the matrix and the linear map represented by the matrix. In particular, the determinant is nonzero if and only if the matrix is invertible and the linear map represented by the matrix is an isomorphism. The determinant of a product of matrices is the product of their determinants (the preceding property is a corollary of this one). The determinant of a matrix is denoted , , or . The determinant of a matrix is :\begin a & b\\c & d \end=ad-bc, and the determinant of a matrix is : \begin a & b & c \\ d & e & f \\ g & h & i \end= aei + bfg + cdh - ceg - bdi - afh. The determinant of a matrix can be defined in several equivalent ways. Leibniz formula expresses the determinant as a sum of signed products of matrix entries such that each summand is the product of different entries, and the number of these summands is n!, the factorial of (the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Theory
In mathematics, a matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two by three matrix", a "-matrix", or a matrix of dimension . Without further specifications, matrices represent linear maps, and allow explicit computations in linear algebra. Therefore, the study of matrices is a large part of linear algebra, and most properties and operations of abstract linear algebra can be expressed in terms of matrices. For example, matrix multiplication represents composition of linear maps. Not all matrices are related to linear algebra. This is, in particular, the case in graph theory, of incidence matrices, and adjacency matrices. ''This article focuses on matrices related to linear algebra, and, un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |