|
Surface States
Surface states are electronic states found at the surface of materials. They are formed due to the sharp transition from solid material that ends with a surface and are found only at the atom layers closest to the surface. The termination of a material with a surface leads to a change of the electronic band structure from the bulk material to the vacuum. In the weakened potential at the surface, new electronic states can be formed, so called surface states. Origin at condensed matter interfaces As stated by Bloch's theorem, eigenstates of the single-electron Schrödinger equation with a perfectly periodic potential, a crystal, are Bloch waves : \begin \Psi_ &=\mathrm^u_(\boldsymbol). \end Here u_(\boldsymbol) is a function with the same periodicity as the crystal, ''n'' is the band index and k is the wave number. The allowed wave numbers for a given potential are found by applying the usual Born–von Karman cyclic boundary conditions. The termination of a crystal, i.e. the f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electronic State
A quantum mechanical system or particle that is bound—that is, confined spatially—can only take on certain discrete values of energy, called energy levels. This contrasts with classical particles, which can have any amount of energy. The term is commonly used for the energy levels of the electrons in atoms, ions, or molecules, which are bound by the electric field of the nucleus, but can also refer to energy levels of nuclei or vibrational or rotational energy levels in molecules. The energy spectrum of a system with such discrete energy levels is said to be quantized. In chemistry and atomic physics, an electron shell, or principal energy level, may be thought of as the orbit of one or more electrons around an atom's nucleus. The closest shell to the nucleus is called the " shell" (also called "K shell"), followed by the " shell" (or "L shell"), then the " shell" (or "M shell"), and so on farther and farther from the nucleus. The shells correspond with the principal quant ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Igor Tamm
Igor Yevgenyevich Tamm ( rus, И́горь Евге́ньевич Тамм , p=ˈiɡərʲ jɪvˈɡʲenʲjɪvitɕ ˈtam , a=Ru-Igor Yevgenyevich Tamm.ogg; 8 July 1895 – 12 April 1971) was a Soviet physicist who received the 1958 Nobel Prize in Physics, jointly with Pavel Alekseyevich Cherenkov and Ilya Mikhailovich Frank, for their 1934 discovery and demonstration of Cherenkov radiation. He also predicted the Quasi-particle Phonon, and in 1951, together with Andrei Sakharov were the proposers of the Tokamak system. Biography According to Russian sources, Tamm had German noble descent on his father's side through his grandfather Theodor Tamm, who emigrated from Thuringia. Although his surname "Tamm" is rather common in Estonia, other sources state he was Jewish or had Jewish ancestry. He studied at a gymnasium in Elisavetgrad (now Kropyvnytskyi, Ukraine). In 1913–1914 he studied at the University of Edinburgh together with his school-friend Boris Hessen. At the outbreak ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
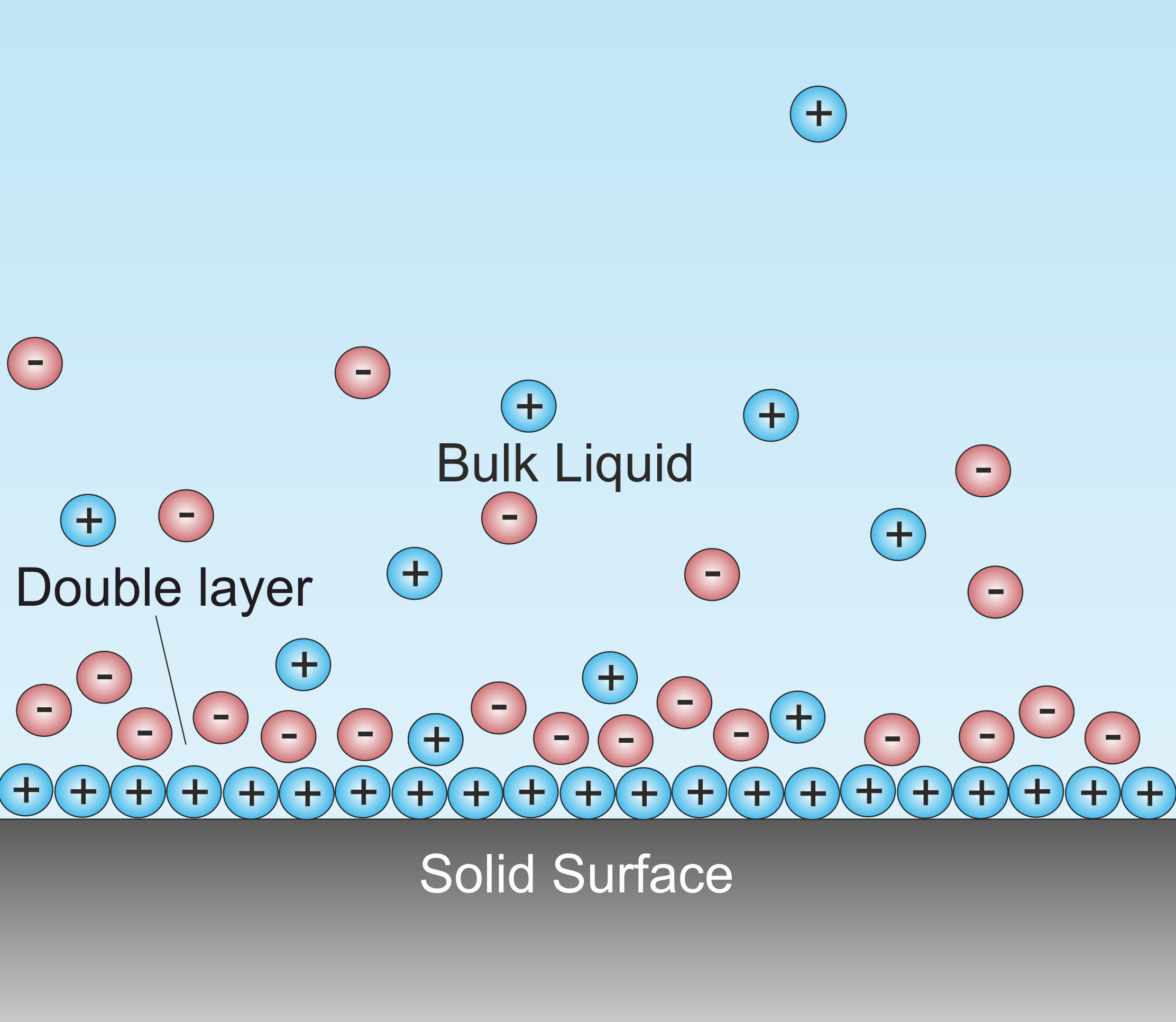
Double Layer (interfacial)
A double layer (DL, also called an electrical double layer, EDL) is a structure that appears on the surface of an object when it is exposed to a fluid. The object might be a solid particle, a gas bubble, a liquid droplet, or a porous body. The DL refers to two parallel layers of charge surrounding the object. The first layer, the surface charge (either positive or negative), consists of ions adsorbed onto the object due to chemical interactions. The second layer is composed of ions attracted to the surface charge via the Coulomb force, electrically screening the first layer. This second layer is loosely associated with the object. It is made of free ions that move in the fluid under the influence of electric attraction and thermal motion rather than being firmly anchored. It is thus called the "diffuse layer". Interfacial DLs are most apparent in systems with a large surface area to volume ratio, such as a colloid or porous bodies with particles or pores (respectively) on t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Charge Density
In electromagnetism, charge density is the amount of electric charge per unit length, surface area, or volume. Volume charge density (symbolized by the Greek letter ρ) is the quantity of charge per unit volume, measured in the SI system in coulombs per cubic meter (C⋅m−3), at any point in a volume. Surface charge density (σ) is the quantity of charge per unit area, measured in coulombs per square meter (C⋅m−2), at any point on a surface charge distribution on a two dimensional surface. Linear charge density (λ) is the quantity of charge per unit length, measured in coulombs per meter (C⋅m−1), at any point on a line charge distribution. Charge density can be either positive or negative, since electric charge can be either positive or negative. Like mass density, charge density can vary with position. In classical electromagnetic theory charge density is idealized as a ''continuous'' scalar function of position \boldsymbol, like a fluid, and \rho(\boldsymbol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Step Function
In mathematics, a function on the real numbers is called a step function if it can be written as a finite linear combination of indicator functions of intervals. Informally speaking, a step function is a piecewise constant function having only finitely many pieces. Definition and first consequences A function f\colon \mathbb \rightarrow \mathbb is called a step function if it can be written as :f(x) = \sum\limits_^n \alpha_i \chi_(x), for all real numbers x where n\ge 0, \alpha_i are real numbers, A_i are intervals, and \chi_A is the indicator function of A: :\chi_A(x) = \begin 1 & \text x \in A \\ 0 & \text x \notin A \\ \end In this definition, the intervals A_i can be assumed to have the following two properties: # The intervals are pairwise disjoint: A_i \cap A_j = \emptyset for i \neq j # The union of the intervals is the entire real line: \bigcup_^n A_i = \mathbb R. Indeed, if that is not the case to start with, a different set of intervals can be picked for whi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another. History Geometric topology as an area distinct from algebraic topology may be said to have originated in the 1935 classification of lens spaces by Reidemeister torsion, which required distinguishing spaces that are homotopy equivalent but not homeomorphic. This was the origin of ''simple'' homotopy theory. The use of the term geometric topology to describe these seems to have originated rather recently. Differences between low-dimensional and high-dimensional topology Manifolds differ radically in behavior in high and low dimension. High-dimensional topology refers to manifolds of dimension 5 and above, or in relative terms, embeddings in codimension 3 and above. Low-dimensional topology is concerned with questions in dimensions up to 4, or embeddings in codimension up to 2. Dimension 4 is special, in that in some respects (topologica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Genus (mathematics)
In mathematics, genus (plural genera) has a few different, but closely related, meanings. Intuitively, the genus is the number of "holes" of a surface. A sphere has genus 0, while a torus has genus 1. Topology Orientable surfaces The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It is equal to the number of handles on it. Alternatively, it can be defined in terms of the Euler characteristic ''χ'', via the relationship ''χ'' = 2 − 2''g'' for closed surfaces, where ''g'' is the genus. For surfaces with ''b'' boundary components, the equation reads ''χ'' = 2 − 2''g'' − ''b''. In layman's terms, it's the number of "holes" an object has ("holes" interpreted in the sense of doughnut holes; a hollow sphere would be considered as having zero holes in this sense). A torus has 1 such h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wide Gap Semiconductors
Wide-bandgap semiconductors (also known as WBG semiconductors or WBGSs) are semiconductor materials which have a larger band gap than conventional semiconductors. Conventional semiconductors like silicon have a bandgap in the range of 0.6 – 1.5 electronvolt (eV), whereas wide-bandgap materials have bandgaps in the range above 2 eV. Generally, wide-bandgap semiconductors have electronic properties which fall in between those of conventional semiconductors and insulator (electricity), insulators. Wide-bandgap semiconductors permit devices to operate at much higher voltages, frequencies, and temperatures than conventional semiconductor materials like silicon and gallium arsenide. They are the key component used to make short-wavelength (green-UV) light-emitting diode, LEDs or lasers, and are also used in certain radio frequency applications, notably military radars. Their intrinsic qualities make them suitable for a wide range of other applications, and they are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transition Metal
In chemistry, a transition metal (or transition element) is a chemical element in the d-block of the periodic table (groups 3 to 12), though the elements of group 12 (and less often group 3) are sometimes excluded. They are the elements that can use d orbitals as valence orbitals to form chemical bonds. The lanthanide and actinide elements (the f-block) are called inner transition metals and are sometimes considered to be transition metals as well. Since they are metals, they are lustrous and have good electrical and thermal conductivity. Most (with the exception of group 11 and group 12) are hard and strong, and have high melting and boiling temperatures. They form compounds in any of two or more different oxidation states and bind to a variety of ligands to form coordination complexes that are often coloured. They form many useful alloys and are often employed as catalysts in elemental form or in compounds such as coordination complexes and oxides. Most are strongly param ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Combinations Of Atomic Orbitals
A linear combination of atomic orbitals or LCAO is a quantum superposition of atomic orbitals and a technique for calculating molecular orbitals in quantum chemistry. In quantum mechanics, electron configurations of atoms are described as wavefunctions. In a mathematical sense, these wave functions are the basis set of functions, the basis functions, which describe the electrons of a given atom. In chemical reactions, orbital wavefunctions are modified, i.e. the electron cloud shape is changed, according to the type of atoms participating in the chemical bond. It was introduced in 1929 by Sir John Lennard-Jones with the description of bonding in the diatomic molecules of the first main row of the periodic table, but had been used earlier by Linus Pauling for H2+. Mathematical description An initial assumption is that the number of molecular orbitals is equal to the number of atomic orbitals included in the linear expansion. In a sense, ''n'' atomic orbitals combine to form '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Function
A wave function in quantum physics is a mathematical description of the quantum state of an isolated quantum system. The wave function is a complex-valued probability amplitude, and the probabilities for the possible results of measurements made on the system can be derived from it. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi, respectively). The wave function is a function of the degrees of freedom corresponding to some maximal set of commuting observables. Once such a representation is chosen, the wave function can be derived from the quantum state. For a given system, the choice of which commuting degrees of freedom to use is not unique, and correspondingly the domain of the wave function is also not unique. For instance, it may be taken to be a function of all the position coordinates of the particles over position space, or the momenta of all the particles over momentum space; the two are related by a Fourier tran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tight Binding
In solid-state physics, the tight-binding model (or TB model) is an approach to the calculation of electronic band structure using an approximate set of wave functions based upon superposition of wave functions for isolated atoms located at each atomic site. The method is closely related to the LCAO method (linear combination of atomic orbitals method) used in chemistry. Tight-binding models are applied to a wide variety of solids. The model gives good qualitative results in many cases and can be combined with other models that give better results where the tight-binding model fails. Though the tight-binding model is a one-electron model, the model also provides a basis for more advanced calculations like the calculation of surface states and application to various kinds of many-body problem and quasiparticle calculations. Introduction The name "tight binding" of this electronic band structure model suggests that this quantum mechanical model describes the properties of tightly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |