|
Stuart Samuel (physicist)
Stuart Samuel is a theoretical physicist known for his work on the speed of gravity and for his work with Alan Kostelecký on spontaneous Lorentz violation in string theory, now called the Bumblebee model. He also made significant contributions in field theory and particle physics. Samuel graduated from Princeton University with a Bachelor of Arts in mathematics in 1975, and in 1979, he graduated from the UC Berkeley, with a Doctor of Philosophy in physics. He was formerly a member of the Institute for Advanced Study at Princeton, a professor of physics at Columbia University, and a professor of physics at City College of New York. Earlier work In early work, Samuel used particle field theory methods to obtain results in statistical mechanics. In particular, Samuel uncovered a particularly simple way to solve the two-dimensional Ising model. It was shown to be equivalent to a non-interacting field theory of fermionic-like particles. This allowed a rapid computatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theoretical Physics
Theoretical physics is a branch of physics that employs mathematical models and abstractions of physical objects and systems to rationalize, explain and predict natural phenomena. This is in contrast to experimental physics, which uses experimental tools to probe these phenomena. The advancement of science generally depends on the interplay between experimental studies and theory. In some cases, theoretical physics adheres to standards of mathematical rigour while giving little weight to experiments and observations.There is some debate as to whether or not theoretical physics uses mathematics to build intuition and illustrativeness to extract physical insight (especially when normal experience fails), rather than as a tool in formalizing theories. This links to the question of it using mathematics in a less formally rigorous, and more intuitive or heuristic way than, say, mathematical physics. For example, while developing special relativity, Albert Einstein was concerned wit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partition Function (statistical Mechanics)
In physics, a partition function describes the statistical properties of a system in thermodynamic equilibrium. Partition functions are functions of the thermodynamic state variables, such as the temperature and volume. Most of the aggregate thermodynamic variables of the system, such as the total energy, free energy, entropy, and pressure, can be expressed in terms of the partition function or its derivatives. The partition function is dimensionless. Each partition function is constructed to represent a particular statistical ensemble (which, in turn, corresponds to a particular free energy). The most common statistical ensembles have named partition functions. The canonical partition function applies to a canonical ensemble, in which the system is allowed to exchange heat with the environment at fixed temperature, volume, and number of particles. The grand canonical partition function applies to a grand canonical ensemble, in which the system can exchange both heat and p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spontaneous Symmetry Breaking
Spontaneous symmetry breaking is a spontaneous process of symmetry breaking, by which a physical system in a symmetric state spontaneously ends up in an asymmetric state. In particular, it can describe systems where the equations of motion or the Lagrangian obey symmetries, but the lowest-energy vacuum solutions do not exhibit that same symmetry. When the system goes to one of those vacuum solutions, the symmetry is broken for perturbations around that vacuum even though the entire Lagrangian retains that symmetry. Overview By definition, spontaneous symmetry breaking requires the existence of physical laws (e.g. quantum mechanics) which are invariant under a symmetry transformation (such as translation or rotation), so that any pair of outcomes differing only by that transformation have the same probability distribution. For example if measurements of an observable at any two different positions have the same probability distribution, the observable has translational symmetry. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pion
In particle physics, a pion (or a pi meson, denoted with the Greek letter pi: ) is any of three subatomic particles: , , and . Each pion consists of a quark and an antiquark and is therefore a meson. Pions are the lightest mesons and, more generally, the lightest hadrons. They are unstable, with the charged pions and decaying after a mean lifetime of 26.033 nanoseconds ( seconds), and the neutral pion decaying after a much shorter lifetime of 85 attoseconds ( seconds). Charged pions most often decay into muons and muon neutrinos, while neutral pions generally decay into gamma rays. The exchange of virtual pions, along with vector, rho and omega mesons, provides an explanation for the residual strong force between nucleons. Pions are not produced in radioactive decay, but commonly are in high-energy collisions between hadrons. Pions also result from some matter–antimatter annihilation events. All types of pions are also produced in natural processes wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Meson
In particle physics, a meson ( or ) is a type of hadronic subatomic particle composed of an equal number of quarks and antiquarks, usually one of each, bound together by the strong interaction. Because mesons are composed of quark subparticles, they have a meaningful physical size, a diameter of roughly one femtometre (10 m), which is about 0.6 times the size of a proton or neutron. All mesons are unstable, with the longest-lived lasting for only a few hundredths of a microsecond. Heavier mesons decay to lighter mesons and ultimately to stable electrons, neutrinos and photons. Outside the nucleus, mesons appear in nature only as short-lived products of very high-energy collisions between particles made of quarks, such as cosmic rays (high-energy protons and neutrons) and baryonic matter. Mesons are routinely produced artificially in cyclotrons or other particle accelerators in the collisions of protons, antiprotons, or other particles. Higher-energy (more massive) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermion Doubling
In lattice field theory, fermion doubling occurs when naively putting fermionic fields on a lattice, resulting in more fermionic states than expected. For the naively discretized Dirac fermions in d Euclidean dimensions, each fermionic field results in 2^d identical fermion species, referred to as different tastes of the fermion. The fermion doubling problem is intractably linked to chiral invariance by the Nielsen–Ninomiya theorem. Most strategies used to solve the problem require using modified fermions which reduce to the Dirac fermion only in the continuum limit. Naive fermion discretization For simplicity we will consider a four-dimensional theory of a free fermion, although the fermion doubling problem remains in arbitrary dimensions and even if interactions are included. Lattice field theory is usually carried out in Euclidean spacetime arrived at from Minkowski spacetime after a Wick rotation, where the continuum Dirac action takes the form : S_F psi, \bar \psi= \in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
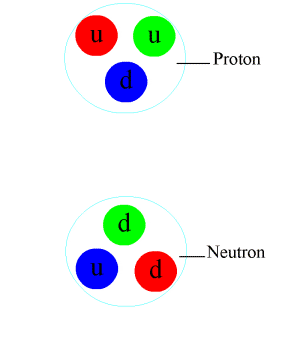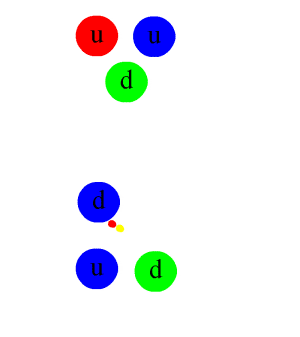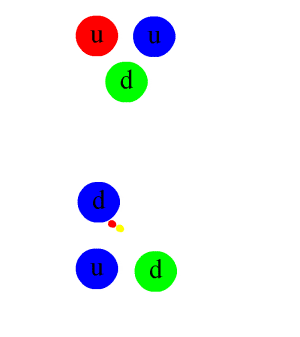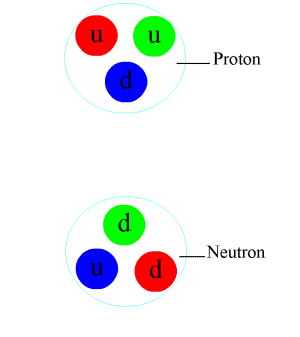
Quark
A quark () is a type of elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. All commonly observable matter is composed of up quarks, down quarks and electrons. Owing to a phenomenon known as ''color confinement'', quarks are never found in isolation; they can be found only within hadrons, which include baryons (such as protons and neutrons) and mesons, or in quark–gluon plasmas. There is also the theoretical possibility of more exotic phases of quark matter. For this reason, much of what is known about quarks has been drawn from observations of hadrons. Quarks have various intrinsic properties, including electric charge, mass, color charge, and spin. They are the only elementary particles in the Standard Model of particle physics to experience all four fundamental interactions, also known as ''fundamental forces'' (electro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scalar Field Theory
In theoretical physics, scalar field theory can refer to a relativistically invariant classical or quantum theory of scalar fields. A scalar field is invariant under any Lorentz transformation. The only fundamental scalar quantum field that has been observed in nature is the Higgs field. However, scalar quantum fields feature in the effective field theory descriptions of many physical phenomena. An example is the pion, which is actually a pseudoscalar. Since they do not involve polarization complications, scalar fields are often the easiest to appreciate second quantization through. For this reason, scalar field theories are often used for purposes of introduction of novel concepts and techniques. The signature of the metric employed below is . Classical scalar field theory A general reference for this section is Ramond, Pierre (2001-12-21). Field Theory: A Modern Primer (Second Edition). USA: Westview Press. , Ch 1. Linear (free) theory The most basic scalar field theo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perturbation Theory
In mathematics and applied mathematics, perturbation theory comprises methods for finding an approximate solution to a problem, by starting from the exact solution of a related, simpler problem. A critical feature of the technique is a middle step that breaks the problem into "solvable" and "perturbative" parts. In perturbation theory, the solution is expressed as a power series in a small parameter The first term is the known solution to the solvable problem. Successive terms in the series at higher powers of \varepsilon usually become smaller. An approximate 'perturbation solution' is obtained by truncating the series, usually by keeping only the first two terms, the solution to the known problem and the 'first order' perturbation correction. Perturbation theory is used in a wide range of fields, and reaches its most sophisticated and advanced forms in quantum field theory. Perturbation theory (quantum mechanics) describes the use of this method in quantum mechanics. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermion
In particle physics, a fermion is a particle that follows Fermi–Dirac statistics. Generally, it has a half-odd-integer spin: spin , spin , etc. In addition, these particles obey the Pauli exclusion principle. Fermions include all quarks and leptons and all composite particles made of an odd number of these, such as all baryons and many atoms and nuclei. Fermions differ from bosons, which obey Bose–Einstein statistics. Some fermions are elementary particles (such as electrons), and some are composite particles (such as protons). For example, according to the spin-statistics theorem in relativistic quantum field theory, particles with integer spin are bosons. In contrast, particles with half-integer spin are fermions. In addition to the spin characteristic, fermions have another specific property: they possess conserved baryon or lepton quantum numbers. Therefore, what is usually referred to as the spin-statistics relation is, in fact, a spin statistics-quantum numb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.png)