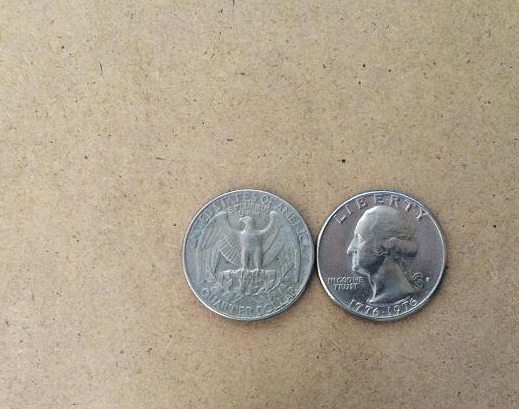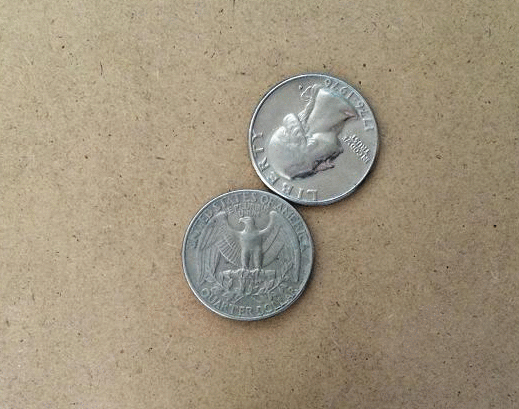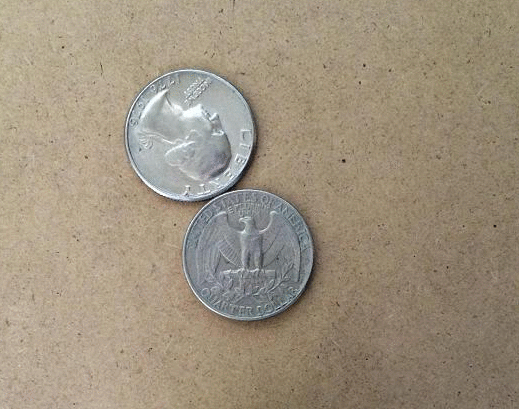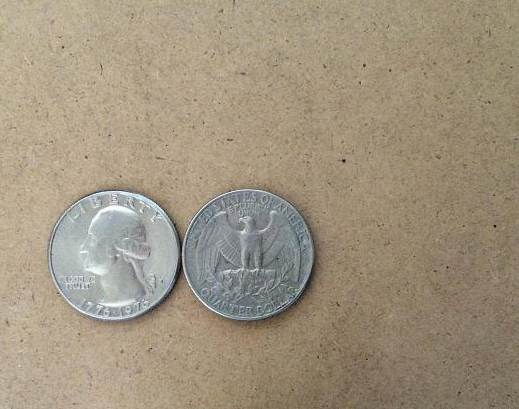|
String Girdling Earth
String girdling Earth is a mathematical puzzle with a counterintuitive solution. In a version of this puzzle, string is tightly wrapped around the equator of a perfectly spherical Earth. If the string should be raised off the ground, all the way along the equator, how much longer would the string be? Alternatively, of string is spliced into the original string, and the extended string rearranged so that it is at a uniform height above the equator. The question that is then posed is whether the gap between string and Earth will allow the passage of a car, a cat or a thin knife blade. Solution As the string must be raised all along the entire circumference, one might expect several kilometres of additional string. Surprisingly, the answer is 2 or around . In the second phrasing, considering that is almost negligible compared with the circumference, the first response may be that the new position of the string will be no different from the original surface-hugging position. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
String Girdling Earth
String girdling Earth is a mathematical puzzle with a counterintuitive solution. In a version of this puzzle, string is tightly wrapped around the equator of a perfectly spherical Earth. If the string should be raised off the ground, all the way along the equator, how much longer would the string be? Alternatively, of string is spliced into the original string, and the extended string rearranged so that it is at a uniform height above the equator. The question that is then posed is whether the gap between string and Earth will allow the passage of a car, a cat or a thin knife blade. Solution As the string must be raised all along the entire circumference, one might expect several kilometres of additional string. Surprisingly, the answer is 2 or around . In the second phrasing, considering that is almost negligible compared with the circumference, the first response may be that the new position of the string will be no different from the original surface-hugging position. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Counterintuitive
A paradox is a logically self-contradictory statement or a statement that runs contrary to one's expectation. It is a statement that, despite apparently valid reasoning from true premises, leads to a seemingly self-contradictory or a logically unacceptable conclusion. A paradox usually involves contradictory-yet-interrelated elements that exist simultaneously and persist over time. They result in "persistent contradiction between interdependent elements" leading to a lasting "unity of opposites". In logic, many paradoxes exist that are known to be invalid arguments, yet are nevertheless valuable in promoting critical thinking, while other paradoxes have revealed errors in definitions that were assumed to be rigorous, and have caused axioms of mathematics and logic to be re-examined. One example is Russell's paradox, which questions whether a "list of all lists that do not contain themselves" would include itself, and showed that attempts to found set theory on the identification ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
String Girdling Square
String or strings may refer to: * String (structure), a long flexible structure made from threads twisted together, which is used to tie, bind, or hang other objects Arts, entertainment, and media Films * ''Strings'' (1991 film), a Canadian animated short * ''Strings'' (2004 film), a film directed by Anders Rønnow Klarlund * ''Strings'' (2011 film), an American dramatic thriller film * ''Strings'' (2012 film), a British film by Rob Savage * ''Bravetown'' (2015 film), an American drama film originally titled ''Strings'' * ''The String'' (2009), a French film Music Instruments * String (music), the flexible element that produces vibrations and sound in string instruments * String instrument, a musical instrument that produces sound through vibrating strings ** List of string instruments * String piano, a pianistic extended technique in which sound is produced by direct manipulation of the strings, rather than striking the piano's keys Types of groups * String band, musical e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Milky Way
The Milky Way is the galaxy that includes our Solar System, with the name describing the galaxy's appearance from Earth: a hazy band of light seen in the night sky formed from stars that cannot be individually distinguished by the naked eye. The term ''Milky Way'' is a translation of the Latin ', from the Greek ('), meaning "milky circle". From Earth, the Milky Way appears as a band because its disk-shaped structure is viewed from within. Galileo Galilei first resolved the band of light into individual stars with his telescope in 1610. Until the early 1920s, most astronomers thought that the Milky Way contained all the stars in the Universe. Following the 1920 Great Debate between the astronomers Harlow Shapley and Heber Curtis, observations by Edwin Hubble showed that the Milky Way is just one of many galaxies. The Milky Way is a barred spiral galaxy with an estimated D25 isophotal diameter of , but only about 1,000 light years thick at the spiral arms (more at the bulg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coin Rotation Paradox
The coin rotation paradox is the counter-intuitive observation that, when one coin is rolled around the rim of another coin of equal size, the moving coin completes two full rotations after going all the way around the stationary coin. Description Start with two identical coins touching each other on a table, with their "head" sides displayed and parallel. Keeping coin A stationary, rotate coin B around A, keeping a point of contact with no slippage. As coin B reaches the opposite side, the two heads will again be parallel; B has made one revolution. Continuing to move B brings it back to the starting position and completes a second revolution. Paradoxically, coin B appears to have rolled a distance equal to twice its circumference. In reality, as the circumferences of both coins are equal, by definition coin B has only rolled a distance equal to its own circumference. The second rotation arises from the fact that the path along which it has rolled is a circle. This is analogous ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simple Polygon
In geometry, a simple polygon is a polygon that does not Intersection (Euclidean geometry), intersect itself and has no holes. That is, it is a flat shape consisting of straight, non-intersecting line segments or "sides" that are joined pairwise to form a single closed curve, closed path. If the sides intersect then the polygon is not simple. The qualifier "simple" is frequently omitted, with the above definition then being understood to define a polygon in general. The definition given above ensures the following properties: * A polygon encloses a region (mathematics), region (called its interior) which always has a measurable area. * The line segments that make up a polygon (called sides or edges) meet only at their endpoints, called vertices (singular: vertex) or less formally "corners". * Exactly two edges meet at each vertex. * The number of edges always equals the number of vertices. Two edges meeting at a corner are usually required to form an angle that is not straight ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Polygon
The term ''complex polygon'' can mean two different things: * In geometry, a polygon in the unitary plane, which has two complex dimensions. * In computer graphics, a polygon whose boundary is not simple. Geometry In geometry, a complex polygon is a polygon in the complex Hilbert plane, which has two complex dimensions. A complex number may be represented in the form (a + ib), where a and b are real numbers, and i is the square root of -1. Multiples of i such as ib are called ''imaginary numbers''. A complex number lies in a complex plane having one real and one imaginary dimension, which may be represented as an Argand diagram. So a single complex dimension comprises two spatial dimensions, but of different kinds - one real and the other imaginary. The unitary plane comprises two such complex planes, which are orthogonal to each other. Thus it has two real dimensions and two imaginary dimensions. A complex polygon is a (complex) two-dimensional (i.e. four spatial dimensions) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Winding Number
In mathematics, the winding number or winding index of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point, i.e., the curve's number of turns. The winding number depends on the orientation of the curve, and it is negative if the curve travels around the point clockwise. Winding numbers are fundamental objects of study in algebraic topology, and they play an important role in vector calculus, complex analysis, geometric topology, differential geometry, and physics (such as in string theory). Intuitive description Suppose we are given a closed, oriented curve in the ''xy'' plane. We can imagine the curve as the path of motion of some object, with the orientation indicating the direction in which the object moves. Then the winding number of the curve is equal to the total number of counterclockwise turns that the object makes around the origin. When counting the total nu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Visual Calculus
Visual calculus, invented by Mamikon Mnatsakanian (known as Mamikon), is an approach to solving a variety of integral calculus problems. Many problems that would otherwise seem quite difficult yield to the method with hardly a line of calculation, often reminiscent of what Martin Gardner called "aha! solutions" or Roger Nelsen a proof without words. Description Mamikon devised his method in 1959 while an undergraduate, first applying it to a well-known geometry problem: find the area of a ring (annulus), given the length of a chord tangent to the inner circumference. Perhaps surprisingly, no additional information is needed; the solution does not depend on the ring's inner and outer dimensions. The traditional approach involves algebra and application of the Pythagorean theorem. Mamikon's method, however, envisions an alternate construction of the ring: first the inner circle alone is drawn, then a constant-length tangent is made to travel along its circumference, "sweeping ou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Annulus (mathematics)
In mathematics, an annulus (plural annuli or annuluses) is the region between two concentric circles. Informally, it is shaped like a ring or a hardware washer. The word "annulus" is borrowed from the Latin word ''anulus'' or ''annulus'' meaning 'little ring'. The adjectival form is annular (as in annular eclipse). The open annulus is topologically equivalent to both the open cylinder and the punctured plane. Area The area of an annulus is the difference in the areas of the larger circle of radius and the smaller one of radius : :A = \pi R^2 - \pi r^2 = \pi\left(R^2 - r^2\right). The area of an annulus is determined by the length of the longest line segment within the annulus, which is the chord tangent to the inner circle, in the accompanying diagram. That can be shown using the Pythagorean theorem since this line is tangent to the smaller circle and perpendicular to its radius at that point, so and are sides of a right-angled triangle with hypotenuse , and the ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chord (geometry)
A chord of a circle is a straight line segment whose endpoints both lie on a circular arc. The infinite line extension of a chord is a secant line, or just ''secant''. More generally, a chord is a line segment joining two points on any curve, for instance, an ellipse. A chord that passes through a circle's center point is the circle's diameter. The word ''chord'' is from the Latin ''chorda'' meaning '' bowstring''. In circles Among properties of chords of a circle are the following: # Chords are equidistant from the center if and only if their lengths are equal. # Equal chords are subtended by equal angles from the center of the circle. # A chord that passes through the center of a circle is called a diameter and is the longest chord of that specific circle. # If the line extensions (secant lines) of chords AB and CD intersect at a point P, then their lengths satisfy AP·PB = CP·PD (power of a point theorem). In conics The midpoints of a set of parallel chords of a coni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Napkin Ring Problem
In geometry, the napkin-ring problem involves finding the volume of a "band" of specified height around a sphere, i.e. the part that remains after a hole in the shape of a circular cylinder is drilled through the center of the sphere. It is a counterintuitive fact that this volume does not depend on the original sphere's radius but only on the resulting band's height. The problem is so called because after removing a cylinder from the sphere, the remaining band resembles the shape of a napkin ring. Statement Suppose that the axis of a right circular cylinder passes through the center of a sphere of radius R and that h represents the height (defined as the distance in a direction parallel to the axis) of the part of the cylinder that is inside the sphere. The "band" is the part of the sphere that is outside the cylinder. The volume of the band depends on h but not on R: V=\frac. As the radius R of the sphere shrinks, the diameter of the cylinder must also shrink in order th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |