|
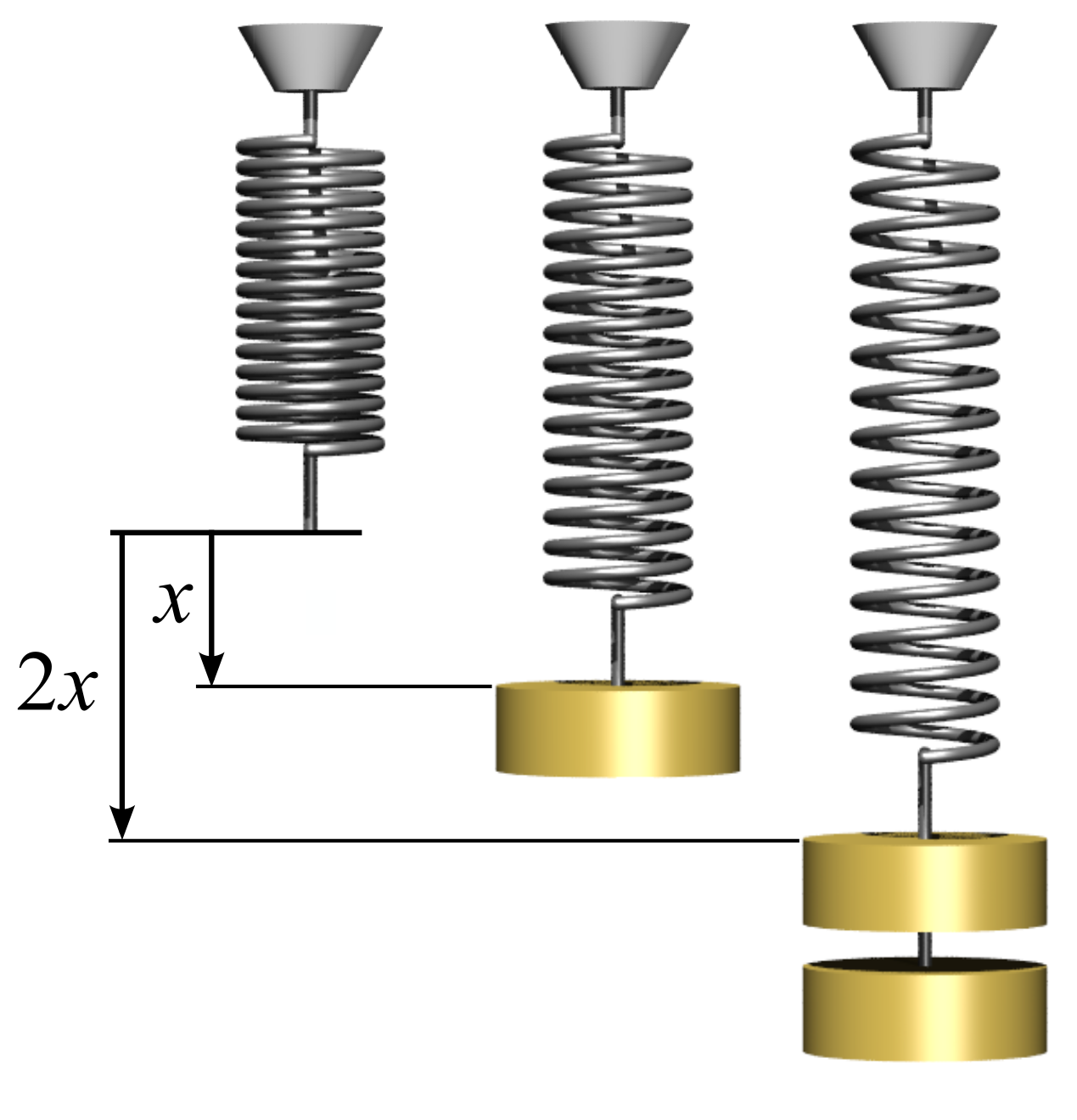
Stiffness
Stiffness is the extent to which an object resists deformation in response to an applied force. The complementary concept is flexibility or pliability: the more flexible an object is, the less stiff it is. Calculations The stiffness, k, of a body is a measure of the resistance offered by an elastic body to deformation. For an elastic body with a single degree of freedom (DOF) (for example, stretching or compression of a rod), the stiffness is defined as k = \frac where, * F is the force on the body * \delta is the displacement produced by the force along the same degree of freedom (for instance, the change in length of a stretched spring) In the International System of Units, stiffness is typically measured in newtons per meter (N/m). In Imperial units, stiffness is typically measured in pounds (lbs) per inch. Generally speaking, deflections (or motions) of an infinitesimal element (which is viewed as a point) in an elastic body can occur along multiple DOF (maximum of s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stiffness Of A Coil Spring
Stiffness is the extent to which an object resists deformation in response to an applied force. The complementary concept is flexibility or pliability: the more flexible an object is, the less stiff it is. Calculations The stiffness, k, of a body is a measure of the resistance offered by an elastic body to deformation. For an elastic body with a single degree of freedom (DOF) (for example, stretching or compression of a rod), the stiffness is defined as k = \frac where, * F is the force on the body * \delta is the displacement produced by the force along the same degree of freedom (for instance, the change in length of a stretched spring) In the International System of Units, stiffness is typically measured in newtons per meter (N/m). In Imperial units, stiffness is typically measured in pounds (lbs) per inch. Generally speaking, deflections (or motions) of an infinitesimal element (which is viewed as a point) in an elastic body can occur along multiple DOF (maximum of s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torsional Rigidity
Stiffness is the extent to which an object resists deformation in response to an applied force. The complementary concept is flexibility or pliability: the more flexible an object is, the less stiff it is. Calculations The stiffness, k, of a body is a measure of the resistance offered by an elastic body to deformation. For an elastic body with a single degree of freedom (DOF) (for example, stretching or compression of a rod), the stiffness is defined as k = \frac where, * F is the force on the body * \delta is the displacement produced by the force along the same degree of freedom (for instance, the change in length of a stretched spring) In the International System of Units, stiffness is typically measured in newtons per meter (N/m). In Imperial units, stiffness is typically measured in pounds (lbs) per inch. Generally speaking, deflections (or motions) of an infinitesimal element (which is viewed as a point) in an elastic body can occur along multiple DOF (maximum of six ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elasticity Tensor
In physics, Hooke's law is an empirical law which states that the force () needed to extend or compress a spring by some distance () scales linearly with respect to that distance—that is, where is a constant factor characteristic of the spring (i.e., its stiffness), and is small compared to the total possible deformation of the spring. The law is named after 17th-century British physicist Robert Hooke. He first stated the law in 1676 as a Latin anagram. He published the solution of his anagram in 1678 as: ("as the extension, so the force" or "the extension is proportional to the force"). Hooke states in the 1678 work that he was aware of the law since 1660. Hooke's equation holds (to some extent) in many other situations where an elastic body is deformed, such as wind blowing on a tall building, and a musician plucking a string of a guitar. An elastic body or material for which this equation can be assumed is said to be linear-elastic or Hookean. Hooke's law is on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Young's Modulus
Young's modulus E, the Young modulus, or the modulus of elasticity in tension or compression (i.e., negative tension), is a mechanical property that measures the tensile or compressive stiffness of a solid material when the force is applied lengthwise. It quantifies the relationship between tensile/compressive stress \sigma (force per unit area) and axial strain \varepsilon (proportional deformation) in the linear elastic region of a material and is determined using the formula: E = \frac Young's moduli are typically so large that they are expressed not in pascals but in gigapascals (GPa). Example: * Silly Putty (increasing pressure: length increases quickly, meaning tiny E) * Aluminum (increasing pressure: length increases slowly, meaning high E) Higher Young's modulus corresponds to greater (lengthwise) stiffness. Although Young's modulus is named after the 19th-century British scientist Thomas Young, the concept was developed in 1727 by Leonhard Euler. The first experime ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torsion Constant
The torsion constant is a geometrical property of a bar's cross-section which is involved in the relationship between angle of twist and applied torque along the axis of the bar, for a homogeneous linear-elastic bar. The torsion constant, together with material properties and length, describes a bar's torsional stiffness. The SI unit for torsion constant is m4. History In 1820, the French engineer A. Duleau derived analytically that the torsion constant of a beam is identical to the second moment of area normal to the section Jzz, which has an exact analytic equation, by assuming that a plane section before twisting remains planar after twisting, and a diameter remains a straight line. Unfortunately, that assumption is correct only in beams with circular cross-sections, and is incorrect for any other shape where warping takes place. For non-circular cross-sections, there are no exact analytical equations for finding the torsion constant. However, approximate solutions have been fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rigidity Modulus
In materials science, shear modulus or modulus of rigidity, denoted by ''G'', or sometimes ''S'' or ''μ'', is a measure of the elastic shear stiffness of a material and is defined as the ratio of shear stress to the shear strain: :G \ \stackrel\ \frac = \frac = \frac where :\tau_ = F/A \, = shear stress :F is the force which acts :A is the area on which the force acts :\gamma_ = shear strain. In engineering :=\Delta x/l = \tan \theta , elsewhere := \theta :\Delta x is the transverse displacement :l is the initial length of the area. The derived SI unit of shear modulus is the pascal (Pa), although it is usually expressed in gigapascals (GPa) or in thousand pounds per square inch (ksi). Its dimensional form is M1L−1T−2, replacing ''force'' by ''mass'' times ''acceleration''. Explanation The shear modulus is one of several quantities for measuring the stiffness of materials. All of them arise in the generalized Hooke's law: * Young's modulus ''E'' describes the mate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pascal (unit)
The pascal (symbol: Pa) is the unit of pressure in the International System of Units (SI), and is also used to quantify internal pressure, stress, Young's modulus, and ultimate tensile strength. The unit, named after Blaise Pascal, is defined as one newton per square metre and is equivalent to 10 barye (Ba) in the CGS system. The unit of measurement called standard atmosphere (atm) is defined as 101,325 Pa. Common multiple units of the pascal are the hectopascal (1 hPa = 100 Pa), which is equal to one millibar, and the kilopascal (1 kPa = 1000 Pa), which is equal to one centibar. Meteorological observations typically report atmospheric pressure in hectopascals per the recommendation of the World Meteorological Organization, thus a standard atmosphere (atm) or typical sea-level air pressure is about 1013 hPa. Reports in the United States typically use inches of mercury or millibars (hectopascals). In Canada these reports are given in kilopascal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elastic Modulus
An elastic modulus (also known as modulus of elasticity) is the unit of measurement of an object's or substance's resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it. The elastic modulus of an object is defined as the slope of its stress–strain curve in the elastic deformation region: A stiffer material will have a higher elastic modulus. An elastic modulus has the form: :\delta \ \stackrel\ \frac where stress is the force causing the deformation divided by the area to which the force is applied and strain is the ratio of the change in some parameter caused by the deformation to the original value of the parameter. Since strain is a dimensionless quantity, the units of \delta will be the same as the units of stress. Specifying how stress and strain are to be measured, including directions, allows for many types of elastic moduli to be defined. The three primary ones are: # ''Young's modulus'' (E) describes tensile and compressive ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deflection (engineering)
In structural engineering, deflection is the degree to which a part of a structural element is displaced under a load (because it deforms). It may refer to an angle or a distance. The deflection distance of a member under a load can be calculated by integrating the function that mathematically describes the slope of the deflected shape of the member under that load. Standard formulas exist for the deflection of common beam configurations and load cases at discrete locations. Otherwise methods such as virtual work, direct integration, Castigliano's method, Macaulay's method or the direct stiffness method are used. The deflection of beam elements is usually calculated on the basis of the Euler–Bernoulli beam equation while that of a plate or shell element is calculated using plate or shell theory. An example of the use of deflection in this context is in building construction. Architects and engineers select materials for various applications. [Baidu] |
Matrix (mathematics)
In mathematics, a matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two by three matrix", a "-matrix", or a matrix of dimension . Without further specifications, matrices represent linear maps, and allow explicit computations in linear algebra. Therefore, the study of matrices is a large part of linear algebra, and most properties and operations of abstract linear algebra can be expressed in terms of matrices. For example, matrix multiplication represents composition of linear maps. Not all matrices are related to linear algebra. This is, in particular, the case in graph theory, of incidence matrices, and adjacency matrices. ''This article focuses on matrices related to linear algebra, and, unle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intensive And Extensive Properties
Physical properties of materials and systems can often be categorized as being either intensive or extensive, according to how the property changes when the size (or extent) of the system changes. According to IUPAC, an intensive quantity is one whose magnitude is independent of the size of the system, whereas an extensive quantity is one whose magnitude is additive for subsystems. The terms ''intensive and extensive quantities'' were introduced into physics by German writer Georg Helm in 1898, and by American physicist and chemist Richard C. Tolman in 1917. An intensive property does not depend on the system size or the amount of material in the system. It is not necessarily homogeneously distributed in space; it can vary from place to place in a body of matter and radiation. Examples of intensive properties include temperature, ''T''; refractive index, ''n''; density, ''ρ''; and hardness, ''η''. By contrast, extensive properties such as the mass, volume and entropy of syst ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. The unit was formerly an SI supplementary unit (before that category was abolished in 1995). The radian is defined in the SI as being a dimensionless unit, with 1 rad = 1. Its symbol is accordingly often omitted, especially in mathematical writing. Definition One radian is defined as the angle subtended from the center of a circle which intercepts an arc equal in length to the radius of the circle. More generally, the magnitude in radians of a subtended angle is equal to the ratio of the arc length to the radius of the circle; that is, \theta = \frac, where is the subtended angle in radians, is arc length, and is radius. A right angle is exactly \frac radians. The rotation angle (360°) corresponding to one complete revolution is the length of the circumference divided by the radius, which i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |