|
Steiner Tree Problem
In combinatorial mathematics, the Steiner tree problem, or minimum Steiner tree problem, named after Jakob Steiner, is an umbrella term for a class of problems in combinatorial optimization. While Steiner tree problems may be formulated in a number of settings, they all require an optimal interconnect for a given set of objects and a predefined objective function. One well-known variant, which is often used synonymously with the term Steiner tree problem, is the Steiner tree problem in graphs. Given an undirected graph with non-negative edge weights and a subset of vertices, usually referred to as terminals, the Steiner tree problem in graphs requires a tree of minimum weight that contains all terminals (but may include additional vertices). Further well-known variants are the ''Euclidean Steiner tree problem'' and the '' rectilinear minimum Steiner tree problem''. The Steiner tree problem in graphs can be seen as a generalization of two other famous combinatorial optimization ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steiner 3 Points , the professional wrestling "tag team" of real-life brothers Rick and Scott Steiner
{{disambiguation, geo ...
Steiner may refer to: Felix Steiner, German Waffen SS-commander Surname *Steiner (surname) Other uses *Steiner, Michigan, a village in the United States * Steiner, Mississippi * Steiner Studios, film and television production studio in New York City * Steiner's theorem, used to determine the mass moment of inertia around an axis. Also known as parallel axis theorem See also * Poncelet–Steiner theorem *Steiner point (other) * Steiner surface *Steiner system, a type of block design *Steiner tree *Waldorf education, also called Steiner education *The Steiner Brothers The Steiner Brothers are an American professional wrestling tag team consisting of brothers Robert "Rick Steiner" Rechsteiner and Scott "Scott Steiner" Rechsteiner. The brothers wrestled as amateurs at the University of Michigan. The team ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electrical Network
An electrical network is an interconnection of electrical components (e.g., batteries, resistors, inductors, capacitors, switches, transistors) or a model of such an interconnection, consisting of electrical elements (e.g., voltage sources, current sources, resistances, inductances, capacitances). An electrical circuit is a network consisting of a closed loop, giving a return path for the current. Linear electrical networks, a special type consisting only of sources (voltage or current), linear lumped elements (resistors, capacitors, inductors), and linear distributed elements (transmission lines), have the property that signals are linearly superimposable. They are thus more easily analyzed, using powerful frequency domain methods such as Laplace transforms, to determine DC response, AC response, and transient response. A resistive circuit is a circuit containing only resistors and ideal current and voltage sources. Analysis of resistive circuits is less complicated t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optimization Problem
In mathematics, computer science and economics, an optimization problem is the problem of finding the ''best'' solution from all feasible solutions. Optimization problems can be divided into two categories, depending on whether the variables are continuous or discrete: * An optimization problem with discrete variables is known as a ''discrete optimization'', in which an object such as an integer, permutation or graph must be found from a countable set. * A problem with continuous variables is known as a ''continuous optimization'', in which an optimal value from a continuous function must be found. They can include constrained problems and multimodal problems. Continuous optimization problem The '' standard form'' of a continuous optimization problem is \begin &\underset& & f(x) \\ &\operatorname & &g_i(x) \leq 0, \quad i = 1,\dots,m \\ &&&h_j(x) = 0, \quad j = 1, \dots,p \end where * is the objective function to be minimized over the -variable vector , * are called ine ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
NP-hard
In computational complexity theory, NP-hardness ( non-deterministic polynomial-time hardness) is the defining property of a class of problems that are informally "at least as hard as the hardest problems in NP". A simple example of an NP-hard problem is the subset sum problem. A more precise specification is: a problem ''H'' is NP-hard when every problem ''L'' in NP can be reduced in polynomial time to ''H''; that is, assuming a solution for ''H'' takes 1 unit time, ''H''s solution can be used to solve ''L'' in polynomial time. As a consequence, finding a polynomial time algorithm to solve any NP-hard problem would give polynomial time algorithms for all the problems in NP. As it is suspected that P≠NP, it is unlikely that such an algorithm exists. It is suspected that there are no polynomial-time algorithms for NP-hard problems, but that has not been proven. Moreover, the class P, in which all problems can be solved in polynomial time, is contained in the NP class. Defi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
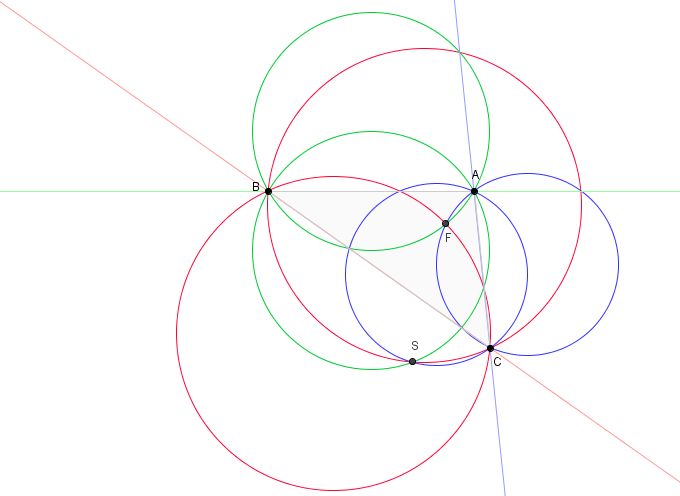
Fermat Point
In Euclidean geometry, the Fermat point of a triangle, also called the Torricelli point or Fermat–Torricelli point, is a point such that the sum of the three distances from each of the three vertices of the triangle to the point is the smallest possible. It is so named because this problem was first raised by Fermat in a private letter to Evangelista Torricelli, who solved it. The Fermat point gives a solution to the geometric median and Steiner tree problems for three points. Construction The Fermat point of a triangle with largest angle at most 120° is simply its first isogonic center or X(13), which is constructed as follows: # Construct an equilateral triangle on each of two arbitrarily chosen sides of the given triangle. # Draw a line from each new vertex to the opposite vertex of the original triangle. # The two lines intersect at the Fermat point. An alternative method is the following: # On each of two arbitrarily chosen sides, construct an isosceles triangle, with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree (graph Theory)
In graph theory, the degree (or valency) of a vertex of a graph is the number of edges that are incident to the vertex; in a multigraph, a loop contributes 2 to a vertex's degree, for the two ends of the edge. The degree of a vertex v is denoted \deg(v) or \deg v. The maximum degree of a graph G, denoted by \Delta(G), and the minimum degree of a graph, denoted by \delta(G), are the maximum and minimum of its vertices' degrees. In the multigraph shown on the right, the maximum degree is 5 and the minimum degree is 0. In a regular graph, every vertex has the same degree, and so we can speak of ''the'' degree of the graph. A complete graph (denoted K_n, where n is the number of vertices in the graph) is a special kind of regular graph where all vertices have the maximum possible degree, n-1. In a signed graph, the number of positive edges connected to the vertex v is called positive deg(v) and the number of connected negative edges is entitled negative deg(v). Handshaking lemma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steiner Point (computational Geometry)
In computational geometry, a Steiner point is a point that is not part of the input to a geometric optimization problem but is added during the solution of the problem, to create a better solution than would be possible from the original points alone. The name of these points comes from the Steiner tree problem, named after Jakob Steiner, in which the goal is to connect the input points by a network of minimum total length. If the input points alone are used as endpoints of the network edges, then the shortest network is their minimum spanning tree. However, shorter networks can often be obtained by adding Steiner points, and using both the new points and the input points as edge endpoints. Another problem that uses Steiner points is Steiner triangulation. The goal is to partition an input (such as a point set or polygon) into triangles, meeting edge-to-edge. Both input points and Steiner points may be used as triangle vertices. See also *Delaunay refinement In mesh generation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vojtěch Jarník
Vojtěch Jarník (; 1897–1970) was a Czech mathematician who worked for many years as a professor and administrator at Charles University, and helped found the Czechoslovak Academy of Sciences. He is the namesake of Jarník's algorithm for minimum spanning trees. Jarník worked in number theory, mathematical analysis, and graph algorithms. He has been called "probably the first Czechoslovak mathematician whose scientific works received wide and lasting international response". As well as developing Jarník's algorithm, he found tight bounds on the number of lattice points on convex curves, studied the relationship between the Hausdorff dimension of sets of real numbers and how well they can be approximated by rational numbers, and investigated the properties of nowhere-differentiable functions. Education and career Jarník was born December 22, 1897. He was the son of , a professor of Romance language philology at Charles University, and his older brother, Hertvík Jarník ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; german: Gauß ; la, Carolus Fridericus Gauss; 30 April 177723 February 1855) was a German mathematician and physicist who made significant contributions to many fields in mathematics and science. Sometimes referred to as the ''Princeps mathematicorum'' () and "the greatest mathematician since antiquity", Gauss had an exceptional influence in many fields of mathematics and science, and he is ranked among history's most influential mathematicians. Also available at Retrieved 23 February 2014. Comprehensive biographical article. Biography Early years Johann Carl Friedrich Gauss was born on 30 April 1777 in Brunswick (Braunschweig), in the Duchy of Brunswick-Wolfenbüttel (now part of Lower Saxony, Germany), to poor, working-class parents. His mother was illiterate and never recorded the date of his birth, remembering only that he had been born on a Wednesday, eight days before the Feast of the Ascension (which occurs 39 days after Easter). Ga ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Star (graph Theory)
In graph theory, a star is the complete bipartite graph a tree with one internal node and leaves (but no internal nodes and leaves when ). Alternatively, some authors define to be the tree of order with maximum diameter 2; in which case a star of has leaves. A star with 3 edges is called a claw. The star is edge-graceful when is even and not when is odd. It is an edge-transitive matchstick graph, and has diameter 2 (when ), girth ∞ (it has no cycles), chromatic index , and chromatic number 2 (when ). Additionally, the star has large automorphism group, namely, the symmetric group on letters. Stars may also be described as the only connected graphs in which at most one vertex has degree greater than one. Relation to other graph families Claws are notable in the definition of claw-free graphs, graphs that do not have any claw as an induced subgraph. They are also one of the exceptional cases of the Whitney graph isomorphism theorem: in general, graphs with isomor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Point (geometry)
In classical Euclidean geometry, a point is a primitive notion that models an exact location in space, and has no length, width, or thickness. In modern mathematics, a point refers more generally to an element of some set called a space. Being a primitive notion means that a point cannot be defined in terms of previously defined objects. That is, a point is defined only by some properties, called axioms, that it must satisfy; for example, ''"there is exactly one line that passes through two different points"''. Points in Euclidean geometry Points, considered within the framework of Euclidean geometry, are one of the most fundamental objects. Euclid originally defined the point as "that which has no part". In two-dimensional Euclidean space, a point is represented by an ordered pair (, ) of numbers, where the first number conventionally represents the horizontal and is often denoted by , and the second number conventionally represents the vertical and is often denoted by . ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line Segment
In geometry, a line segment is a part of a straight line that is bounded by two distinct end points, and contains every point on the line that is between its endpoints. The length of a line segment is given by the Euclidean distance between its endpoints. A closed line segment includes both endpoints, while an open line segment excludes both endpoints; a half-open line segment includes exactly one of the endpoints. In geometry, a line segment is often denoted using a line above the symbols for the two endpoints (such as \overline). Examples of line segments include the sides of a triangle or square. More generally, when both of the segment's end points are vertices of a polygon or polyhedron, the line segment is either an edge (geometry), edge (of that polygon or polyhedron) if they are adjacent vertices, or a diagonal. When the end points both lie on a curve (such as a circle), a line segment is called a chord (geometry), chord (of that curve). In real or complex vector spa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |