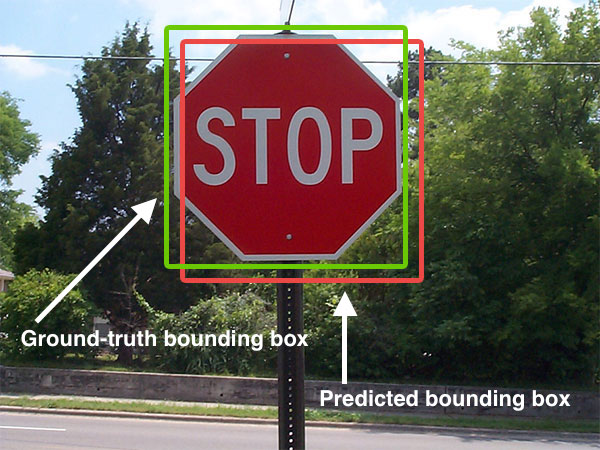
|
Speeded Up Robust Features
In computer vision, speeded up robust features (SURF) is a local feature detector and descriptor, with patented applications. It can be used for tasks such as object recognition, image registration, classification, or 3D reconstruction. It is partly inspired by the scale-invariant feature transform (SIFT) descriptor. The standard version of SURF is several times faster than SIFT and claimed by its authors to be more robust against different image transformations than SIFT. To detect interest points, SURF uses an integer approximation of the determinant of Hessian blob detector, which can be computed with 3 integer operations using a precomputed integral image. Its feature descriptor is based on the sum of the Haar wavelet response around the point of interest. These can also be computed with the aid of the integral image. SURF descriptors have been used to locate and recognize objects, people or faces, to reconstruct 3D scenes, to track objects and to extract points of int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Vision
Computer vision tasks include methods for image sensor, acquiring, Image processing, processing, Image analysis, analyzing, and understanding digital images, and extraction of high-dimensional data from the real world in order to produce numerical or symbolic information, e.g. in the form of decisions. "Understanding" in this context signifies the transformation of visual images (the input to the retina) into descriptions of the world that make sense to thought processes and can elicit appropriate action. This image understanding can be seen as the disentangling of symbolic information from image data using models constructed with the aid of geometry, physics, statistics, and learning theory. The scientific discipline of computer vision is concerned with the theory behind artificial systems that extract information from images. Image data can take many forms, such as video sequences, views from multiple cameras, multi-dimensional data from a 3D scanning, 3D scanner, 3D point clouds ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplacian Pyramid
Pyramid, or pyramid representation, is a type of multi-scale signal representation developed by the computer vision, image processing and signal processing communities, in which a signal or an image is subject to repeated smoothing and subsampling. Pyramid representation is a predecessor to scale-space representation and multiresolution analysis. Pyramid generation There are two main types of pyramids: lowpass and bandpass. A lowpass pyramid is made by smoothing the image with an appropriate smoothing filter and then subsampling the smoothed image, usually by a factor of 2 along each coordinate direction. The resulting image is then subjected to the same procedure, and the cycle is repeated multiple times. Each cycle of this process results in a smaller image with increased smoothing, but with decreased spatial sampling density (that is, decreased image resolution). If illustrated graphically, the entire multi-scale representation will look like a pyramid, with the original ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |