|
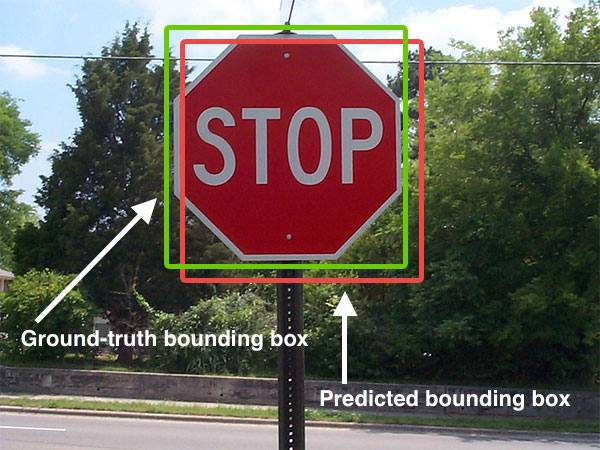
Snake (computer Vision)
Active contour model, also called snakes, is a framework in computer vision introduced by Michael Kass, Andrew Witkin, and Demetri Terzopoulos for delineating an object outline from a possibly noisy 2D image. The snakes model is popular in computer vision, and snakes are widely used in applications like object tracking, shape recognition, segmentation, edge detection and stereo matching. A snake is an energy minimizing, deformable spline influenced by constraint and image forces that pull it towards object contours and internal forces that resist deformation. Snakes may be understood as a special case of the general technique of matching a deformable model to an image by means of energy minimization. In two dimensions, the active shape model represents a discrete version of this approach, taking advantage of the point distribution model to restrict the shape range to an explicit domain learnt from a training set. Snakes do not solve the entire problem of finding contours in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Computer Vision
Computer vision tasks include methods for image sensor, acquiring, Image processing, processing, Image analysis, analyzing, and understanding digital images, and extraction of high-dimensional data from the real world in order to produce numerical or symbolic information, e.g. in the form of decisions. "Understanding" in this context signifies the transformation of visual images (the input to the retina) into descriptions of the world that make sense to thought processes and can elicit appropriate action. This image understanding can be seen as the disentangling of symbolic information from image data using models constructed with the aid of geometry, physics, statistics, and learning theory. The scientific discipline of computer vision is concerned with the theory behind artificial systems that extract information from images. Image data can take many forms, such as video sequences, views from multiple cameras, multi-dimensional data from a 3D scanning, 3D scanner, 3D point clouds ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Gradient Descent
Gradient descent is a method for unconstrained mathematical optimization. It is a first-order iterative algorithm for minimizing a differentiable multivariate function. The idea is to take repeated steps in the opposite direction of the gradient (or approximate gradient) of the function at the current point, because this is the direction of steepest descent. Conversely, stepping in the direction of the gradient will lead to a trajectory that maximizes that function; the procedure is then known as ''gradient ascent''. It is particularly useful in machine learning for minimizing the cost or loss function. Gradient descent should not be confused with local search algorithms, although both are iterative methods for optimization. Gradient descent is generally attributed to Augustin-Louis Cauchy, who first suggested it in 1847. Jacques Hadamard independently proposed a similar method in 1907. Its convergence properties for non-linear optimization problems were first studied by Has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Boundary Vector Field
The boundary vector fieldK.W. Sum, 2007 (BVF) is an external force for parametric active contours (i.e. Snakes). In the fields of computer vision and image processing, parametric active contours are widely used for segmentation and object extraction. The active contours move progressively towards its target based on the external forces. There are a number of shortcomings in using the traditional external forces, including the capture range problem, the concave object extraction problem, and high computational requirements. The BVF is generated by an interpolation In the mathematics, mathematical field of numerical analysis, interpolation is a type of estimation, a method of constructing (finding) new data points based on the range of a discrete set of known data points. In engineering and science, one ... scheme which reduces the computational requirement significantly, and at the same time, improves the capture range and concave object extraction capability. The BVF is al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Max-flow Min-cut Theorem
In computer science and optimization theory, the max-flow min-cut theorem states that in a flow network, the maximum amount of flow passing from the ''source'' to the ''sink'' is equal to the total weight of the edges in a minimum cut, i.e., the smallest total weight of the edges which if removed would disconnect the source from the sink. For example, imagine a network of pipes carrying water from a reservoir (the source) to a city (the sink). Each pipe has a capacity representing the maximum amount of water that can flow through it per unit of time. The max-flow min-cut theorem tells us that the maximum amount of water that can reach the city is limited by the smallest total capacity of any set of pipes that, if cut, would completely isolate the reservoir from the city. This smallest total capacity is the min-cut. So, if there's a bottleneck in the pipe network, represented by a small min-cut, that bottleneck will determine the overall maximum flow of water to the city. This is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Graph Cuts In Computer Vision
As applied in the field of computer vision, graph cut optimization can be employed to efficiently solve a wide variety of low-level computer vision problems (''early vision''), such as image smoothing, the stereo correspondence problem, image segmentation, object co-segmentation, and many other computer vision problems that can be formulated in terms of energy minimization. Many of these energy minimization problems can be approximated by solving a maximum flow problem in a graph (and thus, by the max-flow min-cut theorem, define a minimal cut of the graph). Under most formulations of such problems in computer vision, the minimum energy solution corresponds to the maximum a posteriori estimate of a solution. Although many computer vision algorithms involve cutting a graph (e.g., normalized cuts), the term "graph cuts" is applied specifically to those models which employ a max-flow/min-cut optimization (other graph cutting algorithms may be considered as graph partitioning ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Allen Tannenbaum
Allen Robert Tannenbaum (January 25, 1953 – ) was an American applied mathematician who finished his career as a Distinguished Professor in the Departments of Computer Science and Applied Mathematics & Statistics at the State University of New York at Stony Brook. Tannenbaum's research covered numerous areas, including robust control, computer vision, biomedical imaging, and bioinformatics, totaling almost 500 publications. Research He pioneered the field of robust control with the solution of the gain margin and phase margin problems using techniques from Nevanlinna–Pick interpolation theory, which was the first H-infinity type control problem solved. Tannenbaum used techniques from elliptic curves to show that the reachability does not imply pole assignability for systems defined over polynomial rings in two or more variables over an arbitrary field. He pioneered the use of partial differential equations in computer vision and biomedical imaging co-inventing with Guille ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Signed Distance Function
In mathematics and its applications, the signed distance function or signed distance field (SDF) is the orthogonal distance of a given point ''x'' to the boundary of a set Ω in a metric space (such as the surface of a geometric shape), with the sign determined by whether or not ''x'' is in the interior of Ω. The function has positive values at points ''x'' inside Ω, it decreases in value as ''x'' approaches the boundary of Ω where the signed distance function is zero, and it takes negative values outside of Ω. However, the alternative convention is also sometimes taken instead (i.e., negative inside Ω and positive outside). The concept also sometimes goes by the name oriented distance function/field. Definition Let be a subset of a metric space with metric , and \partial\Omega be its boundary. The distance between a point of and the subset \partial\Omega of is defined as usual as : d(x, \partial \Omega) = \inf_d(x, y), where \inf denotes the infimum. The ''sign ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Medical Image Computing
Medical image computing (MIC) is an interdisciplinary field at the intersection of computer science Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ..., information engineering, electrical engineering, physics, mathematics and medicine. This field develops computational and mathematical methods for solving problems pertaining to medical images and their use for biomedical research and clinical care. The main goal of MIC is to extract clinically relevant information or knowledge from medical images. While closely related to the field of medical imaging, MIC focuses on the computational analysis of the images, not their acquisition. The methods can be grouped into several broad categories: image segmentation, image registration, image-based physiological modeling, and others. Data f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Level Sets
Level or levels may refer to: Engineering *Level (optical instrument), a device used to measure true horizontal or relative heights * Spirit level or bubble level, an instrument designed to indicate whether a surface is horizontal or vertical *Canal pound or level * Regrading or levelling, the process of raising and/or lowering the levels of land * Storey or level, a vertical unit of a building or a mine * Level (coordinate), vertical position * Horizontal plane parallel Gaming * Level (video games), a stage of the game * Level (role-playing games), a measurement of character development Music * Level (music), similar to but more general and basic than a chord * "Level" (The Raconteurs song) * ''Levels'' (album), an album by AKA * "Levels" (Avicii song) * "Levels" (Bilal song) * "Levels" (Nick Jonas song) * "Levels" (Meek Mill song) * "Levels" (NorthSideBenji song), featuring Houdini * "Levels" (Sidhu Moose Wala song) Places * Level Mountain, a volcano in northern British Colum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Curve-shortening Flow
In mathematics, the curve-shortening flow is a process that modifies a smooth curve in the Euclidean plane by moving its points perpendicularly to the curve at a speed proportional to the curvature. The curve-shortening flow is an example of a geometric flow, and is the one-dimensional case of the mean curvature flow. Other names for the same process include the Euclidean shortening flow, geometric heat flow, and arc length evolution. As the points of any smooth simple closed curve move in this way, the curve remains simple and smooth. It loses area at a constant rate, and its perimeter decreases as quickly as possible for any continuous curve evolution. If the curve is non-convex, its total absolute curvature decreases monotonically, until it becomes convex. Once convex, the isoperimetric ratio of the curve decreases as the curve converges to a circular shape, before collapsing to a singularity. If two disjoint simple smooth closed curves evolve, they remain disjoint until ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mumford–Shah Functional
The Mumford–Shah functional is a functional that is used to establish an optimality criterion for segmenting an image into sub-regions. An image is modeled as a piecewise-smooth function. The functional penalizes the distance between the model and the input image, the lack of smoothness of the model within the sub-regions, and the length of the boundaries of the sub-regions. By minimizing the functional one may compute the best image segmentation. The functional was proposed by mathematicians David Mumford and Jayant Shah in 1989.. Definition of the Mumford–Shah functional Consider an image ''I'' with a domain of definition ''D'', call ''J'' the image's model, and call ''B'' the boundaries that are associated with the model: the Mumford–Shah functional ''E'' ''J'',''B'' is defined as : E ,B= \alpha \int_D (I(\vec x) - J(\vec x))^2 \,\mathrm\vec x + \beta \int _ \vec \nabla J(\vec x) \cdot \vec \nabla J(\vec x) \,\mathrm \vec x + \gamma \int _B ds Optimization of the fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |