|
Small Ditrigonal Icosidodecahedron
In geometry, the small ditrigonal icosidodecahedron (or small ditrigonary icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U30. It has 32 faces (20 triangles and 12 pentagrams), 60 edges, and 20 vertices. It has extended Schläfli symbol a, as an ''altered dodecahedron'', and Coxeter diagram or . It is constructed from Schwarz triangle (3 3 ) with Wythoff symbol 3 , 3. Its hexagonal vertex figure alternates equilateral triangle and pentagram faces. Related polyhedra Its convex hull is a regular dodecahedron. It additionally shares its edge arrangement with the great ditrigonal icosidodecahedron (having the triangular faces in common), the ditrigonal dodecadodecahedron (having the pentagrammic faces in common), and the regular compound of five cubes. As a simple polyhedron, it is also a hexakis truncated icosahedron where the triangles touching the pentagons are made coplanar, making the others concave. See also * List of uniform polyhedra In geometry, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small Ditrigonal Icosidodecahedron
In geometry, the small ditrigonal icosidodecahedron (or small ditrigonary icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U30. It has 32 faces (20 triangles and 12 pentagrams), 60 edges, and 20 vertices. It has extended Schläfli symbol a, as an ''altered dodecahedron'', and Coxeter diagram or . It is constructed from Schwarz triangle (3 3 ) with Wythoff symbol 3 , 3. Its hexagonal vertex figure alternates equilateral triangle and pentagram faces. Related polyhedra Its convex hull is a regular dodecahedron. It additionally shares its edge arrangement with the great ditrigonal icosidodecahedron (having the triangular faces in common), the ditrigonal dodecadodecahedron (having the pentagrammic faces in common), and the regular compound of five cubes. As a simple polyhedron, it is also a hexakis truncated icosahedron where the triangles touching the pentagons are made coplanar, making the others concave. See also * List of uniform polyhedra In geometry, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dodecahedron
In geometry, a dodecahedron (Greek , from ''dōdeka'' "twelve" + ''hédra'' "base", "seat" or "face") or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120. Some dodecahedra have the same combinatorial structure as the regular dodecahedron (in terms of the graph formed by its vertices and edges), but their pentagonal faces are not regular: The pyritohedron, a common crystal form in pyrite, has pyritohedral symmetry, while the tetartoid has tetrahedral symmetry. The rhombic dodecahedron can be seen as a limiting case of the pyritohedron, and it has octahedral symmetry. The elongated dodecahedron and trapezo-rhombic dodecahedron variations, along with the rhombic dodecahedra, are space-filling. There ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
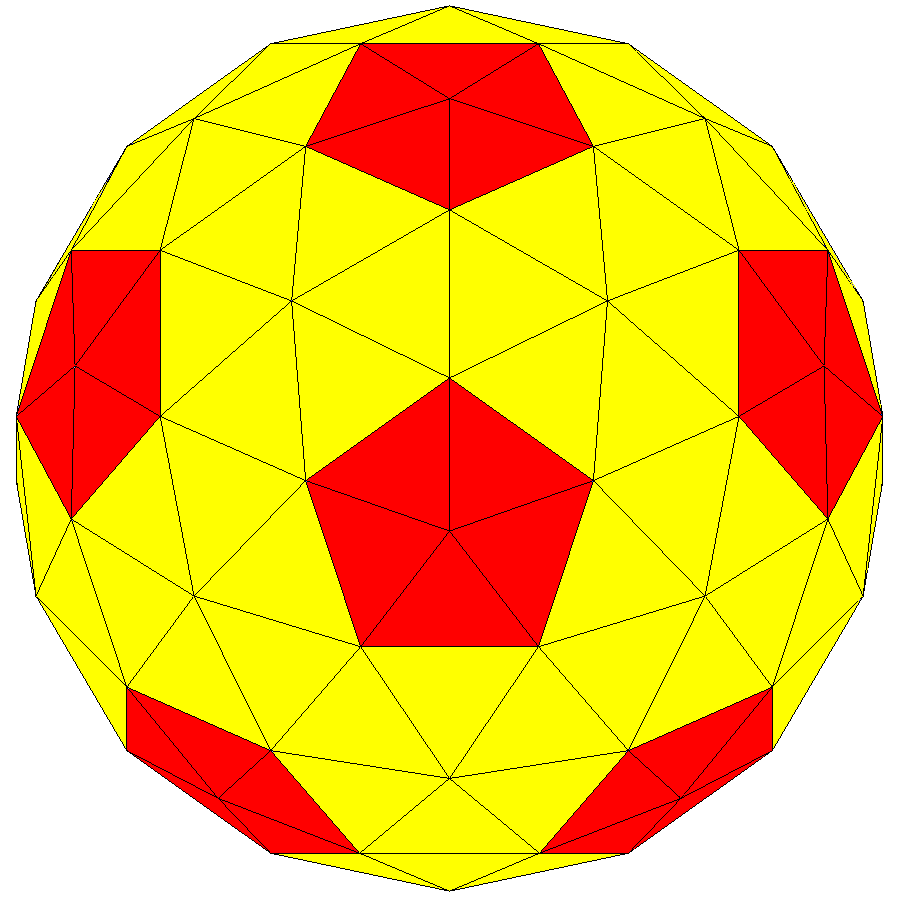
Spherical Compound Of Five Cubes
A sphere () is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. A sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the centre of the sphere, and is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians. The sphere is a fundamental object in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. Basic terminology As mentioned earlier is the spher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Five Cubes
The compound of five cubes is one of the five regular polyhedral compounds. It was first described by Edmund Hess in 1876. It is one of five regular compounds, and dual to the compound of five octahedra. It can be seen as a faceting of a regular dodecahedron. It is one of the stellations of the rhombic triacontahedron. It has icosahedral symmetry (Ih). Geometry The compound is a faceting of a dodecahedron (where pentagrams can be seen correlating to the pentagonal faces). Each cube represents a selection of 8 of the 20 vertices of the dodecahedron. If the shape is considered as a union of five cubes yielding a simple nonconvex solid without self-intersecting surfaces, then it has 360 faces (all triangles), 182 vertices (60 with degree 3, 30 with degree 4, 12 with degree 5, 60 with degree 8, and 20 with degree 12), and 540 edges, yielding an Euler characteristic of 182 − 540 + 360 = 2. Edge arrangement Its convex hull is a regular dodecahedron. It additionally shares ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dodecahedron
In geometry, a dodecahedron (Greek , from ''dōdeka'' "twelve" + ''hédra'' "base", "seat" or "face") or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120. Some dodecahedra have the same combinatorial structure as the regular dodecahedron (in terms of the graph formed by its vertices and edges), but their pentagonal faces are not regular: The pyritohedron, a common crystal form in pyrite, has pyritohedral symmetry, while the tetartoid has tetrahedral symmetry. The rhombic dodecahedron can be seen as a limiting case of the pyritohedron, and it has octahedral symmetry. The elongated dodecahedron and trapezo-rhombic dodecahedron variations, along with the rhombic dodecahedra, are space-filling. There ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ditrigonal Dodecadodecahedron
In geometry, the ditrigonal dodecadodecahedron (or ditrigonary dodecadodecahedron) is a nonconvex uniform polyhedron, indexed as U41. It has 24 faces (12 pentagons and 12 pentagrams), 60 edges, and 20 vertices. It has extended Schläfli symbol b, as a ''blended great dodecahedron'', and Coxeter diagram . It has 4 Schwarz triangle equivalent constructions, for example Wythoff symbol 3 , 5, and Coxeter diagram . Related polyhedra Its convex hull is a regular dodecahedron. It additionally shares its edge arrangement with the small ditrigonal icosidodecahedron (having the pentagrammic faces in common), the great ditrigonal icosidodecahedron (having the pentagonal faces in common), and the regular compound of five cubes. Furthermore, it may be viewed as a facetted dodecahedron: the pentagrammic faces are inscribed in the dodecahedron's pentagons. Its dual, the medial triambic icosahedron, is a stellation of the icosahedron. It is topologically equivalent to a quotient sp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Ditrigonal Icosidodecahedron
In geometry, the great ditrigonal icosidodecahedron (or great ditrigonary icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U47. It has 32 faces (20 triangles and 12 pentagons), 60 edges, and 20 vertices. It has 4 Schwarz triangle equivalent constructions, for example Wythoff symbol 3 , 3 gives Coxeter diagram = . It has extended Schläfli symbol a or c, as an ''altered great stellated dodecahedron'' or ''converted great icosahedron''. Its circumradius is \frac times the length of its edge, a value it shares with the cube. Related polyhedra Its convex hull is a regular dodecahedron. It additionally shares its edge arrangement with the small ditrigonal icosidodecahedron (having the triangular faces in common), the ditrigonal dodecadodecahedron (having the pentagonal faces in common), and the regular compound of five cubes The compound of five cubes is one of the five regular polyhedral compounds. It was first described by Edmund Hess in 1876. It is one ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ditrigonal Dodecadodecahedron Cd
In geometry, there are seven uniform and uniform dual polyhedra named as ditrigonal. Ditrigonal vertex figures There are five uniform ditrigonal polyhedra, all with icosahedral symmetry.Har'El, 1993 The three uniform star polyhedron with Wythoff symbol of the form 3 , ''p'' ''q'' or , ''p'' ''q'' are ditrigonal, at least if ''p'' and ''q'' are not 2. Each polyhedron includes two types of faces, being of triangles, pentagons, or pentagrams. Their vertex configurations are of the form ''p''.''q''.''p''.''q''.''p''.''q'' or (''p''.''q'')3 with a symmetry of order 3. Here, term ditrigonal refers to a hexagon having a symmetry of order 3 (triangular symmetry) acting with 2 rotational orbits on the 6 angles of the vertex figure (the word ''ditrigonal'' means "having two sets of 3 angles"). Mathworld (retrieved 10 June 2016) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexakis Truncated Icosahedron
The hexapentakis truncated icosahedron is a convex set, convex polyhedron constructed as an augmentation (geometry), augmented truncated icosahedron. It is geodesic polyhedron 3,0, with pentavalent vertices separated by an edge-direct distance of 3 steps. Construction Geodesic polyhedra are constructed by subdividing faces of simpler polyhedra, and then projecting the new vertices onto the surface of a sphere. A geodesic polyhedron has straight edges and flat faces that approximate a sphere, but it can also be made as a spherical polyhedron (A tessellation on a sphere) with true geodesic curved edges on the surface of a sphere. and spherical triangle faces. Related polyhedra Pentakis truncated icosahedron The pentakis truncated icosahedron is a convex set, convex polyhedron constructed as an augmentation (geometry), augmented truncated icosahedron, adding pyramids to the 12 pentagonal faces, creating 60 new triangular faces. It is geometrically similar to the icosahedron w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
