|
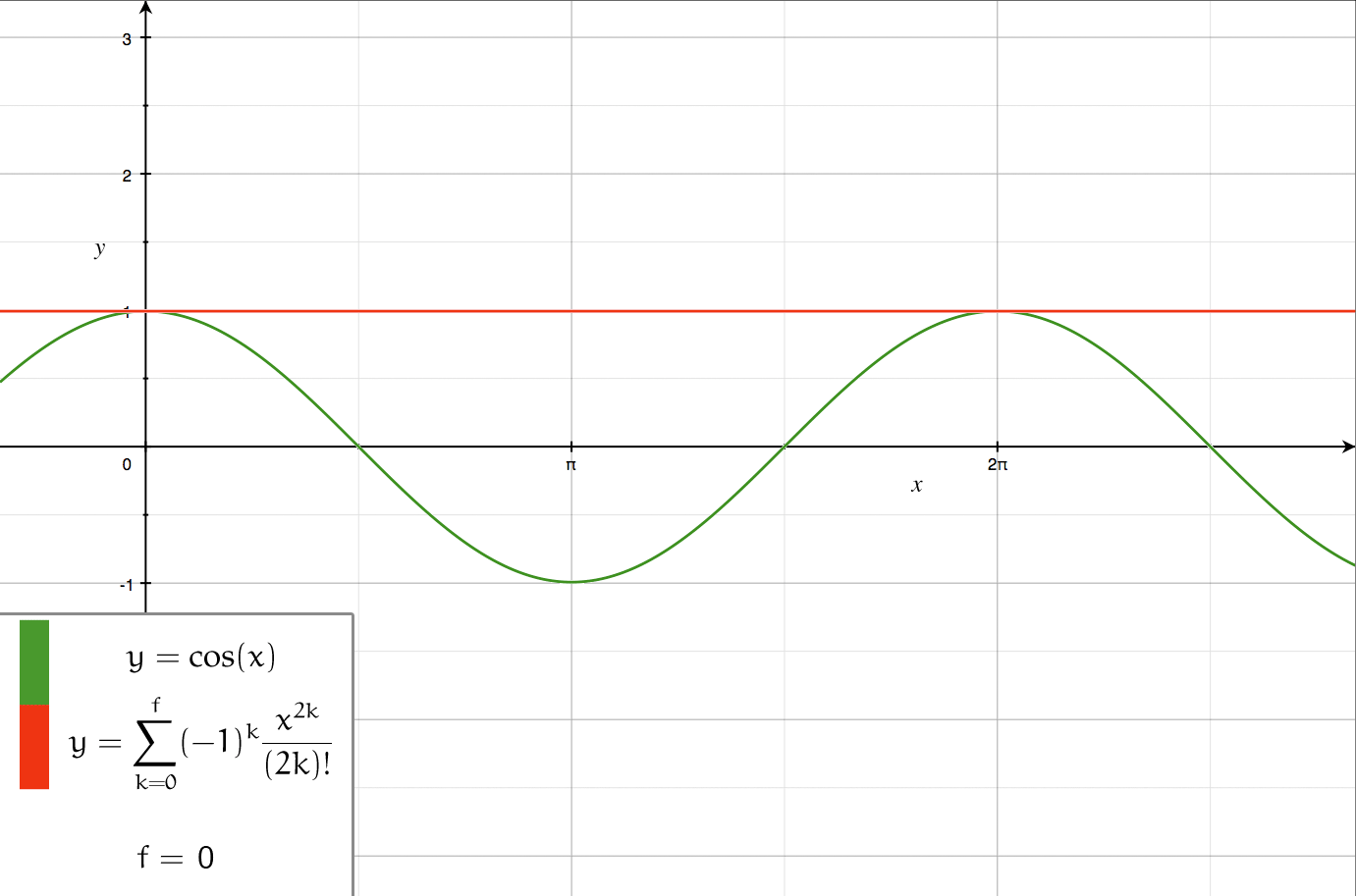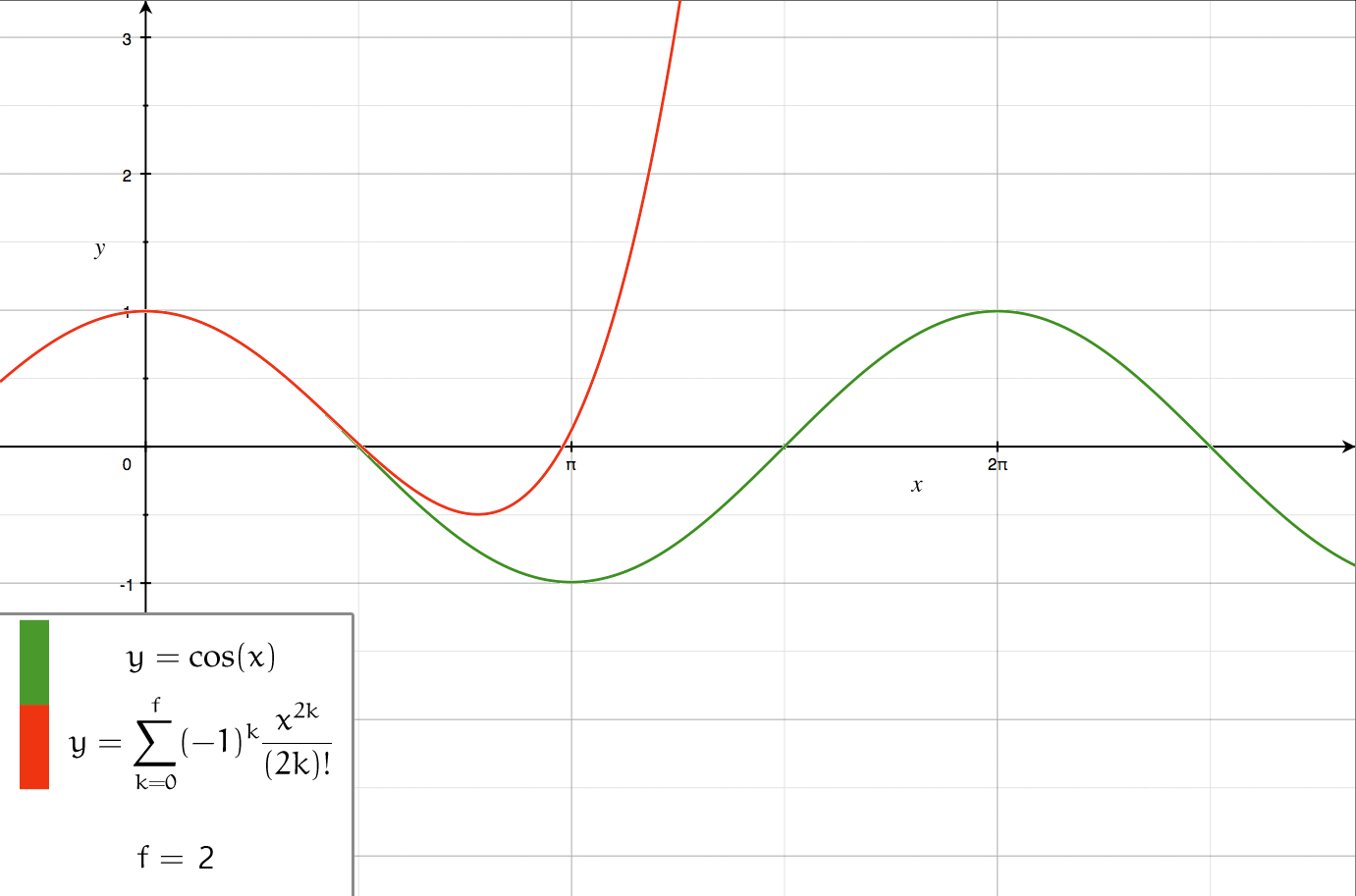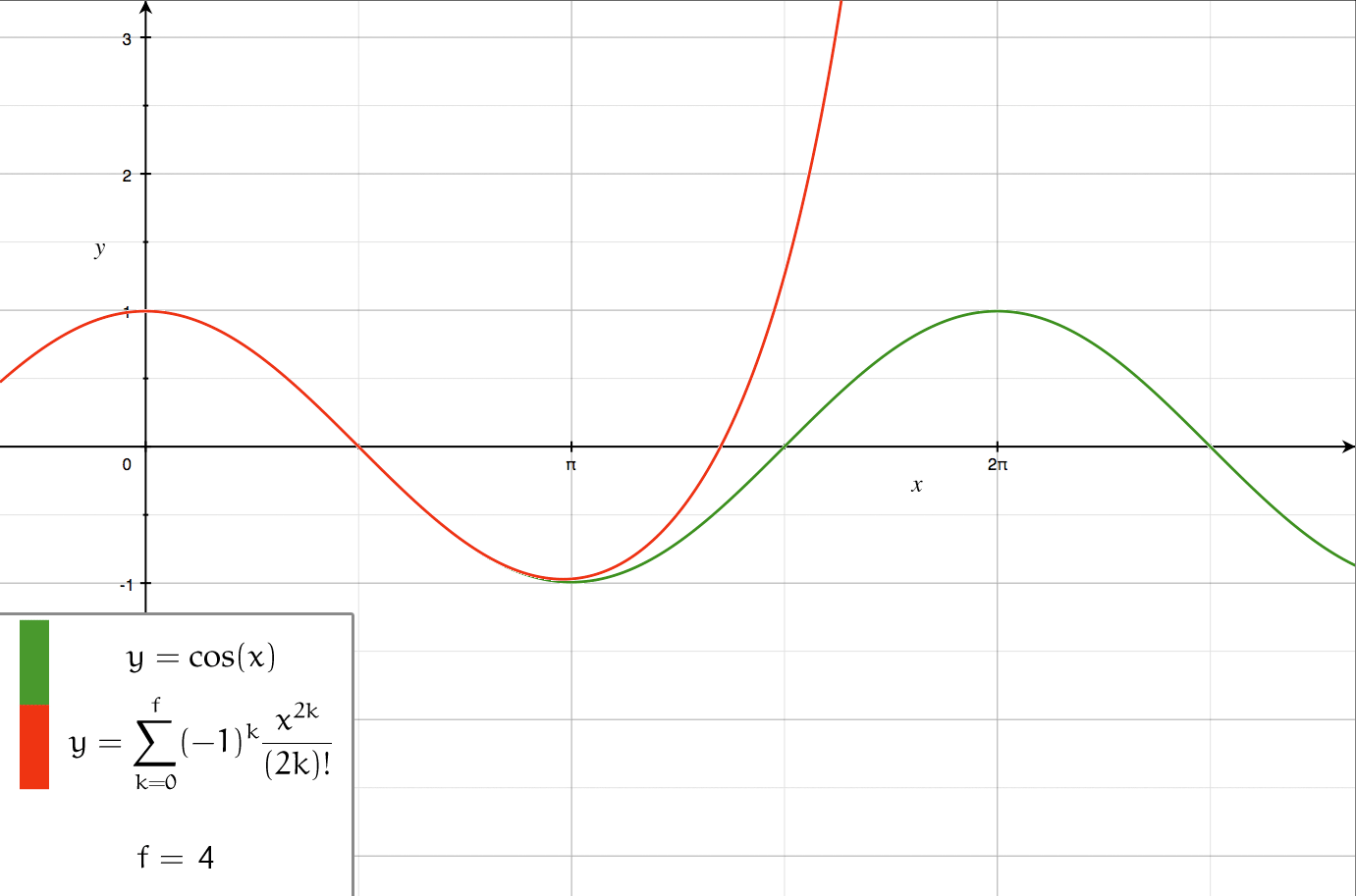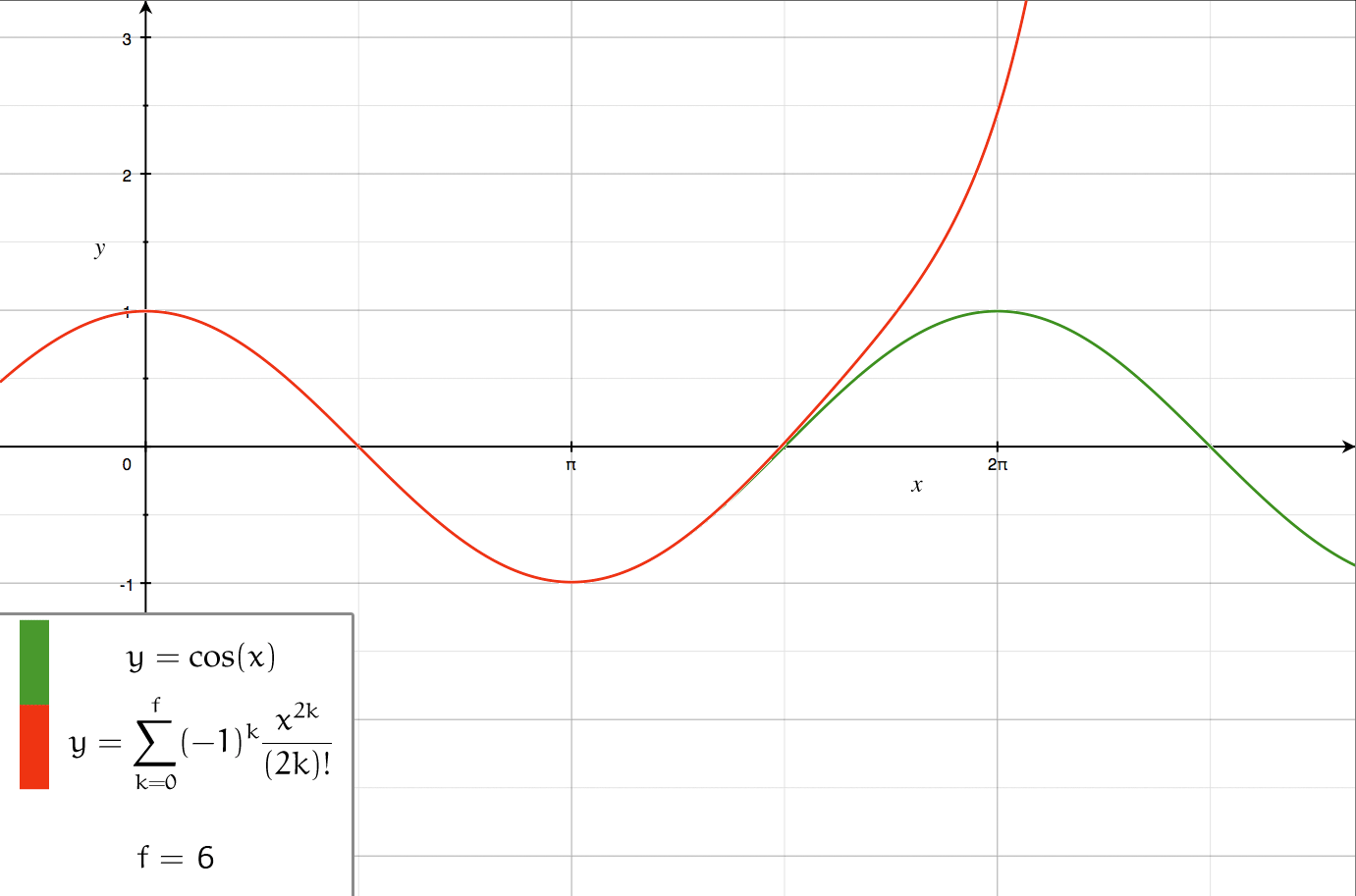
Series Expansion
In mathematics, a series expansion is an expansion of a function into a series, or infinite sum. It is a method for calculating a function that cannot be expressed by just elementary operators (addition, subtraction, multiplication and division). The resulting so-called ''series'' often can be limited to a finite number of terms, thus yielding an approximation of the function. The fewer terms of the sequence are used, the simpler this approximation will be. Often, the resulting inaccuracy (i.e., the partial sum of the omitted terms) can be described by an equation involving Big O notation (see also asymptotic expansion). The series expansion on an open interval will also be an approximation for non-analytic functions. Types of series expansions There are several kinds of series expansions, listed below. A ''Taylor series'' is a power series based on a function's derivatives at a single point. More specifically, if a function f: U\to\mathbb is infinitely differentiable around ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Cos
Taylor, Taylors or Taylor's may refer to: People * Taylor (surname) **List of people with surname Taylor * Taylor (given name), including Tayla and Taylah * Taylor sept, a branch of Scottish clan Cameron * Justice Taylor (other) Places Australia * Electoral district of Taylor, South Australia * Taylor, Australian Capital Territory, planned suburb Canada * Taylor, British Columbia United States * Taylor, Alabama * Taylor, Arizona * Taylor, Arkansas * Taylor, Indiana * Taylor, Louisiana * Taylor, Maryland * Taylor, Michigan * Taylor, Mississippi * Taylor, Missouri * Taylor, Nebraska * Taylor, North Dakota * Taylor, New York * Taylor, Beckham County, Oklahoma * Taylor, Cotton County, Oklahoma * Taylor, Pennsylvania * Taylors, South Carolina * Taylor, Texas * Taylor, Utah * Taylor, Washington * Taylor, West Virginia * Taylor, Wisconsin * Taylor, Wyoming * Taylor County (other) * Taylor Township (other) Businesses and organisations * Taylor's (d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirichlet Series
In mathematics, a Dirichlet series is any series of the form \sum_^\infty \frac, where ''s'' is complex, and a_n is a complex sequence. It is a special case of general Dirichlet series. Dirichlet series play a variety of important roles in analytic number theory. The most usually seen definition of the Riemann zeta function is a Dirichlet series, as are the Dirichlet L-functions. It is conjectured that the Selberg class of series obeys the generalized Riemann hypothesis. The series is named in honor of Peter Gustav Lejeune Dirichlet. Combinatorial importance Dirichlet series can be used as generating series for counting weighted sets of objects with respect to a weight which is combined multiplicatively when taking Cartesian products. Suppose that ''A'' is a set with a function ''w'': ''A'' → N assigning a weight to each of the elements of ''A'', and suppose additionally that the Fiber (mathematics), fibre over any natural number under that weight is a finite set. (We call such ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multipole Expansion
A multipole expansion is a mathematical series representing a function that depends on angles—usually the two angles used in the spherical coordinate system (the polar and azimuthal angles) for three-dimensional Euclidean space, \R^3. Similarly to Taylor series, multipole expansions are useful because oftentimes only the first few terms are needed to provide a good approximation of the original function. The function being expanded may be real- or complex-valued and is defined either on \R^3, or less often on \R^n for some other Multipole expansions are used frequently in the study of electromagnetic and gravitational fields, where the fields at distant points are given in terms of sources in a small region. The multipole expansion with angles is often combined with an expansion in radius. Such a combination gives an expansion describing a function throughout three-dimensional space. The multipole expansion is expressed as a sum of terms with progressively finer angular featur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadrupole
A quadrupole or quadrapole is one of a sequence of configurations of things like electric charge or current, or gravitational mass that can exist in ideal form, but it is usually just part of a multipole expansion of a more complex structure reflecting various orders of complexity. Mathematical definition The quadrupole moment tensor ''Q'' is a rank-two tensor—3×3 matrix. There are several definitions, but it is normally stated in the traceless form (i.e. Q_ + Q_ + Q_ = 0). The quadrupole moment tensor has thus nine components, but because of transposition symmetry and Trace (linear algebra), zero-trace property, in this form only five of these are independent. For a discrete system of \ell point charges or masses in the case of a Quadrupole#Gravitational quadrupole, gravitational quadrupole, each with charge q_\ell, or mass m_\ell, and position \vec_\ell = \left(r_, r_, r_\right) relative to the coordinate system origin, the components of the ''Q'' matrix are defined by: : ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dipole
In physics, a dipole () is an electromagnetic phenomenon which occurs in two ways: *An electric dipole deals with the separation of the positive and negative electric charges found in any electromagnetic system. A simple example of this system is a pair of charges of equal magnitude but opposite sign separated by some typically small distance. (A permanent electric dipole is called an electret.) *A magnetic dipole is the closed circulation of an electric current system. A simple example is a single loop of wire with constant current through it. A bar magnet is an example of a magnet with a permanent magnetic dipole moment. Dipoles, whether electric or magnetic, can be characterized by their dipole moment, a vector quantity. For the simple electric dipole, the electric dipole moment points from the negative charge towards the positive charge, and has a magnitude equal to the strength of each charge times the separation between the charges. (To be precise: for the definition of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superposition Principle
The superposition principle, also known as superposition property, states that, for all linear systems, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually. So that if input ''A'' produces response ''X'' and input ''B'' produces response ''Y'' then input (''A'' + ''B'') produces response (''X'' + ''Y''). A function F(x) that satisfies the superposition principle is called a linear function. Superposition can be defined by two simpler properties: additivity F(x_1+x_2)=F(x_1)+F(x_2) \, and homogeneity F(a x)=a F(x) \, for scalar . This principle has many applications in physics and engineering because many physical systems can be modeled as linear systems. For example, a beam can be modeled as a linear system where the input stimulus is the load on the beam and the output response is the deflection of the beam. The importance of linear systems is that they are easier to analyze mathematically; the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." Physics is one of the most fundamental scientific disciplines, with its main goal being to understand how the universe behaves. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Legendre Polynomials
In physical science and mathematics, Legendre polynomials (named after Adrien-Marie Legendre, who discovered them in 1782) are a system of complete and orthogonal polynomials, with a vast number of mathematical properties, and numerous applications. They can be defined in many ways, and the various definitions highlight different aspects as well as suggest generalizations and connections to different mathematical structures and physical and numerical applications. Closely related to the Legendre polynomials are associated Legendre polynomials, Legendre functions, Legendre functions of the second kind, and associated Legendre functions. Definition by construction as an orthogonal system In this approach, the polynomials are defined as an orthogonal system with respect to the weight function w(x) = 1 over the interval 1,1/math>. That is, P_n(x) is a polynomial of degree n, such that \int_^1 P_m(x) P_n(x) \,dx = 0 \quad \text n \ne m. With the additional standardization co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Table Of Newtonian Series
In mathematics, a Newtonian series, named after Isaac Newton, is a sum over a sequence a_n written in the form :f(s) = \sum_^\infty (-1)^n a_n = \sum_^\infty \frac a_n where : is the binomial coefficient and (s)_n is the falling factorial. Newtonian series often appear in relations of the form seen in umbral calculus. List The generalized binomial theorem gives : (1+z)^s = \sum_^z^n = 1+z+z^2+\cdots. A proof for this identity can be obtained by showing that it satisfies the differential equation : (1+z) \frac = s (1+z)^s. The digamma function: :\psi(s+1)=-\gamma-\sum_^\infty \frac . The Stirling numbers of the second kind are given by the finite sum :\left\ =\frac\sum_^(-1)^ j^n. This formula is a special case of the ''k''th forward difference of the monomial ''x''''n'' evaluated at ''x'' = 0: : \Delta^k x^n = \sum_^(-1)^ (x+j)^n. A related identity forms the basis of the Nörlund–Rice integral: :\sum_^n \frac = \frac = \frac= B(n+1,s-n),s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Overtone
An overtone is any resonant frequency above the fundamental frequency of a sound. (An overtone may or may not be a harmonic) In other words, overtones are all pitches higher than the lowest pitch within an individual sound; the fundamental is the lowest pitch. While the fundamental is usually heard most prominently, overtones are actually present in any pitch except a true sine wave. The relative volume or amplitude of various overtone partials is one of the key identifying features of timbre, or the individual characteristic of a sound. Using the model of Fourier analysis, the fundamental and the overtones together are called partials. Harmonics, or more precisely, harmonic partials, are partials whose frequencies are numerical integer multiples of the fundamental (including the fundamental, which is 1 times itself). These overlapping terms are variously used when discussing the acoustic behavior of musical instruments. Alexander J. Ellis (translating Hermann von Helmholtz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Frequency
The fundamental frequency, often referred to simply as the ''fundamental'', is defined as the lowest frequency of a periodic waveform. In music, the fundamental is the musical pitch of a note that is perceived as the lowest partial present. In terms of a superposition of sinusoids, the fundamental frequency is the lowest frequency sinusoidal in the sum of harmonically related frequencies, or the frequency of the difference between adjacent frequencies. In some contexts, the fundamental is usually abbreviated as 0, indicating the lowest frequency counting from zero. In other contexts, it is more common to abbreviate it as 1, the first harmonic. (The second harmonic is then 2 = 2⋅1, etc. In this context, the zeroth harmonic would be 0 Hz.) According to Benward's and Saker's ''Music: In Theory and Practice'': Explanation All sinusoidal and many non-sinusoidal waveforms repeat exactly over time – they are periodic. The period of a waveform is the smallest value of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acoustics
Acoustics is a branch of physics that deals with the study of mechanical waves in gases, liquids, and solids including topics such as vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics technology may be called an Acoustical engineering, acoustical engineer. The application of acoustics is present in almost all aspects of modern society with the most obvious being the audio and noise control industries. Hearing (sense), Hearing is one of the most crucial means of survival in the animal world and speech is one of the most distinctive characteristics of human development and culture. Accordingly, the science of acoustics spreads across many facets of human society—music, medicine, architecture, industrial production, warfare and more. Likewise, animal species such as songbirds and frogs use sound and hearing as a key element of mating rituals or for marking territories. Art, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |