|
Septimal Quarter Tone
A septimal quarter tone (in music) is an interval with the ratio of 36:35, which is the difference between the septimal minor third and the Just minor third, or about 48.77 cents wide. The name derives from the interval being the 7-limit approximation of a quarter tone. The septimal quarter tone can be viewed either as a musical interval in its own right, or as a comma; if it is tempered out in a given tuning system, the distinction between the two different types of minor thirds is lost. The septimal quarter tone may be derived from the harmonic series as the interval between the thirty-fifth and thirty-sixth harmonics. Composer Ben Johnston uses a small seven ("") as an accidental to indicate a note is lowered by 36/35 (≈49 cents), or an upside-down seven ("") to indicate a note is raised by the same amount."Ben Johnston's Extended Just Intonation – A Guide for Interpreters", John Fonville, p. 113, ''Perspectives of New Music'', vol. 29, no. 2 (Summer, 1991), pp. 10 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quarter Tone On C Sharps
A quarter is one-fourth, , 25% or 0.25. Quarter or quarters may refer to: Places * Quarter (urban subdivision), a section or area, usually of a town Placenames * Quarter, South Lanarkshire, a settlement in Scotland * Le Quartier, a settlement in France * The Quarter, Anguilla * Quartier, Sud, Haiti Arts, entertainment, and media * Quarters (children's game) or bloody knuckles, a schoolyard game involving quarters or other coins * Quarters (game), a drinking game * ''Quarters!'', a 2015 album by the psychedelic rock group King Gizzard and the Lizard Wizard * Quarter note, in music one quarter of a whole note * "Quarters" (Wilco song) * "Quarter" (song) Coins * Quarter (Canadian coin), valued at one-fourth of a Canadian dollar * Quarter (United States coin), valued at one-fourth of a U.S. dollar ** Washington quarter, the current design of this coin * Quarter farthing, a British monetary unit * Quarter dollar, unit of currencies that are named dollar * Quarter guinea, a B ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perspectives Of New Music
''Perspectives of New Music'' (PNM) is a peer-reviewed academic journal specializing in music theory and analysis. It was established in 1962 by Arthur Berger and Benjamin Boretz (who were its initial editors-in-chief). ''Perspectives'' was first published by the Princeton University Press, initially supported by the Fromm Music Foundation.David Carson Berry, "''Journal of Music Theory'' under Allen Forte's Editorship," ''Journal of Music Theory'' 50/1 (2006), 21, n49. The first issue was favorably reviewed in the ''Journal of Music Theory'', which observed that Berger and Boretz had produced "a first issue which sustains such a high quality of interest and cogency among its articles that one suspects the long delay preceding the yet-unborn Spring 1963 issue may reflect a scarcity of material up to their standard". However, as the journal's editorial "perspective" coalesced, Fromm became—in the words of David Gable—disenchanted with the "exclusive viewpoint hatcame to domina ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Commas (music)
The comma is a punctuation mark that appears in several variants in different languages. It has the same shape as an apostrophe or single closing quotation mark () in many typefaces, but it differs from them in being placed on the baseline of the text. Some typefaces render it as a small line, slightly curved or straight, but inclined from the vertical. Other fonts give it the appearance of a miniature filled-in figure on the baseline. The comma is used in many contexts and languages, mainly to separate parts of a sentence such as clauses, and items in lists mainly when there are three or more items listed. The word ''comma'' comes from the Greek (), which originally meant a cut-off piece, specifically in grammar, a short clause. A comma-shaped mark is used as a diacritic in several writing systems and is considered distinct from the cedilla. In Byzantine and modern copies of Ancient Greek, the " rough" and "smooth breathings" () appear above the letter. In Latvian, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
7-limit Tuning And Intervals
7-limit or septimal tunings and intervals are musical instrument tunings that have a limit of seven: the largest prime factor contained in the interval ratios between pitches is seven. Thus, for example, 50:49 is a 7-limit interval, but 14:11 is not. For example, the greater just minor seventh, 9:5 () is a 5-limit ratio, the harmonic seventh has the ratio 7:4 and is thus a septimal interval. Similarly, the septimal chromatic semitone, 21:20, is a septimal interval as 21÷7=3. The harmonic seventh is used in the barbershop seventh chord and music. () Compositions with septimal tunings include La Monte Young's ''The Well-Tuned Piano'', Ben Johnston's String Quartet No. 4, Lou Harrison's ''Incidental Music for Corneille's Cinna'', and Michael Harrison's ''Revelation: Music in Pure Intonation''. The Great Highland bagpipe is tuned to a ten-note seven-limit scale: 1:1, 9:8, 5:4, 4:3, 27:20, 3:2, 5:3, 7:4, 16:9, 9:5. In the 2nd century Ptolemy described the septimal i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Seventh
The harmonic seventh interval, also known as the septimal minor seventh, or subminor seventh, is one with an exact 7:4 ratio (about 969 cent (music), cents). This is somewhat narrower than and is, "particularly sweet", "sweeter in quality" than an "ordinary" minor seventh, just minor seventh, which has an intonation ratio of 9:5 (about 1018 cents). The harmonic seventh arises from the Harmonic series (music), harmonic series as the interval between the fourth harmonic (second octave of the fundamental) and the seventh harmonic; in that octave, harmonics 4, 5, 6, and 7 constitute a purely consonant major chord with added seventh (root position). When played on the natural horn, as a compromise the note is often adjusted to 16:9 of the root (for C maj7, the substituted note is B, 996.09 cents), but some pieces call for the pure harmonic seventh, including Benjamin Britten, Britten's ''Serenade for Tenor, Horn and Strings''. Composer Ben Johnston (composer), Ben ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minor Seventh
In music theory, a minor seventh is one of two musical intervals that span seven staff positions. It is ''minor'' because it is the smaller of the two sevenths, spanning ten semitones. The major seventh spans eleven. For example, the interval from A to G is a minor seventh, as the note G lies ten semitones above A, and there are seven staff positions from A to G. Diminished and augmented sevenths span the same number of staff positions, but consist of a different number of semitones (nine and twelve, respectively). Minor seventh intervals rarely feature in melodies (and especially in their openings) but occur more often than major sevenths. The best-known example, in part due to its frequent use in theory classes, is found between the first two words of the phrase "There's a place for us" in the song " Somewhere" in ''West Side Story''.Neely, Blake (2009). ''Piano For Dummies'', p.201. . Another well-known example occurs between the first two notes of the introduction to the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
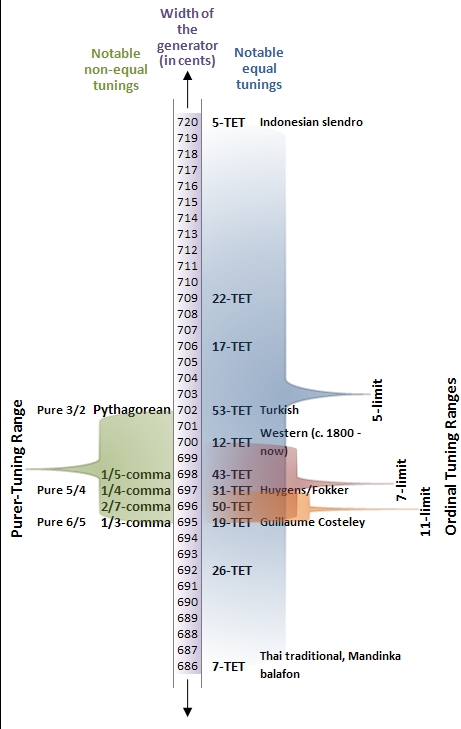
31-TET
In music, 31 equal temperament, 31-ET, which can also be abbreviated 31-TET (31 tone ET) or 31-EDO (equal division of the octave), also known as tricesimoprimal, is the tempered scale derived by dividing the octave into 31 equal-sized steps (equal frequency ratios). Each step represents a frequency ratio of , or 38.71 cents (). 31-ET is a very good approximation of quarter-comma meantone temperament. More generally, it is a regular diatonic tuning in which the tempered perfect fifth is equal to 696.77 cents, as shown in Figure 1. On an isomorphic keyboard, the fingering of music composed in 31-ET is precisely the same as it is in any other syntonic tuning (such as 12-ET), so long as the notes are spelled properly — that is, with no assumption of enharmonicity. History and use Division of the octave into 31 steps arose naturally out of Renaissance music theory; the lesser diesis — the ratio of an octave to three major thirds, 128:125 or 41.06 cents — was approxima ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
24-TET
A quarter tone is a pitch halfway between the usual notes of a chromatic scale or an interval about half as wide (aurally, or logarithmically) as a semitone, which itself is half a whole tone. Quarter tones divide the octave by 50 cents each, and have 24 different pitches. Quarter tone has its roots in the music of the Middle East and more specifically in Persian traditional music. However, the first evidenced proposal of quarter tones, or the quarter-tone scale (24 equal temperament), was made by 19th-century music theorists Heinrich Richter in 1823 Julian Rushton, "Quarter-Tone", '' The New Grove Dictionary of Music and Musicians'', second edition, edited by Stanley Sadie and John Tyrrell (London: Macmillan, 2001). and Mikhail Mishaqa about 1840. Composers who have written music using this scale include: Pierre Boulez, Julián Carrillo, Mildred Couper, George Enescu, Alberto Ginastera, Gérard Grisey, Alois Hába, Ljubica Marić, Charles Ives, Tristan Murail, Krzysz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
22-TET
In music, 22 equal temperament, called 22-TET, 22-EDO, or 22-ET, is the tempered scale derived by dividing the octave into 22 equal steps (equal frequency ratios). Each step represents a frequency ratio of , or 54.55 cents (). When composing with 22-ET, one needs to take into account a variety of considerations. Considering the 5-limit, there is a difference between 3 fifths and the sum of 1 fourth + 1 major third. It means that, starting from C, there are two A's - one 16 steps and one 17 steps away. There is also a difference between a major tone and a minor tone. In C major, the second note (D) will be 4 steps away. However, in A minor, where A is 6 steps below C, the fourth note (D) will be 9 steps above A, so 3 steps above C. So when switching from C major to A minor, one need to slightly change the note D. These discrepancies arise because, unlike 12-ET, 22-ET does not temper out the syntonic comma of 81/80, and in fact exaggerates its size by mapping it to one step. Exten ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
19-TET
In music, 19 Tone Equal Temperament, called 19 TET, 19 EDO ("Equal Division of the Octave"), or 19 ET, is the tempered scale derived by dividing the octave into 19 equal steps (equal frequency ratios). Each step represents a frequency ratio of , or 63.16 cents (). The fact that traditional western music maps unambiguously onto this scale (unless it presupposes 12-EDO enharmonic equivalences) makes it easier to perform such music in this tuning than in many other tunings. 19 EDO is the tuning of the syntonic temperament in which the tempered perfect fifth is equal to 694.737 cents, as shown in Figure 1 (look for the label "19 TET"). On an isomorphic keyboard, the fingering of music composed in 19 EDO is precisely the same as it is in any other syntonic tuning (such as 12 EDO), so long as the notes are "spelled properly" – that is, with no assumption that the sharp below matches the flat immediately above it (enharmo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
12-TET
Twelve-tone equal temperament (12-TET) is the musical system that divides the octave into 12 parts, all of which are equally tempered (equally spaced) on a logarithmic scale, with a ratio equal to the 12th root of 2 ( ≈ 1.05946). That resulting smallest interval, the width of an octave, is called a semitone or half step. Twelve-tone equal temperament is the most widespread system in music today. It has been the predominant tuning system of Western music, starting with classical music, since the 18th century, and Europe almost exclusively used approximations of it for millennia before that. It has also been used in other cultures. In modern times, 12-TET is usually tuned relative to a standard pitch of 440 Hz, called A440, meaning one note, A, is tuned to 440 hertz and all other notes are defined as some multiple of semitones apart from it, either higher or lower in frequency. The standard pitch has not always been 440 Hz. It has varied and generally risen over the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
72-et
In music, 72 equal temperament, called twelfth-tone, 72-TET, 72-EDO, or 72-ET, is the tempered scale derived by dividing the octave into twelfth-tones, or in other words 72 equal steps (equal frequency ratios). Each step represents a frequency ratio of , or cents, which divides the 100 cent "halftone" into 6 equal parts (100 ÷ = 6) and is thus a "twelfth-tone" (). Since 72 is divisible by 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72, 72-EDO includes all those equal temperaments. Since it contains so many temperaments, 72-EDO contains at the same time tempered semitones, third-tones, quartertones and sixth-tones, which makes it a very versatile temperament. This division of the octave has attracted much attention from tuning theorists, since on the one hand it subdivides the standard 12 equal temperament and on the other hand it accurately represents overtones up to the twelfth partial tone, and hence can be used for 11-limit music. It was theoreticized in the form of twelfth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |