|
Sensitivity And Specificity
''Sensitivity'' and ''specificity'' mathematically describe the accuracy of a test which reports the presence or absence of a condition. Individuals for which the condition is satisfied are considered "positive" and those for which it is not are considered "negative". *Sensitivity (true positive rate) refers to the probability of a positive test, conditioned on truly being positive. *Specificity (true negative rate) refers to the probability of a negative test, conditioned on truly being negative. If the true condition can not be known, a " gold standard test" is assumed to be correct. In a diagnostic test, sensitivity is a measure of how well a test can identify true positives and specificity is a measure of how well a test can identify true negatives. For all testing, both diagnostic and screening, there is usually a trade-off between sensitivity and specificity, such that higher sensitivities will mean lower specificities and vice versa. If the goal is to return the ratio at w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sensitivity And Specificity 1
Sensitivity may refer to: Science and technology Natural sciences * Sensitivity (physiology), the ability of an organism or organ to respond to external stimuli ** Sensory processing sensitivity in humans * Sensitivity and specificity, statistical measures of the performance of binary classification tests * Allergic sensitivity, the strength of a reaction to an allergen * The inverse of resistance (ecology), the ability of populations to remain stable when subject to disturbance Electronics * Sensitivity (electronics), the minimum magnitude of input signal required to produce a specified output signal ** Sensitivity of a transducer, the relationship between input and output power *** Sensitivity (electroacoustics) Mathematics * Sensitivity (control systems), variations in process dynamics and control systems * Sensitivity analysis, apportionment of the uncertainty in the output of a mathematical model among its inputs * Sensitivity and specificity, statistical measures of the per ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
False Alarm
A false alarm, also called a nuisance alarm, is the deceptive or erroneous report of an emergency, causing unnecessary panic and/or bringing resources (such as emergency services) to a place where they are not needed. False alarms may occur with residential burglary alarms, smoke detectors, industrial alarms, and in signal detection theory. False alarms have the potential to divert emergency responders away from legitimate emergencies, which could ultimately lead to loss of life. In some cases, repeated false alarms in a certain area may cause occupants to develop alarm fatigue and to start ignoring most alarms, knowing that each time it will probably be false. Intentionally falsely activating alarms in businesses and schools can lead to serious disciplinary actions, and criminal penalties such as fines and jail time. Overview The term “false alarm” refers to alarm systems in many different applications being triggered by something other than the expected trigger-event. Exa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brier Score
The Brier Score is a Scoring rule#StrictlyProperScoringRules, ''strictly proper score function'' or ''strictly proper scoring rule'' that measures the accuracy of probabilistic classification, probabilistic predictions. For unidimensional predictions, it is strictly equivalent to the mean squared error as applied to predicted probabilities. The Brier score is applicable to tasks in which predictions must assign probabilities to a set of mutually exclusive discrete outcomes or classes. The set of possible outcomes can be either binary or categorical in nature, and the probabilities assigned to this set of outcomes must sum to one (where each individual probability is in the range of 0 to 1). It was proposed by Glenn W. Brier in 1950. The Brier score can be thought of as a Loss function, cost function. More precisely, across all items i\in in a set of ''N'' predictions, the Brier score measures the mean squared difference between: * The predicted probability assigned to the possible ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Type I And Type II Errors
In statistical hypothesis testing, a type I error is the mistaken rejection of an actually true null hypothesis (also known as a "false positive" finding or conclusion; example: "an innocent person is convicted"), while a type II error is the failure to reject a null hypothesis that is actually false (also known as a "false negative" finding or conclusion; example: "a guilty person is not convicted"). Much of statistical theory revolves around the minimization of one or both of these errors, though the complete elimination of either is a statistical impossibility if the outcome is not determined by a known, observable causal process. By selecting a low threshold (cut-off) value and modifying the alpha (α) level, the quality of the hypothesis test can be increased. The knowledge of type I errors and type II errors is widely used in medical science, biometrics and computer science. Intuitively, type I errors can be thought of as errors of ''commission'', i.e. the researcher unluck ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Power
In statistics, the power of a binary hypothesis test is the probability that the test correctly rejects the null hypothesis (H_0) when a specific alternative hypothesis (H_1) is true. It is commonly denoted by 1-\beta, and represents the chances of a true positive detection conditional on the actual existence of an effect to detect. Statistical power ranges from 0 to 1, and as the power of a test increases, the probability \beta of making a type II error by wrongly failing to reject the null hypothesis decreases. Notation This article uses the following notation: * ''β'' = probability of a Type II error, known as a "false negative" * 1 − ''β'' = probability of a "true positive", i.e., correctly rejecting the null hypothesis. "1 − ''β''" is also known as the power of the test. * ''α'' = probability of a Type I error, known as a "false positive" * 1 − ''α'' = probability of a "true negative", i.e., correctly not rejecting the null hypothesis Description For a ty ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Hypothesis Testing
A statistical hypothesis test is a method of statistical inference used to decide whether the data at hand sufficiently support a particular hypothesis. Hypothesis testing allows us to make probabilistic statements about population parameters. History Early use While hypothesis testing was popularized early in the 20th century, early forms were used in the 1700s. The first use is credited to John Arbuthnot (1710), followed by Pierre-Simon Laplace (1770s), in analyzing the human sex ratio at birth; see . Modern origins and early controversy Modern significance testing is largely the product of Karl Pearson ( ''p''-value, Pearson's chi-squared test), William Sealy Gosset ( Student's t-distribution), and Ronald Fisher ("null hypothesis", analysis of variance, "significance test"), while hypothesis testing was developed by Jerzy Neyman and Egon Pearson (son of Karl). Ronald Fisher began his life in statistics as a Bayesian (Zabell 1992), but Fisher soon grew disenchanted with t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Mean
In mathematics, the harmonic mean is one of several kinds of average, and in particular, one of the Pythagorean means. It is sometimes appropriate for situations when the average rate is desired. The harmonic mean can be expressed as the reciprocal of the arithmetic mean of the reciprocals of the given set of observations. As a simple example, the harmonic mean of 1, 4, and 4 is : \left(\frac\right)^ = \frac = \frac = 2\,. Definition The harmonic mean ''H'' of the positive real numbers x_1, x_2, \ldots, x_n is defined to be :H = \frac = \frac = \left(\frac\right)^. The third formula in the above equation expresses the harmonic mean as the reciprocal of the arithmetic mean of the reciprocals. From the following formula: :H = \frac. it is more apparent that the harmonic mean is related to the arithmetic and geometric means. It is the reciprocal dual of the arithmetic mean for positive inputs: :1/H(1/x_1 \ldots 1/x_n) = A(x_1 \ldots x_n) The harmonic mean is a Schur-con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
F-score
In statistics, statistical analysis of binary classification, the F-score or F-measure is a measure of a test's Accuracy_and_precision#In_binary_classification, accuracy. It is calculated from the Precision (information retrieval), precision and Recall (information retrieval), recall of the test, where the precision is the number of true positive results divided by the number of all positive results, including those not identified correctly, and the recall is the number of true positive results divided by the number of all samples that should have been identified as positive. Precision is also known as positive predictive value, and recall is also known as Sensitivity_and_specificity, sensitivity in diagnostic binary classification. The F1 score is the harmonic mean of the precision and recall. The more generic F_\beta score applies additional weights, valuing one of precision or recall more than the other. The highest possible value of an F-score is 1.0, indicating perfect prec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Precision And Recall
In pattern recognition, information retrieval, object detection and classification (machine learning), precision and recall are performance metrics that apply to data retrieved from a collection, corpus or sample space. Precision (also called positive predictive value) is the fraction of relevant instances among the retrieved instances, while recall (also known as sensitivity) is the fraction of relevant instances that were retrieved. Both precision and recall are therefore based on relevance. Consider a computer program for recognizing dogs (the relevant element) in a digital photograph. Upon processing a picture which contains ten cats and twelve dogs, the program identifies eight dogs. Of the eight elements identified as dogs, only five actually are dogs (true positives), while the other three are cats (false positives). Seven dogs were missed (false negatives), and seven cats were correctly excluded (true negatives). The program's precision is then 5/8 (true positives / se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
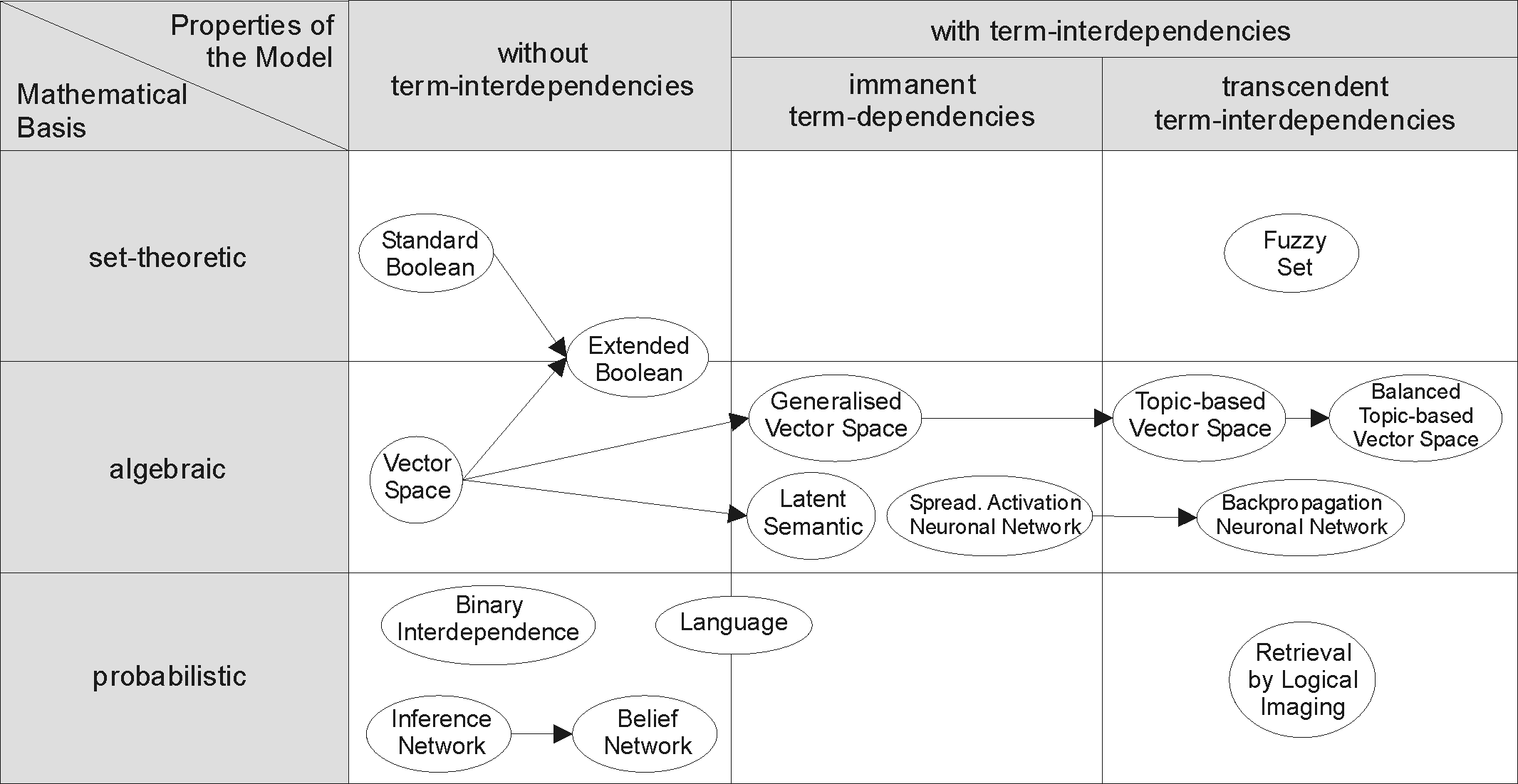
Information Retrieval
Information retrieval (IR) in computing and information science is the process of obtaining information system resources that are relevant to an information need from a collection of those resources. Searches can be based on full-text or other content-based indexing. Information retrieval is the science of searching for information in a document, searching for documents themselves, and also searching for the metadata that describes data, and for databases of texts, images or sounds. Automated information retrieval systems are used to reduce what has been called information overload. An IR system is a software system that provides access to books, journals and other documents; stores and manages those documents. Web search engines are the most visible IR applications. Overview An information retrieval process begins when a user or searcher enters a query into the system. Queries are formal statements of information needs, for example search strings in web search engines. In inf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Confidence Intervals
In frequentist statistics, a confidence interval (CI) is a range of estimates for an unknown parameter. A confidence interval is computed at a designated ''confidence level''; the 95% confidence level is most common, but other levels, such as 90% or 99%, are sometimes used. The confidence level represents the long-run proportion of corresponding CIs that contain the true value of the parameter. For example, out of all intervals computed at the 95% level, 95% of them should contain the parameter's true value. Factors affecting the width of the CI include the sample size, the variability in the sample, and the confidence level. All else being the same, a larger sample produces a narrower confidence interval, greater variability in the sample produces a wider confidence interval, and a higher confidence level produces a wider confidence interval. Definition Let be a random sample from a probability distribution with statistical parameter , which is a quantity to be estimated ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Proportion Confidence Interval
In statistics, a binomial proportion confidence interval is a confidence interval for the probability of success calculated from the outcome of a series of success–failure experiments (Bernoulli trials). In other words, a binomial proportion confidence interval is an interval estimate of a success probability ''p'' when only the number of experiments ''n'' and the number of successes ''nS'' are known. There are several formulas for a binomial confidence interval, but all of them rely on the assumption of a binomial distribution. In general, a binomial distribution applies when an experiment is repeated a fixed number of times, each trial of the experiment has two possible outcomes (success and failure), the probability of success is the same for each trial, and the trials are statistically independent. Because the binomial distribution is a discrete probability distribution (i.e., not continuous) and difficult to calculate for large numbers of trials, a variety of approximations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
