|
System Of Differential Equations
In mathematics, a system of differential equations is a finite set of differential equations. Such a system can be either linear or non-linear. Also, such a system can be either a system of ordinary differential equations or a system of partial differential equations. Linear system of differential equations Like any system of equations, a system of linear differential equations is said to be overdetermined if there are more equations than the unknowns. For an overdetermined system to have a solution, it needs to satisfy the compatibility conditions. For example, consider the system: :\frac = f_i, 1 \le i \le m. Then the necessary conditions for the system to have a solution are: :\frac - \frac = 0, 1 \le i, k \le m. See also: Cauchy problem and Ehrenpreis's fundamental principle. Non-linear system of differential equations Perhaps the most famous example of a non-linear system of differential equations is the Navier–Stokes equations. Unlike the linear case, the existe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, and the differential equation defines a relationship between the two. Such relations are common; therefore, differential equations play a prominent role in many disciplines including engineering, physics, economics, and biology. Mainly the study of differential equations consists of the study of their solutions (the set of functions that satisfy each equation), and of the properties of their solutions. Only the simplest differential equations are solvable by explicit formulas; however, many properties of solutions of a given differential equation may be determined without computing them exactly. Often when a closed-form expression for the solutions is not available, solutions may be approximated numerically using computers. The theory of d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
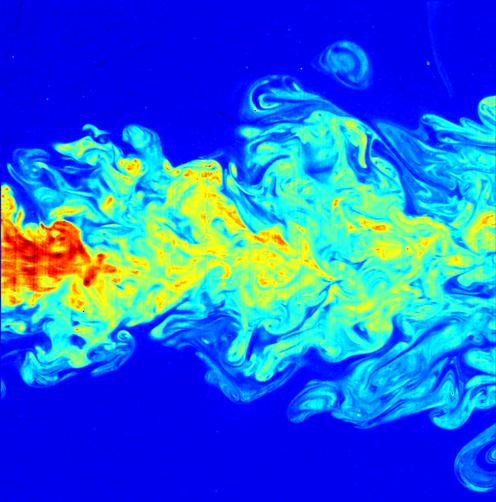
Navier–Stokes Existence And Smoothness
The Navier–Stokes existence and smoothness problem concerns the mathematical properties of solutions to the Navier–Stokes equations, a system of partial differential equations that describe the motion of a fluid in space. Solutions to the Navier–Stokes equations are used in many practical applications. However, theoretical understanding of the solutions to these equations is incomplete. In particular, solutions of the Navier–Stokes equations often include turbulence, which remains one of the greatest unsolved problems in physics, despite its immense importance in science and engineering. Even more basic (and seemingly intuitive) properties of the solutions to Navier–Stokes have never been proven. For the three-dimensional system of equations, and given some initial conditions, mathematicians have neither proved that smooth solutions always exist, nor found any counter-examples. This is called the ''Navier–Stokes existence and smoothness'' problem. Since underst ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Equations
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, and the differential equation defines a relationship between the two. Such relations are common; therefore, differential equations play a prominent role in many disciplines including engineering, physics, economics, and biology. Mainly the study of differential equations consists of the study of their solutions (the set of functions that satisfy each equation), and of the properties of their solutions. Only the simplest differential equations are solvable by explicit formulas; however, many properties of solutions of a given differential equation may be determined without computing them exactly. Often when a closed-form expression for the solutions is not available, solutions may be approximated numerically using computers. The theory of d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartan–Kuranishi Prolongation Theorem
Given an exterior differential system defined on a manifold ''M'', the Cartan–Kuranishi prolongation theorem says that after a finite number of ''prolongations'' the system is either ''in involution'' (admits at least one 'large' integral manifold), or is impossible. History The theorem is named after Élie Cartan and Masatake Kuranishi. Applications This theorem is used in infinite-dimensional Lie theory In mathematics, the mathematician Sophus Lie ( ) initiated lines of study involving integration of differential equations, transformation groups, and contact of spheres that have come to be called Lie theory. For instance, the latter subject is L .... See also * Cartan-Kähler theorem References * M. Kuranishi, ''On É. Cartan's prolongation theorem of exterior differential systems'', Amer. J. Math., vol. 79, 1957, p. 1–47 * {{DEFAULTSORT:Cartan-Kuranishi prolongation theorem Partial differential equations Theorems in analysis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral Geometry
In mathematics, integral geometry is the theory of measures on a geometrical space invariant under the symmetry group of that space. In more recent times, the meaning has been broadened to include a view of invariant (or equivariant) transformations from the space of functions on one geometrical space to the space of functions on another geometrical space. Such transformations often take the form of integral transforms such as the Radon transform and its generalizations. Classical context Integral geometry as such first emerged as an attempt to refine certain statements of geometric probability theory. The early work of Luis Santaló and Wilhelm Blaschke was in this connection. It follows from the classic theorem of Crofton expressing the length of a plane curve as an expectation of the number of intersections with a random line. Here the word 'random' must be interpreted as subject to correct symmetry considerations. There is a sample space of lines, one on which the affin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
:Category:differential Systems
A differential system is a means of studying a system of partial differential equations using geometric ideas such as differential forms In mathematics, differential forms provide a unified approach to define integrands over curves, surfaces, solids, and higher-dimensional manifolds. The modern notion of differential forms was pioneered by Élie Cartan. It has many applications, ... and vector fields. Partial differential equations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integrability Conditions For Differential Systems
In mathematics, certain systems of partial differential equations are usefully formulated, from the point of view of their underlying geometric and algebraic structure, in terms of a system of differential forms. The idea is to take advantage of the way a differential form ''restricts'' to a submanifold, and the fact that this restriction is compatible with the exterior derivative. This is one possible approach to certain over-determined systems, for example, including Lax pairs of integrable systems. A Pfaffian system is specified by 1-forms alone, but the theory includes other types of example of differential system. To elaborate, a Pfaffian system is a set of 1-forms on a smooth manifold (which one sets equal to 0 to find ''solutions'' to the system). Given a collection of differential 1-forms \textstyle\alpha_i, i=1,2,\dots, k on an \textstyle n-dimensional manifold M, an integral manifold is an immersed (not necessarily embedded) submanifold whose tangent space at every point ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
H-principle
In mathematics, the homotopy principle (or h-principle) is a very general way to solve partial differential equations (PDEs), and more generally partial differential relations (PDRs). The h-principle is good for underdetermined PDEs or PDRs, such as the immersion problem, isometric immersion problem, fluid dynamics, and other areas. The theory was started by Yakov Eliashberg, Mikhail Gromov and Anthony V. Phillips. It was based on earlier results that reduced partial differential relations to homotopy, particularly for immersions. The first evidence of h-principle appeared in the Whitney–Graustein theorem. This was followed by the Nash–Kuiper isometric ''C''1 embedding theorem and the Smale–Hirsch immersion theorem. Rough idea Assume we want to find a function ''ƒ'' on R''m'' which satisfies a partial differential equation of degree ''k'', in co-ordinates (u_1,u_2,\dots,u_m). One can rewrite it as :\Psi(u_1,u_2,\dots,u_m, J^k_f)=0 where J^k_f stands for all parti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Navier–Stokes Equations
In physics, the Navier–Stokes equations ( ) are partial differential equations which describe the motion of viscous fluid substances, named after French engineer and physicist Claude-Louis Navier and Anglo-Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes). The Navier–Stokes equations mathematically express conservation of momentum and conservation of mass for Newtonian fluids. They are sometimes accompanied by an equation of state relating pressure, temperature and density. They arise from applying Isaac Newton's second law to fluid motion, together with the assumption that the stress in the fluid is the sum of a diffusing viscous term (proportional to the gradient of velocity) and a pressure term—hence describing ''viscous flow''. The difference between them and the closely related Euler equations is that Navier–Stokes equations take ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Differential Equations
In mathematics, a linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form :a_0(x)y + a_1(x)y' + a_2(x)y'' \cdots + a_n(x)y^ = b(x) where and are arbitrary differentiable functions that do not need to be linear, and are the successive derivatives of an unknown function of the variable . Such an equation is an ordinary differential equation (ODE). A ''linear differential equation'' may also be a linear partial differential equation (PDE), if the unknown function depends on several variables, and the derivatives that appear in the equation are partial derivatives. A linear differential equation or a system of linear equations such that the associated homogeneous equations have constant coefficients may be solved by quadrature, which means that the solutions may be expressed in terms of integrals. This is also true for a linear equation of order one, with non-con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ehrenpreis's Fundamental Principle
In mathematical analysis, Ehrenpreis's fundamental principle, introduced by Leon Ehrenpreis Eliezer 'Leon' Ehrenpreis (May 22, 1930 – August 16, 2010, Brooklyn) was a mathematician at Temple University who proved the Malgrange–Ehrenpreis theorem, the fundamental theorem about differential operators with constant coefficients. He pre ..., states: :Every solution of a system (in general, overdetermined) of homogeneous partial differential equations with constant coefficients can be represented as the integral with respect to an appropriate Radon measure over the complex “ characteristic variety” of the system. References Mathematical analysis {{analysis-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy Problem
A Cauchy problem in mathematics asks for the solution of a partial differential equation that satisfies certain conditions that are given on a hypersurface in the domain. A Cauchy problem can be an initial value problem or a boundary value problem (for this case see also Cauchy boundary condition). It is named after Augustin-Louis Cauchy. Formal statement For a partial differential equation defined on R''n+1'' and a smooth manifold ''S'' ⊂ R''n+1'' of dimension ''n'' (''S'' is called the Cauchy surface), the Cauchy problem consists of finding the unknown functions u_1,\dots,u_N of the differential equation with respect to the independent variables t,x_1,\dots,x_n that satisfiesPetrovskii, I. G. (1954). Lectures on partial differential equations. Interscience Publishers, Inc, Translated by A. Shenitzer, (Dover publications, 1991) \begin&\frac = F_i\left(t,x_1,\dots,x_n,u_1,\dots,u_N,\dots,\frac,\dots\right) \\ &\text i,j = 1,2,\dots,N;\, k_0+k_1+\dots+k_n=k\leq n_j;\, k_0 [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
