|
Sum
Sum most commonly means the total of two or more numbers added together; see addition. Sum can also refer to: Mathematics * Sum (category theory), the generic concept of summation in mathematics * Sum, the result of summation, the addition of a sequence of numbers * 3SUM, a term from computational complexity theory * Band sum, a way of connecting mathematical knots * Connected sum, a way of gluing manifolds * Digit sum, in number theory * Direct sum, a combination of algebraic objects ** Direct sum of groups ** Direct sum of modules ** Direct sum of permutations ** Direct sum of topological groups * Einstein summation, a way of contracting tensor indices * Empty sum, a sum with no terms * Indefinite sum, the inverse of a finite difference * Kronecker sum, an operation considered a kind of addition for matrices * Matrix addition, in linear algebra * Minkowski addition, a sum of two subsets of a vector space * Power sum symmetric polynomial, in commutative algebra * Pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Summation
In mathematics, summation is the addition of a sequence of numbers, called ''addends'' or ''summands''; the result is their ''sum'' or ''total''. Beside numbers, other types of values can be summed as well: functions, vectors, matrices, polynomials and, in general, elements of any type of mathematical objects on which an operation denoted "+" is defined. Summations of infinite sequences are called series. They involve the concept of limit, and are not considered in this article. The summation of an explicit sequence is denoted as a succession of additions. For example, summation of is denoted , and results in 9, that is, . Because addition is associative and commutative, there is no need for parentheses, and the result is the same irrespective of the order of the summands. Summation of a sequence of only one summand results in the summand itself. Summation of an empty sequence (a sequence with no elements), by convention, results in 0. Very often, the elements of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indefinite Sum
In discrete calculus the indefinite sum operator (also known as the antidifference operator), denoted by \sum _x or \Delta^ , is the linear operator, inverse of the forward difference operator \Delta . It relates to the forward difference operator as the indefinite integral relates to the derivative. Thus :\Delta \sum_x f(x) = f(x) \, . More explicitly, if \sum_x f(x) = F(x) , then :F(x+1) - F(x) = f(x) \, . If ''F''(''x'') is a solution of this functional equation for a given ''f''(''x''), then so is ''F''(''x'')+''C''(''x'') for any periodic function ''C''(''x'') with period 1. Therefore, each indefinite sum actually represents a family of functions. However, due to the Carlson's theorem, the solution equal to its Newton series expansion is unique up to an additive constant ''C''. This unique solution can be represented by formal power series form of the antidifference operator: \Delta^=\frac1. Fundamental theorem of discrete calculus Indefinite sums can be used to calcu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann Sum
In mathematics, a Riemann sum is a certain kind of approximation of an integral by a finite sum. It is named after nineteenth century German mathematician Bernhard Riemann. One very common application is in numerical integration, i.e., approximating the area of functions or lines on a graph, where it is also known as the rectangle rule. It can also be applied for approximating the length of curves and other approximations. The sum is calculated by partitioning the region into shapes (rectangles, trapezoids, parabolas, or cubics—sometimes infinitesimally small) that together form a region that is similar to the region being measured, then calculating the area for each of these shapes, and finally adding all of these small areas together. This approach can be used to find a numerical approximation for a definite integral even if the fundamental theorem of calculus does not make it easy to find a closed-form solution. Because the region by the small shapes is usually not ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
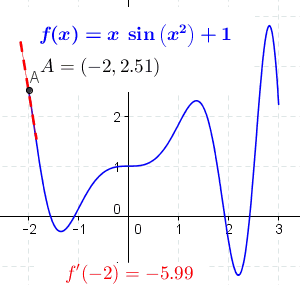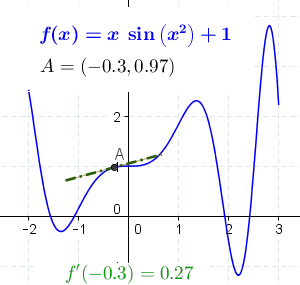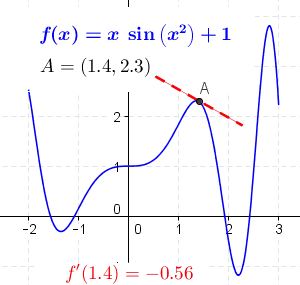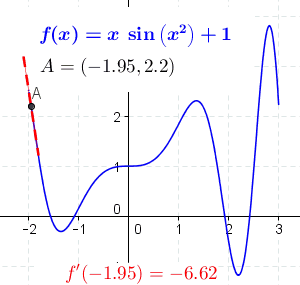
Sum Rule In Differentiation
This article is a summary of differentiation rules, that is, rules for computing the derivative of a function in calculus. Elementary rules of differentiation Unless otherwise stated, all functions are functions of real numbers (\mathbb) that return real values, although, more generally, the formulas below apply wherever they are well defined, including the case of complex numbers (\mathbb). Constant term rule For any value of c, where c \in \mathbb, if f(x) is the constant function given by f(x) = c, then \frac = 0. Proof Let c \in \mathbb and f(x) = c. By the definition of the derivative: \begin f'(x) &= \lim_\frac \\ &= \lim_ \frac \\ &= \lim_ \frac \\ &= \lim_ 0 \\ &= 0. \end This computation shows that the derivative of any constant function is 0. Intuitive (geometric) explanation The derivative of the function at a point is the slope of the line tangent to the curve at the point. The slope of the constant function is 0, because the tangent line to the constant function ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Direct Sum Of Modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The direct sum of modules is the smallest module which contains the given modules as submodules with no "unnecessary" constraints, making it an example of a coproduct. Contrast with the direct product, which is the dual notion. The most familiar examples of this construction occur when considering vector spaces (modules over a field) and abelian groups (modules over the ring Z of integers). The construction may also be extended to cover Banach spaces and Hilbert spaces. See the article decomposition of a module for a way to write a module as a direct sum of submodules. Construction for vector spaces and abelian groups We give the construction first in these two cases, under the assumption that we have only two objects. Then we generalize to an arbitrary family of arbitrary modules. The key elements of the general construction are more clearly identified ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Space
In mathematics and physics, a vector space (also called a linear space) is a set (mathematics), set whose elements, often called vector (mathematics and physics), ''vectors'', can be added together and multiplied ("scaled") by numbers called scalar (mathematics), ''scalars''. The operations of vector addition and scalar multiplication must satisfy certain requirements, called ''vector axioms''. Real vector spaces and complex vector spaces are kinds of vector spaces based on different kinds of scalars: real numbers and complex numbers. Scalars can also be, more generally, elements of any field (mathematics), field. Vector spaces generalize Euclidean vectors, which allow modeling of Physical quantity, physical quantities (such as forces and velocity) that have not only a Magnitude (mathematics), magnitude, but also a Orientation (geometry), direction. The concept of vector spaces is fundamental for linear algebra, together with the concept of matrix (mathematics), matrices, which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sum Rule In Quantum Mechanics
In quantum mechanics, a sum rule is a formula for transitions between energy levels, in which the sum of the transition strengths is expressed in a simple form. Sum rules are used to describe the properties of many physical systems, including solids, atoms, atomic nuclei, and nuclear constituents such as protons and neutrons. The sum rules are derived from general principles, and are useful in situations where the behavior of individual energy levels is too complex to be described by a precise quantum-mechanical theory. In general, sum rules are derived by using Heisenberg's quantum-mechanical algebra to construct operator equalities, which are then applied to the particles or energy levels of a system. Derivation of sum rules Assume that the Hamiltonian Hamiltonian may refer to: * Hamiltonian mechanics, a function that represents the total energy of a system * Hamiltonian (quantum mechanics), an operator corresponding to the total energy of that system ** Dyall Hamiltonian, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Einstein Summation
In mathematics, especially the usage of linear algebra in mathematical physics and differential geometry, Einstein notation (also known as the Einstein summation convention or Einstein summation notation) is a notational convention that implies summation over a set of indexed terms in a formula, thus achieving brevity. As part of mathematics it is a notational subset of Ricci calculus; however, it is often used in physics applications that do not distinguish between tangent and cotangent spaces. It was introduced to physics by Albert Einstein in 1916. Introduction Statement of convention According to this convention, when an index variable appears twice in a single term and is not otherwise defined (see Free and bound variables), it implies summation of that term over all the values of the index. So where the indices can range over the set , y = \sum_^3 x^i e_i = x^1 e_1 + x^2 e_2 + x^3 e_3 is simplified by the convention to: y = x^i e_i The upper indices are not expon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Sum Symmetric Polynomial
In mathematics, specifically in commutative algebra, the power sum symmetric polynomials are a type of basic building block for symmetric polynomials, in the sense that every symmetric polynomial with rational coefficients can be expressed as a sum and difference of products of power sum symmetric polynomials with rational coefficients. However, not every symmetric polynomial with integral coefficients is generated by integral combinations of products of power-sum polynomials: they are a generating set over the ''rationals,'' but not over the ''integers.'' Definition The power sum symmetric polynomial of degree ''k'' in n variables ''x''1, ..., ''x''''n'', written ''p''''k'' for ''k'' = 0, 1, 2, ..., is the sum of all ''k''th powers of the variables. Formally, : p_k (x_1, x_2, \dots,x_n) = \sum_^n x_i^k \, . The first few of these polynomials are :p_0 (x_1, x_2, \dots,x_n) = 1 + 1 + \cdots + 1 = n \, , :p_1 (x_1, x_2, \dots,x_n) = x_1 + x_2 + \cdots + x_n \, , :p_2 (x_1, x_2, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Digit Sum
In mathematics, the digit sum of a natural number in a given radix, number base is the sum of all its numerical digit, digits. For example, the digit sum of the decimal number 9045 would be 9 + 0 + 4 + 5 = 18. Definition Let n be a natural number. We define the digit sum for base b > 1, F_b : \mathbb \rightarrow \mathbb to be the following: :F_b(n) = \sum_^ d_i where k = \lfloor \log_ \rfloor is one less than the number of digits in the number in base b, and :d_i = \frac is the value of each digit of the number. For example, in base 10, the digit sum of 84001 is F_(84001) = 8 + 4 + 0 + 0 + 1 = 13. For any two bases 2 \leq b_1 < b_2 and for sufficiently large natural numbers :. The sum of the base 10 digits of the integers 0, 1, 2, ... is given by in the On-Line Encyclopedia of Integer Sequences. use the generating function of this integer sequence (and of the analogous sequence for binary ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prefix Sum
In computer science, the prefix sum, cumulative sum, inclusive scan, or simply scan of a sequence of numbers is a second sequence of numbers , the summation, sums of Prefix (computer science), prefixes (running totals) of the input sequence: : : : :... For instance, the prefix sums of the natural numbers are the triangular numbers: : Prefix sums are trivial to compute in sequential models of computation, by using the formula to compute each output value in sequence order. However, despite their ease of computation, prefix sums are a useful primitive in certain algorithms such as counting sort,. and they form the basis of the scan higher-order function in functional programming languages. Prefix sums have also been much studied in parallel algorithms, both as a test problem to be solved and as a useful primitive to be used as a subroutine in other parallel algorithms.. Abstractly, a prefix sum requires only a semigroup, binary associative operator ⊕, making it useful for many a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rule Of Sum
In combinatorics, the addition principle or rule of sum is a basic counting principle. Stated simply, it is the intuitive idea that if we have ''A'' number of ways of doing something and ''B'' number of ways of doing another thing and we can not do both at the same time, then there are A + B ways to choose one of the actions. In mathematical terms, the addition principle states that, for disjoint sets ''A'' and ''B'', we have , A\cup B, = , A, + , B, , provided that the intersection of the sets is without any elements. The rule of sum is a fact about set theory, as can be seen with the previously mentioned equation for the union of disjoint sets A and B being equal to , A, + , B, . The addition principle can be extended to several sets. If S_1, S_2,\ldots, S_n are pairwise disjoint sets, then we have:, S_1, +, S_2, +\cdots+, S_, = , S_1 \cup S_2 \cup \cdots \cup S_n, . This statement can be proven from the addition principle by induction on ''n''. Simple example A p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |