|
Stokes Parameters
The Stokes parameters are a set of values that describe the polarization state of electromagnetic radiation. They were defined by George Gabriel Stokes in 1852, as a mathematically convenient alternative to the more common description of incoherent or partially polarized radiation in terms of its total intensity (''I''), (fractional) degree of polarization (''p''), and the shape parameters of the polarization ellipse. The effect of an optical system on the polarization of light can be determined by constructing the Stokes vector for the input light and applying Mueller calculus, to obtain the Stokes vector of the light leaving the system. The original Stokes paper was discovered independently by Francis Perrin in 1942 and by Subrahamanyan Chandrasekhar in 1947, who named it as the Stokes parameters. Definitions The relationship of the Stokes parameters ''S''0, ''S''1, ''S''2, ''S''3 to intensity and polarization ellipse parameters is shown in the equations below and the fig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jones Vector
In optics, polarized light can be described using the Jones calculus, discovered by R. C. Jones in 1941. Polarized light is represented by a Jones vector, and linear optical elements are represented by ''Jones matrices''. When light crosses an optical element the resulting polarization of the emerging light is found by taking the product of the Jones matrix of the optical element and the Jones vector of the incident light. Note that Jones calculus is only applicable to light that is already fully polarized. Light which is randomly polarized, partially polarized, or incoherent must be treated using Mueller calculus. Jones vector The Jones vector describes the polarization of light in free space or another homogeneous isotropic non-attenuating medium, where the light can be properly described as transverse waves. Suppose that a monochromatic plane wave of light is travelling in the positive ''z''-direction, with angular frequency ''ω'' and wave vector k = (0,0,''k''), where the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semi-minor Axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both focus (geometry), foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major wikt:semiaxis, semiaxis) is the longest semidiameter or one half of the major axis, and thus runs from the centre, through a focus (geometry), focus, and to the perimeter. The semi-minor axis (minor semiaxis) of an ellipse or hyperbola is a line segment that is at right angles with the semi-major axis and has one end at the center of the conic section. For the special case of a circle, the lengths of the semi-axes are both equal to the radius of the circle. The length of the semi-major axis of an ellipse is related to the semi-minor axis's length through the eccentricity (mathematics), eccentricity and the semi-latus rectum \ell, as follows: The semi-major axis of a hyperbola is, depending on the convention, plus or minus one half of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semi-major Axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the longest semidiameter or one half of the major axis, and thus runs from the centre, through a focus, and to the perimeter. The semi-minor axis (minor semiaxis) of an ellipse or hyperbola is a line segment that is at right angles with the semi-major axis and has one end at the center of the conic section. For the special case of a circle, the lengths of the semi-axes are both equal to the radius of the circle. The length of the semi-major axis of an ellipse is related to the semi-minor axis's length through the eccentricity and the semi-latus rectum \ell, as follows: The semi-major axis of a hyperbola is, depending on the convention, plus or minus one half of the distance between the two branches. Thus it is the distance from the center ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity (mathematics), eccentricity e, a number ranging from e = 0 (the Limiting case (mathematics), limiting case of a circle) to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola). An ellipse has a simple algebraic solution for its area, but only approximations for its perimeter (also known as circumference), for which integration is required to obtain an exact solution. Analytic geometry, Analytically, the equation of a standard ellipse centered at the origin with width 2a and height 2b is: : \frac+\frac = 1 . Assuming a \ge b, the foci are (\pm c, 0) for c = \sqrt. The standard parametric e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degeneracy (mathematics)
In mathematics, a degenerate case is a limiting case of a class of objects which appears to be qualitatively different from (and usually simpler than) the rest of the class, and the term degeneracy is the condition of being a degenerate case. The definitions of many classes of composite or structured objects often implicitly include inequalities. For example, the angles and the side lengths of a triangle are supposed to be positive. The limiting cases, where one or several of these inequalities become equalities, are degeneracies. In the case of triangles, one has a ''degenerate triangle'' if at least one side length or angle is zero. Equivalently, it becomes a "line segment". Often, the degenerate cases are the exceptional cases where changes to the usual dimension or the cardinality of the object (or of some part of it) occur. For example, a triangle is an object of dimension two, and a degenerate triangle is contained in a line, which makes its dimension one. This is similar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
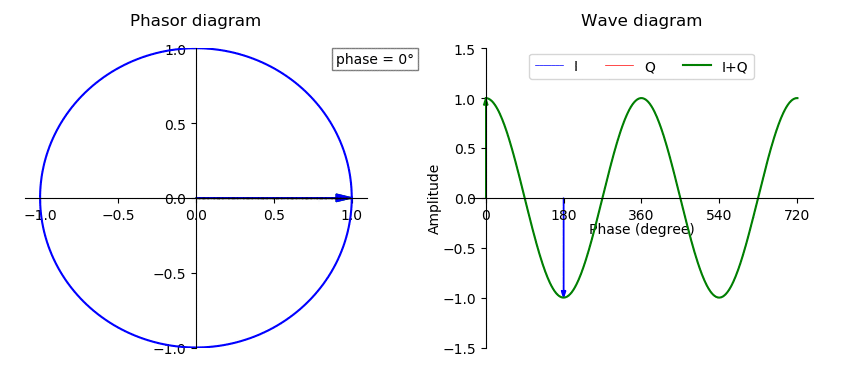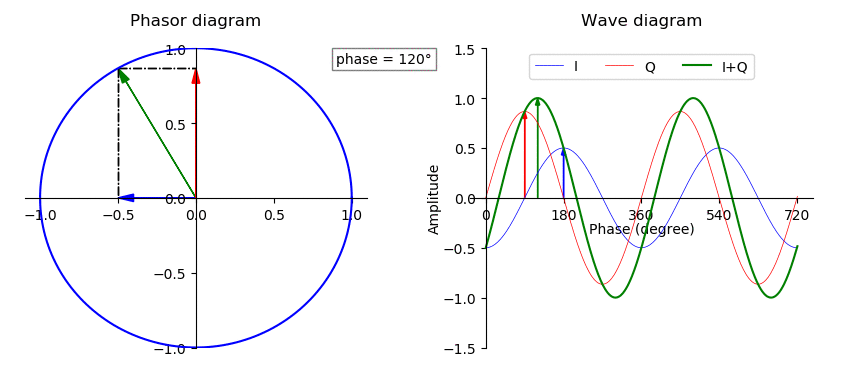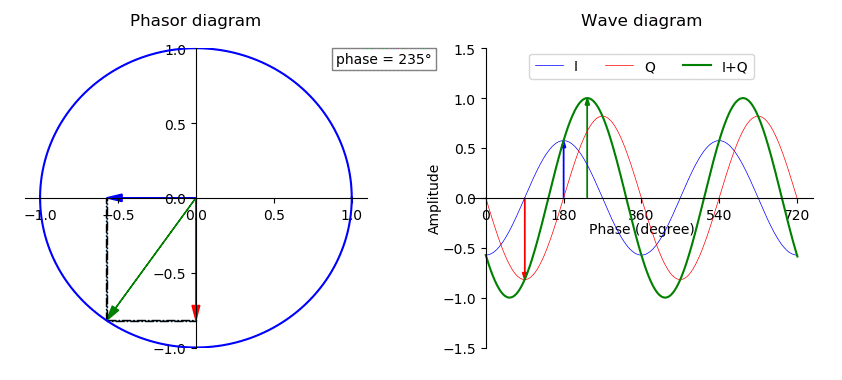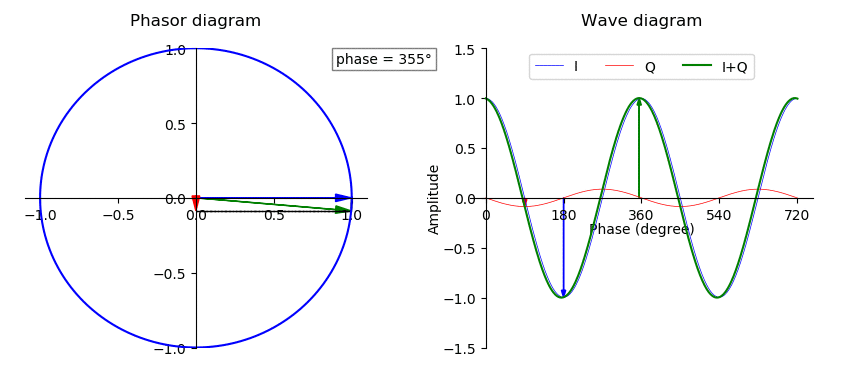
Phase (waves)
In physics and mathematics, the phase of a periodic function F of some real variable t (such as time) is an angle-like quantity representing the fraction of the cycle covered up to t. It is denoted \phi(t) and expressed in such a scale that it varies by one full turn as the variable t goes through each period (and F(t) goes through each complete cycle). It may be measured in any angular unit such as degrees or radians, thus increasing by 360° or 2\pi as the variable t completes a full period. This convention is especially appropriate for a sinusoidal function, since its value at any argument t then can be expressed as \phi(t), the sine of the phase, multiplied by some factor (the amplitude of the sinusoid). (The cosine may be used instead of sine, depending on where one considers each period to start.) Usually, whole turns are ignored when expressing the phase; so that \phi(t) is also a periodic function, with the same period as F, that repeatedly scans the same range of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Basis (linear Algebra)
In mathematics, a set of vectors in a vector space is called a basis if every element of may be written in a unique way as a finite linear combination of elements of . The coefficients of this linear combination are referred to as components or coordinates of the vector with respect to . The elements of a basis are called . Equivalently, a set is a basis if its elements are linearly independent and every element of is a linear combination of elements of . In other words, a basis is a linearly independent spanning set. A vector space can have several bases; however all the bases have the same number of elements, called the ''dimension'' of the vector space. This article deals mainly with finite-dimensional vector spaces. However, many of the principles are also valid for infinite-dimensional vector spaces. Definition A basis of a vector space over a field (such as the real numbers or the complex numbers ) is a linearly independent subset of that spans . This me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electric Field
An electric field (sometimes E-field) is the physical field that surrounds electrically charged particles and exerts force on all other charged particles in the field, either attracting or repelling them. It also refers to the physical field for a system of charged particles. Electric fields originate from electric charges and time-varying electric currents. Electric fields and magnetic fields are both manifestations of the electromagnetic field, one of the four fundamental interactions (also called forces) of nature. Electric fields are important in many areas of physics, and are exploited in electrical technology. In atomic physics and chemistry, for instance, the electric field is the attractive force holding the atomic nucleus and electrons together in atoms. It is also the force responsible for chemical bonding between atoms that result in molecules. The electric field is defined as a vector field that associates to each point in space the electrostatic ( Coulomb) for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Amplitude
Complex commonly refers to: * Complexity, the behaviour of a system whose components interact in multiple ways so possible interactions are difficult to describe ** Complex system, a system composed of many components which may interact with each other * Complex (psychology), a core pattern of emotions etc. in the personal unconscious organized around a common theme such as power or status Complex may also refer to: Arts, entertainment and media * Complex (English band), formed in 1968, and their 1971 album ''Complex'' * Complex (band), a Japanese rock band * ''Complex'' (album), by Montaigne, 2019, and its title track * ''Complex'' (EP), by Rifle Sport, 1985 * "Complex" (song), by Gary Numan, 1979 * Complex Networks, publisher of magazine ''Complex'', now online Biology * Protein–ligand complex, a complex of a protein bound with a ligand * Exosome complex, a multi-protein intracellular complex * Protein complex, a group of two or more associated polypeptide chains * Specie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Propagation Vector
In physics, a wave vector (or wavevector) is a vector used in describing a wave, with a typical unit being cycle per metre. It has a magnitude and direction. Its magnitude is the wavenumber of the wave (inversely proportional to the wavelength), and its direction is perpendicular to the wavefront. In isotropic media, this is also the direction of wave propagation. A closely related vector is the angular wave vector (or angular wavevector), with a typical unit being radian per metre. The wave vector and angular wave vector are related by a fixed constant of proportionality, 2π radians per cycle. It is common in several fields of physics to refer to the angular wave vector simply as the ''wave vector'', in contrast to, for example, crystallography. It is also common to use the symbol ''k'' for whichever is in use. In the context of special relativity, ''wave vector'' can refer to a four-vector, in which the (angular) wave vector and (angular) frequency are combined. De ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plane Wave
In physics, a plane wave is a special case of wave or field: a physical quantity whose value, at any moment, is constant through any plane that is perpendicular to a fixed direction in space. For any position \vec x in space and any time t, the value of such a field can be written as :F(\vec x,t) = G(\vec x \cdot \vec n, t), where \vec n is a unit-length vector, and G(d,t) is a function that gives the field's value as dependent on only two real parameters: the time t, and the scalar-valued displacement d = \vec x \cdot \vec n of the point \vec x along the direction \vec n. The displacement is constant over each plane perpendicular to \vec n. The values of the field F may be scalars, vectors, or any other physical or mathematical quantity. They can be complex numbers, as in a complex exponential plane wave. When the values of F are vectors, the wave is said to be a longitudinal wave if the vectors are always collinear with the vector \vec n, and a transverse wave if they ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
