|
Steiner's Conic Problem
In enumerative geometry, Steiner's conic problem is the problem of finding the number of smooth conics tangent to five given conics in the plane in general position. If the problem is considered in the complex projective plane CP2, the correct solution is 3264 (). The problem is named after Jakob Steiner who first posed it and who gave an incorrect solution in 1848. History claimed that the number of conics tangent to 5 given conics in general position is 7776 = 65, but later realized this was wrong. The correct number 3264 was found in about 1859 by Ernest de Jonquières who did not publish because of Steiner's reputation, and by using his theory of characteristics, and by Berner in 1865. However these results, like many others in classical intersection theory, do not seem to have been given complete proofs until the work of Fulton and Macpherson in about 1978. Formulation and solution The space of (possibly degenerate) conics in the complex projective plane CP2 can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Enumerative Geometry
In mathematics, enumerative geometry is the branch of algebraic geometry concerned with counting numbers of solutions to geometric questions, mainly by means of intersection theory. History The problem of Apollonius is one of the earliest examples of enumerative geometry. This problem asks for the number and construction of circles that are tangent to three given circles, points or lines. In general, the problem for three given circles has eight solutions, which can be seen as 23, each tangency condition imposing a quadratic condition on the space of circles. However, for special arrangements of the given circles, the number of solutions may also be any integer from 0 (no solutions) to six; there is no arrangement for which there are seven solutions to Apollonius' problem. Key tools A number of tools, ranging from the elementary to the more advanced, include: * Dimension counting * Bézout's theorem * Schubert calculus, and more generally characteristic classes in coh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
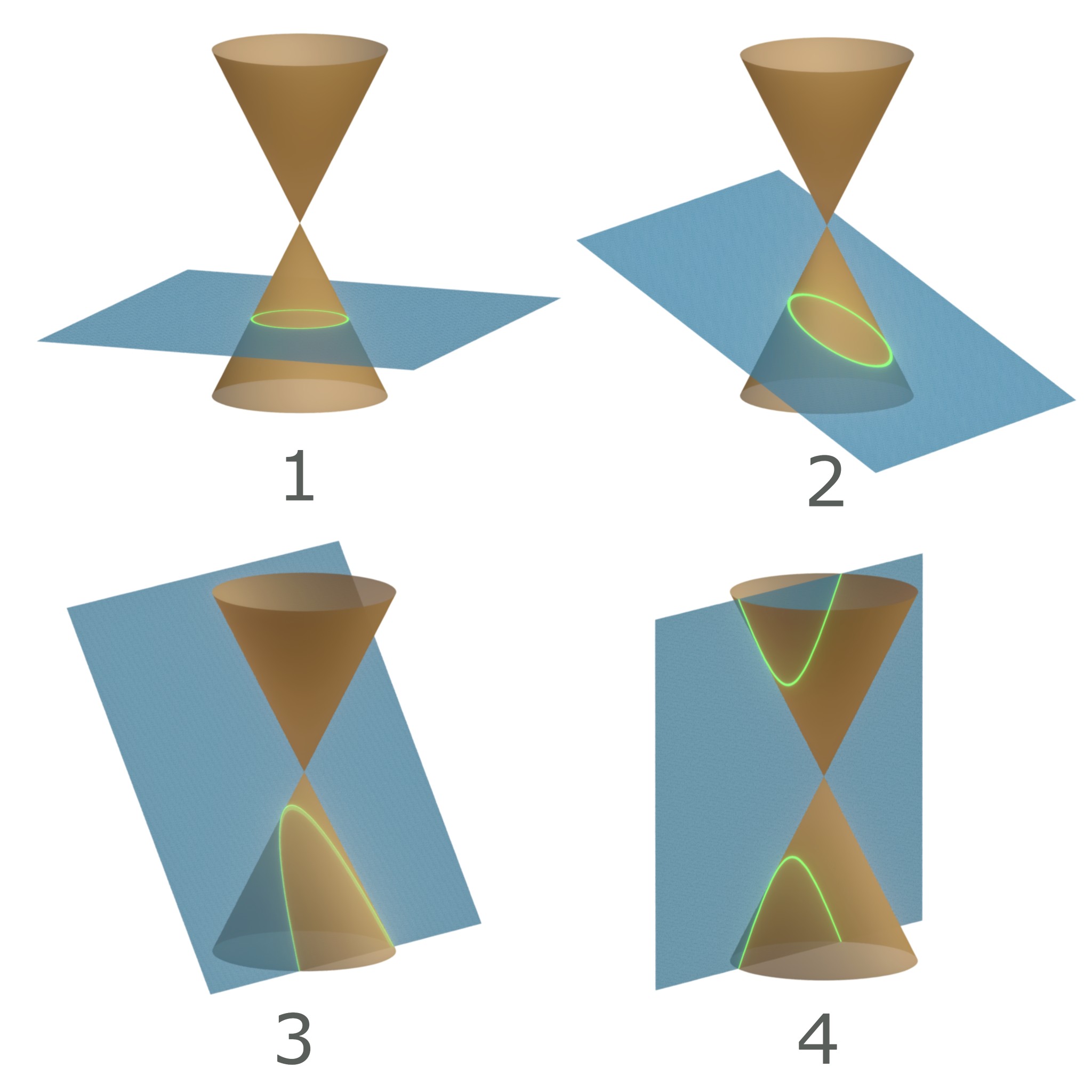
Conic Section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a '' focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the '' eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebrai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
General Position
In algebraic geometry and computational geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the ''general case'' situation, as opposed to some more special or coincidental cases that are possible, which is referred to as special position. Its precise meaning differs in different settings. For example, generically, two lines in the plane intersect in a single point (they are not parallel or coincident). One also says "two generic lines intersect in a point", which is formalized by the notion of a generic point. Similarly, three generic points in the plane are not collinear; if three points are collinear (even stronger, if two coincide), this is a degenerate case. This notion is important in mathematics and its applications, because degenerate cases may require an exceptional treatment; for example, when stating general theorems or giving precise statements thereof, and when writing computer programs (see '' generic co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Projective Plane
In mathematics, the complex projective plane, usually denoted P2(C), is the two-dimensional complex projective space. It is a complex manifold of complex dimension 2, described by three complex coordinates :(Z_1,Z_2,Z_3) \in \mathbf^3,\qquad (Z_1,Z_2,Z_3)\neq (0,0,0) where, however, the triples differing by an overall rescaling are identified: :(Z_1,Z_2,Z_3) \equiv (\lambda Z_1,\lambda Z_2, \lambda Z_3);\quad \lambda\in \mathbf,\qquad \lambda \neq 0. That is, these are homogeneous coordinates in the traditional sense of projective geometry. Topology The Betti numbers of the complex projective plane are :1, 0, 1, 0, 1, 0, 0, ..... The middle dimension 2 is accounted for by the homology class of the complex projective line, or Riemann sphere, lying in the plane. The nontrivial homotopy groups of the complex projective plane are \pi_2=\pi_5=\mathbb. The fundamental group is trivial and all other higher homotopy groups are those of the 5-sphere, i.e. torsion. Algebraic geomet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jakob Steiner
Jakob Steiner (18 March 1796 – 1 April 1863) was a Swiss mathematician who worked primarily in geometry. Life Steiner was born in the village of Utzenstorf, Canton of Bern. At 18, he became a pupil of Heinrich Pestalozzi and afterwards studied at Heidelberg. Then, he went to Berlin, earning a livelihood there, as in Heidelberg, by tutoring. Here he became acquainted with A. L. Crelle, who, encouraged by his ability and by that of Niels Henrik Abel, then also staying at Berlin, founded his famous ''Journal'' (1826). After Steiner's publication (1832) of his ''Systematische Entwickelungen'' he received, through Carl Gustav Jacob Jacobi, who was then professor at Königsberg University, and earned an honorary degree there; and through the influence of Jacobi and of the brothers Alexander and Wilhelm von Humboldt a new chair of geometry was founded for him at Berlin (1834). This he occupied until his death in Bern on 1 April 1863. He was described by Thomas Hirst as follows ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ernest De Jonquières
Ernest Jean Philippe Fauque de Jonquières (born Carpentras, France 3 July 1820; died Mousans-Sartoux, France 12 August 1901) was a French mathematician and naval officer who made several contributions in geometry. Jonquières attended the naval school at Brest, and later joined the French Navy. in 1841 he became a lieutenant, and from 1849 to 1850 he served on the staff of the Admiral in Paris. During this time, Jonquières became a close associate of Michel Chasles, whose works he had studied. During his subsequent time at sea, he continued his mathematical studies, and won a part of the Grand Prix of the French Academy of Sciences in 1862. In 1865, Jonquières became a captain and was sent to Saigon , population_density_km2 = 4,292 , population_density_metro_km2 = 697.2 , population_demonym = Saigonese , blank_name = GRP (Nominal) , blank_info = 2019 , blank1_name = – Total , blank1_ ... to organize a French agricul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
William Fulton (mathematician)
William Edgar Fulton (born August 29, 1939) is an American mathematician, specializing in algebraic geometry. Education and career He received his undergraduate degree from Brown University in 1961 and his doctorate from Princeton University in 1966. His Ph.D. thesis, written under the supervision of Gerard Washnitzer, was on ''The fundamental group of an algebraic curve''. Fulton worked at Princeton and Brandeis University from 1965 until 1970, when he began teaching at Brown. In 1987 he moved to the University of Chicago.Announcement of the 1996 s at the |
Robert MacPherson (mathematician)
Robert Duncan MacPherson (born May 25, 1944) is an American mathematician at the Institute for Advanced Study and Princeton University. He is best known for the invention of intersection homology with Mark Goresky, whose thesis he directed at Brown University, and who became his life partner. MacPherson previously taught at Brown University, the University of Paris, and the Massachusetts Institute of Technology. In 1983 he gave a plenary address at the International Congress of Mathematicians in Warsaw. Education and career Educated at Swarthmore College and Harvard University, MacPherson received his PhD from Harvard in 1970. His thesis, written under the direction of Raoul Bott, was entitled ''Singularities of Maps and Characteristic Classes''. Among his many PhD students are Kari Vilonen and Mark Goresky. Honors and awards In 1992, MacPherson was awarded the NAS Award in Mathematics from the National Academy of Sciences. In 2002 he and Goresky were awarded the Ler ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Projective Space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the '' complex'' lines through the origin of a complex Euclidean space (see below for an intuitive account). Formally, a complex projective space is the space of complex lines through the origin of an (''n''+1)-dimensional complex vector space. The space is denoted variously as P(C''n''+1), P''n''(C) or CP''n''. When , the complex projective space CP1 is the Riemann sphere, and when , CP2 is the complex projective plane (see there for a more elementary discussion). Complex projective space was first introduced by as an instance of what was then known as the "geometry of position", a notion originally due to Lazare Carnot, a kind of synthetic geometry that included other projective geometries as well. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bézout's Theorem
Bézout's theorem is a statement in algebraic geometry concerning the number of common zeros of polynomials in indeterminates. In its original form the theorem states that ''in general'' the number of common zeros equals the product of the degrees of the polynomials. It is named after Étienne Bézout. In some elementary texts, Bézout's theorem refers only to the case of two variables, and asserts that, if two plane algebraic curves of degrees d_1 and d_2 have no component in common, they have d_1d_2 intersection points, counted with their multiplicity, and including points at infinity and points with complex coordinates. In its modern formulation, the theorem states that, if is the number of common points over an algebraically closed field of projective hypersurfaces defined by homogeneous polynomials in indeterminates, then is either infinite, or equals the product of the degrees of the polynomials. Moreover, the finite case occurs almost always. In the case of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Veronese Surface
In mathematics, the Veronese surface is an algebraic surface in five-dimensional projective space, and is realized by the Veronese embedding, the embedding of the projective plane given by the complete linear system of conics. It is named after Giuseppe Veronese (1854–1917). Its generalization to higher dimension is known as the Veronese variety. The surface admits an embedding in the four-dimensional projective space defined by the projection from a general point in the five-dimensional space. Its general projection to three-dimensional projective space is called a Steiner surface. Definition The Veronese surface is the image of the mapping :\nu:\mathbb^2\to \mathbb^5 given by :\nu: :y:z\mapsto ^2:y^2:z^2:yz:xz:xy/math> where :\cdots/math> denotes homogeneous coordinates. The map \nu is known as the Veronese embedding. Motivation The Veronese surface arises naturally in the study of conics. A conic is a degree 2 plane curve, thus defined by an equation: :Ax^2 + Bxy + ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Blowing Up
In mathematics, blowing up or blowup is a type of geometric transformation which replaces a subspace of a given space with all the directions pointing out of that subspace. For example, the blowup of a point in a plane replaces the point with the projectivized tangent space at that point. The metaphor is that of zooming in on a photograph to enlarge part of the picture, rather than referring to an explosion. Blowups are the most fundamental transformation in birational geometry, because every birational morphism between projective varieties is a blowup. The weak factorization theorem says that every birational map can be factored as a composition of particularly simple blowups. The Cremona group, the group of birational automorphisms of the plane, is generated by blowups. Besides their importance in describing birational transformations, blowups are also an important way of constructing new spaces. For instance, most procedures for resolution of singularities proceed by b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |