|
Spiral Array Model
In music theory, the spiral array model is an extended type of pitch space. A mathematical model involving concentric helices (an "array of spirals"), it represents human perceptions of pitch (music), pitches, chord (music), chords, and key (music), keys in the same space, geometric space. It was proposed in 2000 by Elaine Chew in her MIT doctoral thesis ''Toward a Mathematical Model of Tonality''. Further research by Chew and others have produced modifications of the spiral array model, and, applied it to various problems in music theory and practice, such as key finding (symbolic and audio), pitch spelling, tonal segmentation, similarity assessment, and musical humor. The extensions and applications are described in ''Mathematical and Computational Modeling of Tonality: Theory and Applications''. The spiral array model can be viewed as a generalized tonnetz, which maps pitches into a two-dimensional lattice (array) structure. The spiral array wraps up the two-dimensional tonnetz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Music Theory
Music theory is the study of theoretical frameworks for understanding the practices and possibilities of music. ''The Oxford Companion to Music'' describes three interrelated uses of the term "music theory": The first is the "Elements of music, rudiments", that are needed to understand Musical notation, music notation (key signatures, time signatures, and Chord chart, rhythmic notation); the second is learning scholars' views on music from Ancient history, antiquity to the present; the third is a sub-topic of musicology that "seeks to define processes and general principles in music". The musicological approach to theory differs from music analysis "in that it takes as its starting-point not the individual work or performance but the fundamental materials from which it is built." Music theory is frequently concerned with describing how musicians and composers make music, including Musical tuning, tuning systems and composition methods among other topics. Because of the ever-expan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ITunes
iTunes is a media player, media library, and mobile device management (MDM) utility developed by Apple. It is used to purchase, play, download and organize digital multimedia on personal computers running the macOS and Windows operating systems, and can be used to rip songs from CDs as well as playing content from dynamic, smart playlists. It includes options for sound optimization and wirelessly sharing iTunes libraries. iTunes was announced by Apple CEO Steve Jobs on January 9, 2001. Its original and main focus was music, with a library offering organization and storage of Mac users' music collections. With the 2003 addition of the iTunes Store for purchasing and downloading digital music, and a Windows version of the program, it became an ubiquitous tool for managing music and configuring other features on Apple's line of iPod media players, which extended to the iPhone and iPad upon their introduction. From 2005 on, Apple expanded its core music features with s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Music Cognition
The psychology of music, or music psychology, is a branch of psychology, cognitive science, neuroscience, and/or musicology. It aims to explain and understand musical behaviour and experience, including the processes through which music is perceived, created, responded to, and incorporated into everyday life. Modern work in the psychology of music is primarily empirical; its knowledge tends to advance on the basis of interpretations of data collected by systematic observation of and interaction with human participants. In addition to its basic-science role in the cognitive sciences, the field has practical relevance for many areas, including music performance, composition, education, criticism, and therapy; investigations of human attitude, skill, performance, intelligence, creativity, and social behavior; and links between music and health. The psychology of music can shed light on non-psychological aspects of musicology and musical practice. For example, it contributes to musi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Music Theory
Music theory is the study of theoretical frameworks for understanding the practices and possibilities of music. ''The Oxford Companion to Music'' describes three interrelated uses of the term "music theory": The first is the "Elements of music, rudiments", that are needed to understand Musical notation, music notation (key signatures, time signatures, and Chord chart, rhythmic notation); the second is learning scholars' views on music from Ancient history, antiquity to the present; the third is a sub-topic of musicology that "seeks to define processes and general principles in music". The musicological approach to theory differs from music analysis "in that it takes as its starting-point not the individual work or performance but the fundamental materials from which it is built." Music theory is frequently concerned with describing how musicians and composers make music, including Musical tuning, tuning systems and composition methods among other topics. Because of the ever-expan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pitch Space
In music theory, pitch spaces model relationships between pitches. These models typically use distance to model the degree of relatedness, with closely related pitches placed near one another, and less closely related pitches farther apart. Depending on the complexity of the relationships under consideration, the models may be dimension, multidimensional. Models of pitch space are often Graph (discrete mathematics), graphs, group (mathematics), groups, lattice (music), lattices, or geometrical figures such as helixes. Pitch spaces distinguish octave-related pitches. When octave-related pitches are not distinguished, we have instead pitch class spaces, which represent relationships between pitch classes. (Some of these models are discussed in the entry on modulatory space, though readers should be advised that the term "modulatory space" is not a standard music-theoretical term.) Chordal spaces model relationships between chords. Linear and helical pitch space The simplest pitch ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spiral Array Model—Minor Key Representation
In mathematics, a spiral is a curve which emanates from a point, moving further away as it revolves around the point. It is a subtype of whorled patterns, a broad group that also includes concentric objects. Two-dimensional A two-dimensional, or plane, spiral may be easily described using polar coordinates, where the radius r is a monotonic continuous function of angle \varphi: * r=r(\varphi)\; . The circle would be regarded as a degenerate case (the function not being strictly monotonic, but rather constant). In ''x-y-coordinates'' the curve has the parametric representation: * x=r(\varphi)\cos\varphi \ ,\qquad y=r(\varphi)\sin\varphi\; . Examples Some of the most important sorts of two-dimensional spirals include: * The Archimedean spiral: r=a \varphi * The hyperbolic spiral: r = a/ \varphi * Fermat's spiral: r= a\varphi^ * The lituus: r = a\varphi^ * The logarithmic spiral: r=ae^ * The Cornu spiral or ''clothoid'' * The Fibonacci spiral and golden spiral * The S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Major Third
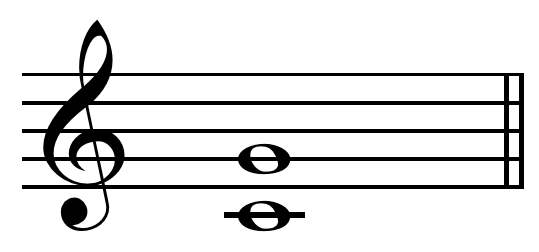
In music theory, a third is a Interval (music), musical interval encompassing three staff positions (see Interval (music)#Number, Interval number for more details), and the major third () is a third spanning four Semitone, half steps or two Whole step, whole steps. Along with the minor third, the major third is one of two commonly occurring thirds. It is described as ''major'' because it is the larger interval of the two: The major third spans four semitones, whereas the minor third only spans three. For example, the interval from C to E is a major third, as the note E lies four semitones above C, and there are three staff positions from C to E. Diminished third, Diminished and augmented thirds are shown on the musical staff the same number of lines and spaces apart, but contain a different number of semitones in pitch (two and five). Harmonic and non-harmonic thirds The major third may be derived from the harmonic series (music), harmonic series as the interval be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perfect Fifth
In music theory, a perfect fifth is the Interval (music), musical interval corresponding to a pair of pitch (music), pitches with a frequency ratio of 3:2, or very nearly so. In classical music from Western culture, a fifth is the interval from the first to the last of the first five consecutive Musical note, notes in a diatonic scale. The perfect fifth (often abbreviated P5) spans seven semitones, while the Tritone, diminished fifth spans six and the augmented fifth spans eight semitones. For example, the interval from C to G is a perfect fifth, as the note G lies seven semitones above C. The perfect fifth may be derived from the Harmonic series (music), harmonic series as the interval between the second and third harmonics. In a diatonic scale, the dominant (music), dominant note is a perfect fifth above the tonic (music), tonic note. The perfect fifth is more consonance and dissonance, consonant, or stable, than any other interval except the unison and the octave. It occu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
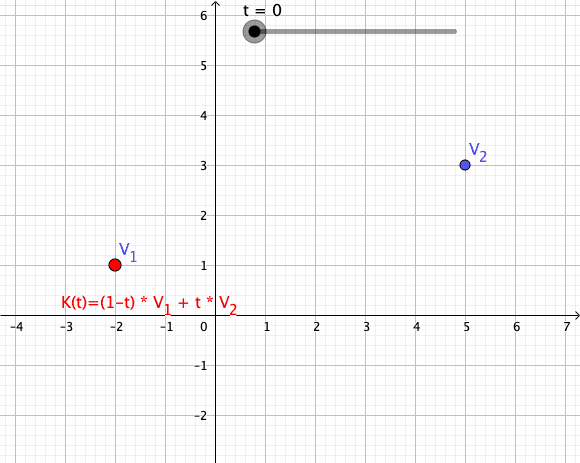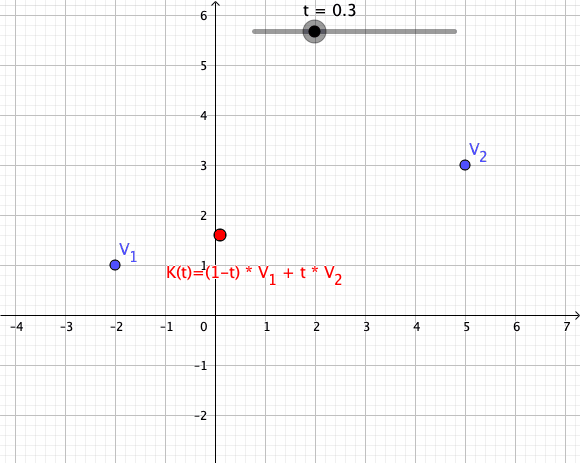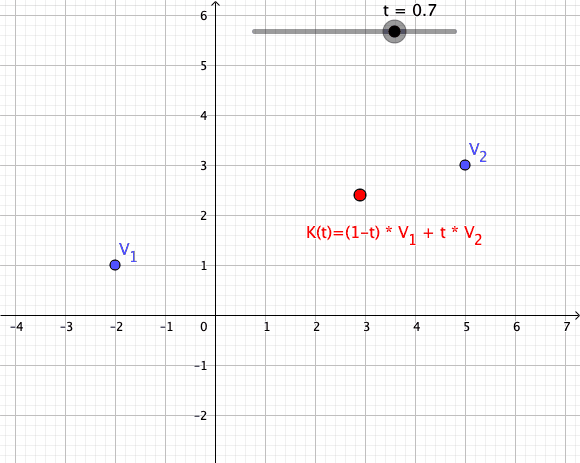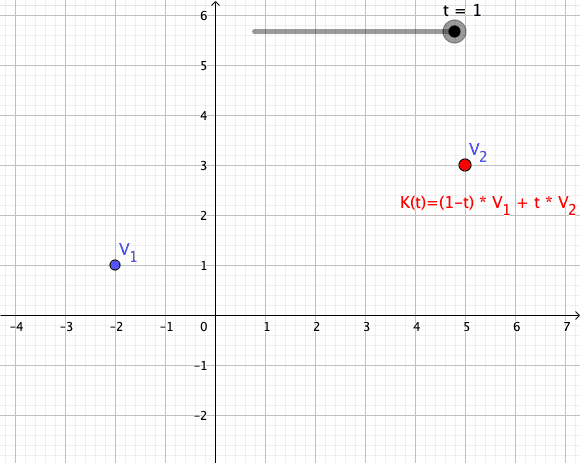
Convex Combination
In convex geometry and Vector space, vector algebra, a convex combination is a linear combination of point (geometry), points (which can be vector (geometric), vectors, scalar (mathematics), scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1. In other words, the operation is equivalent to a standard weighted average, but whose weights are expressed as a percent of the total weight, instead of as a fraction of the ''count'' of the weights as in a standard weighted average. Formal definition More formally, given a finite number of points x_1, x_2, \dots, x_n in a real vector space, a convex combination of these points is a point of the form : \alpha_1x_1+\alpha_2x_2+\cdots+\alpha_nx_n where the real numbers \alpha_i satisfy \alpha_i\ge 0 and \alpha_1+\alpha_2+\cdots+\alpha_n=1. As a particular example, every convex combination of two points lies on the line segment between the points. A set is convex set, convex if it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spiral Array Model—Nested Helices
In mathematics, a spiral is a curve which emanates from a point, moving further away as it revolves around the point. It is a subtype of whorled patterns, a broad group that also includes concentric objects. Two-dimensional A two-dimensional, or plane, spiral may be easily described using polar coordinates, where the radius r is a monotonic continuous function of angle \varphi: * r=r(\varphi)\; . The circle would be regarded as a degenerate case (the function not being strictly monotonic, but rather constant). In ''x-y-coordinates'' the curve has the parametric representation: * x=r(\varphi)\cos\varphi \ ,\qquad y=r(\varphi)\sin\varphi\; . Examples Some of the most important sorts of two-dimensional spirals include: * The Archimedean spiral: r=a \varphi * The hyperbolic spiral: r = a/ \varphi * Fermat's spiral: r= a\varphi^ * The lituus: r = a\varphi^ * The logarithmic spiral: r=ae^ * The Cornu spiral or ''clothoid'' * The Fibonacci spiral and golden spiral * The Sp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Enharmonic Equivalence
In music, two written notes have enharmonic equivalence if they produce the same pitch (music), pitch but are musical notation, notated differently. Similarly, written Interval (music), intervals, Chord (music), chords, or key signatures are considered enharmonic if they represent identical pitches that are notated differently. The term derives from Latin , in turn from Late Latin , from Ancient Greek (), from ('in') and ('harmony'). Definition The predominant musical tuning, tuning system in Western music is 12 tone equal temperament, twelve-tone equal temperament (12 ), where each octave is divided into twelve equivalent half steps or semitones. The notes F and G are a whole step apart, so the note one semitone above F (F) and the note one semitone below G (G) indicate the same pitch. These written notes are ''enharmonic'', or ''enharmonically equivalent''. The choice of notation for a pitch can depend on its diatonic function, role in harmony; this notation keeps modern ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |