|
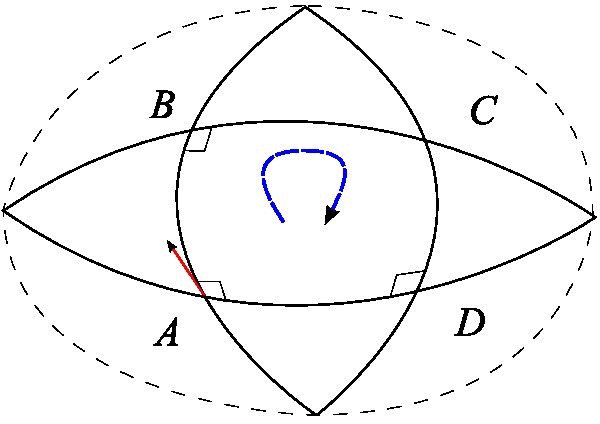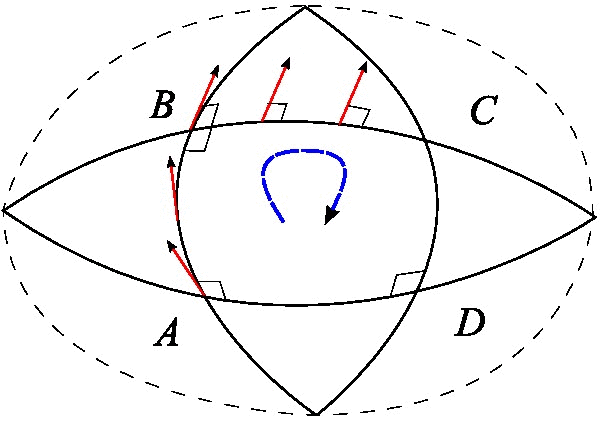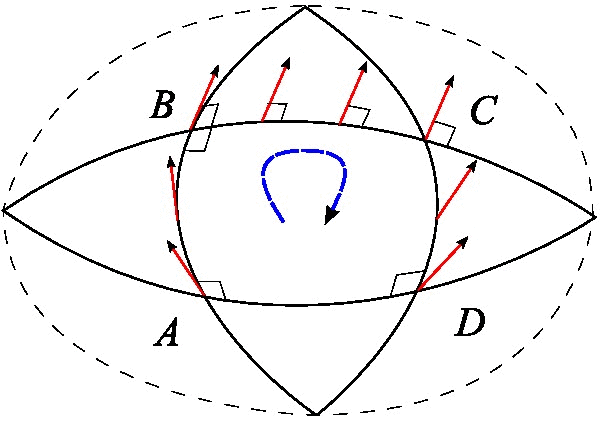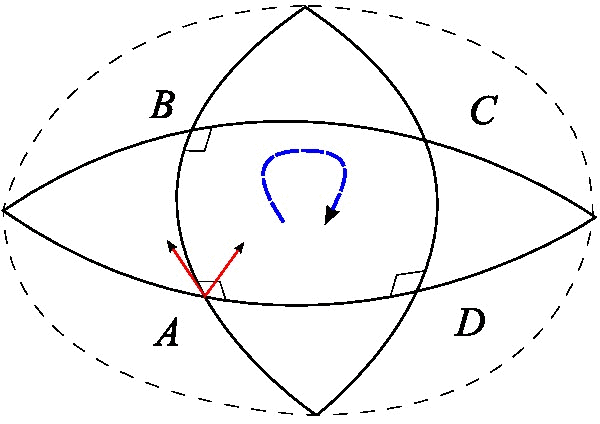
Space Curvature
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane. For curves, the canonical example is that of a circle, which has a curvature equal to the reciprocal of its radius. Smaller circles bend more sharply, and hence have higher curvature. The curvature ''at a point'' of a differentiable curve is the curvature of its osculating circle, that is the circle that best approximates the curve near this point. The curvature of a straight line is zero. In contrast to the tangent, which is a vector quantity, the curvature at a point is typically a scalar quantity, that is, it is expressed by a single real number. For surfaces (and, more generally for higher-dimensional manifolds), that are embedded in a Euclidean space, the concept of curvature is more complex, as it depends on the choice of a direction on the surface or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's Elements, Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension (mathematics), dimension, including the three-dimensional space and the ''Euclidean plane'' (dimension two). The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient History of geometry#Greek geometry, Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the Greek mathematics, ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of ''mathematical proof, proving'' all properties of the space as theorems, by starting from a few fundamental properties, called ''postulates'', which either were considered as eviden ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuously Differentiable
In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non-vertical tangent line at each interior point in its domain. A differentiable function is smooth (the function is locally well approximated as a linear function at each interior point) and does not contain any break, angle, or cusp. If is an interior point in the domain of a function , then is said to be ''differentiable at'' if the derivative f'(x_0) exists. In other words, the graph of has a non-vertical tangent line at the point . is said to be differentiable on if it is differentiable at every point of . is said to be ''continuously differentiable'' if its derivative is also a continuous function over the domain of the function f. Generally speaking, is said to be of class if its first k derivatives f^(x), f^(x), \ldots, f^(x) exist and are continuous over the domain of the func ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the "instantaneous rate of change", the ratio of the instantaneous change in the dependent variable to that of the independent variable. Derivatives can be generalized to functions of several real variables. In this generalization, the derivativ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Tangent Vector
Unit may refer to: Arts and entertainment * UNIT, a fictional military organization in the science fiction television series ''Doctor Who'' * Unit of action, a discrete piece of action (or beat) in a theatrical presentation Music * ''Unit'' (album), 1997 album by the Australian band Regurgitator * The Units, a synthpunk band Television * ''The Unit'', an American television series * '' The Unit: Idol Rebooting Project'', South Korean reality TV survival show Business * Stock keeping unit, a discrete inventory management construct * Strategic business unit, a profit center which focuses on product offering and market segment * Unit of account, a monetary unit of measurement * Unit coin, a small coin or medallion (usually military), bearing an organization's insignia or emblem * Work unit, the name given to a place of employment in the People's Republic of China Science and technology Science and medicine * Unit, a vessel or section of a chemical plant * Blood unit, a measurement ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arc Length
ARC may refer to: Business * Aircraft Radio Corporation, a major avionics manufacturer from the 1920s to the '50s * Airlines Reporting Corporation, an airline-owned company that provides ticket distribution, reporting, and settlement services * Airport Regions Conference, a European organization of major airports * Amalgamated Roadstone Corporation, a British stone quarrying company * American Record Company (1904–1908, re-activated 1979), one of two United States record labels by this name * American Record Corporation (1929–1938), a United States record label also known as American Record Company * ARC (American Recording Company) (1978-present), a vanity label for Earth, Wind & Fire * ARC Document Solutions, a company based in California, formerly American Reprographics Company * Amey Roadstone Construction, a former British construction company * Aqaba Railway Corporation, a freight railway in Jordan * ARC/Architectural Resources Cambridge, Inc., Cambridge, Massachusett ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Instantaneous Rate Of Change
In physics and the philosophy of science, instant refers to an infinitesimal interval in time, whose passage is instantaneous. In ordinary speech, an instant has been defined as "a point or very short space of time," a notion deriving from its etymological source, the Latin verb ''instare'', from ''in-'' + ''stare'' ('to stand'), meaning 'to stand upon or near.' The continuous nature of time and its infinite divisibility was addressed by Aristotle in his ''Physics'', where he wrote on Zeno's paradoxes. The philosopher and mathematician Bertrand Russell Bertrand Arthur William Russell, 3rd Earl Russell, (18 May 1872 – 2 February 1970) was a British mathematician, philosopher, logician, and public intellectual. He had a considerable influence on mathematics, logic, set theory, linguistics, ... was still seeking to define the exact nature of an instant thousands of years later. , the smallest time interval certify in regulated measurements is on the order of 397 zeptosecon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Foundations Of Science
''Foundations of Science'' is a peer-reviewed interdisciplinary academic journal focussing on methodological and philosophical topics concerning the structure and the growth of science. It is the official journal of the Association for Foundations of Science, Language and Cognition and is published quarterly by Springer Science+Business Media. The journal was established in 1995. The editor in chief is Diederik Aerts. Abstracting and indexing The journal is abstracted and indexed in Arts and Humanities Citation Index, Cengage, EBSCO Databases, FRANCIS, Google Scholar, Mathematical Reviews, PASCAL, Science Citation Index Expanded, Scopus, and Zentralblatt MATH. External links * Journal pageat the Free University of Brussels University of Brussels may refer to several institutions in Brussels, Belgium: Current institutions * Université libre de Bruxelles (ULB), a French-speaking university established as a separate entity in 1970 *Vrije Universiteit Brussel (VUB), a D ... ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal (geometry)
In geometry, a normal is an object such as a line, ray, or vector that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the (infinite) line perpendicular to the tangent line to the curve at the point. A normal vector may have length one (a unit vector) or its length may represent the curvature of the object (a ''curvature vector''); its algebraic sign may indicate sides (interior or exterior). In three dimensions, a surface normal, or simply normal, to a surface at point P is a vector perpendicular to the tangent plane of the surface at P. The word "normal" is also used as an adjective: a line ''normal'' to a plane, the ''normal'' component of a force, the normal vector, etc. The concept of normality generalizes to orthogonality (right angles). The concept has been generalized to differentiable manifolds of arbitrary dimension embedded in a Euclidean space. The normal vector space or normal space of a manifold at point P ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Augustin-Louis Cauchy
Baron Augustin-Louis Cauchy (, ; ; 21 August 178923 May 1857) was a French mathematician, engineer, and physicist who made pioneering contributions to several branches of mathematics, including mathematical analysis and continuum mechanics. He was one of the first to state and rigorously prove theorems of calculus, rejecting the heuristic principle of the generality of algebra of earlier authors. He almost singlehandedly founded complex analysis and the study of permutation groups in abstract algebra. A profound mathematician, Cauchy had a great influence over his contemporaries and successors; Hans Freudenthal stated: "More concepts and theorems have been named for Cauchy than for any other mathematician (in elasticity alone there are sixteen concepts and theorems named for Cauchy)." Cauchy was a prolific writer; he wrote approximately eight hundred research articles and five complete textbooks on a variety of topics in the fields of mathematics and mathematical physics. B ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nicole Oresme
Nicole Oresme (; c. 1320–1325 – 11 July 1382), also known as Nicolas Oresme, Nicholas Oresme, or Nicolas d'Oresme, was a French philosopher of the later Middle Ages. He wrote influential works on economics, mathematics, physics, astrology and astronomy, philosophy, and theology; was Bishop of Lisieux, a translator, a counselor of King Charles V of France, and one of the most original thinkers of 14th-century Europe. Life Nicole Oresme was born c. 1320–1325 in the village of Allemagnes (today's Fleury-sur-Orne) in the vicinity of Caen, Normandy, in the diocese of Bayeux. Practically nothing is known concerning his family. The fact that Oresme attended the royally sponsored and subsidised College of Navarre, an institution for students too poor to pay their expenses while studying at the University of Paris, makes it probable that he came from a peasant family. Oresme studied the "arts" in Paris, together with Jean Buridan (the so-called founder of the French school of natur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann Curvature Tensor
In the mathematical field of differential geometry, the Riemann curvature tensor or Riemann–Christoffel tensor (after Bernhard Riemann and Elwin Bruno Christoffel) is the most common way used to express the curvature of Riemannian manifolds. It assigns a tensor to each point of a Riemannian manifold (i.e., it is a tensor field). It is a local invariant of Riemannian metrics which measures the failure of the second covariant derivatives to commute. A Riemannian manifold has zero curvature if and only if it is ''flat'', i.e. locally isometric to the Euclidean space. The curvature tensor can also be defined for any pseudo-Riemannian manifold, or indeed any manifold equipped with an affine connection. It is a central mathematical tool in the theory of general relativity, the modern theory of gravity, and the curvature of spacetime is in principle observable via the geodesic deviation equation. The curvature tensor represents the tidal force experienced by a rigid body moving al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |