|
Solid Partition
Solid is a state of matter where molecules are closely packed and can not slide past each other. Solids resist compression, expansion, or external forces that would alter its shape, with the degree to which they are resisted dependent upon the specific material under consideration. Solids also always possess the least amount of kinetic energy per atom/molecule relative to other phases or, equivalently stated, solids are formed when matter in the liquid / gas phase is cooled below a certain temperature. This temperature is called the melting point of that substance and is an intrinsic property, i.e. independent of how much of the matter there is. All matter in solids can be arranged on a microscopic scale under certain conditions. Solids are characterized by structural rigidity and resistance to applied external forces and pressure. Unlike liquids, solids do not flow to take on the shape of their container, nor do they expand to fill the entire available volume like a gas. Much ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Diagram Of Water
This page provides supplementary data to the article properties of water. Further comprehensive authoritative data can be found at the ''NIST Chemistry WebBook'' page on thermophysical properties of fluids. Structure and properties Thermodynamic properties Liquid physical properties Water/steam equilibrium properties Vapor pressure formula for steam in equilibrium with liquid water: : \log_ P = A - \frac, where ''P'' is equilibrium vapor pressure in k Pa, and ''T'' is temperature in kelvins. For ''T'' = 273 K to 333 K: ''A'' = 7.2326; ''B'' = 1750.286; ''C'' = 38.1. For ''T'' = 333 K to 423 K: ''A'' = 7.0917; ''B'' = 1668.21; ''C'' = 45.1. Data in the table above is given for water–steam equilibria at various temperatures over the entire temperature range at which liquid water can exist. Pressure of the equilibrium is given in the second column in k Pa. The third column is the heat content of each gram of the liquid phase relative to water at 0 °C. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elastic Modulus
An elastic modulus (also known as modulus of elasticity (MOE)) is a quantity that describes an object's or substance's resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it. Definition The elastic modulus of an object is defined as the slope of its stress–strain curve in the elastic deformation region: A stiffer material will have a higher elastic modulus. An elastic modulus has the form: :\delta \ \stackrel\ \frac where stress is the force causing the deformation divided by the area to which the force is applied and strain is the ratio of the change in some parameter caused by the deformation to the original value of the parameter. Since strain is a dimensionless quantity, the units of \delta will be the same as the units of stress. Elastic constants and moduli Elastic constants are specific parameters that quantify the stiffness of a material in response to applied stresses and are fundamental in defining the elastic pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deformation (physics)
In physics and continuum mechanics, deformation is the change in the shape or size of an object. It has dimension of length with SI unit of metre (m). It is quantified as the residual displacement of particles in a non-rigid body, from an configuration to a configuration, excluding the body's average translation and rotation (its rigid transformation). A ''configuration'' is a set containing the positions of all particles of the body. A deformation can occur because of external loads, intrinsic activity (e.g. muscle contraction), body forces (such as gravity or electromagnetic forces), or changes in temperature, moisture content, or chemical reactions, etc. In a continuous body, a ''deformation field'' results from a stress field due to applied forces or because of some changes in the conditions of the body. The relation between stress and strain (relative deformation) is expressed by constitutive equations, e.g., Hooke's law for linear elastic materials. Deform ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
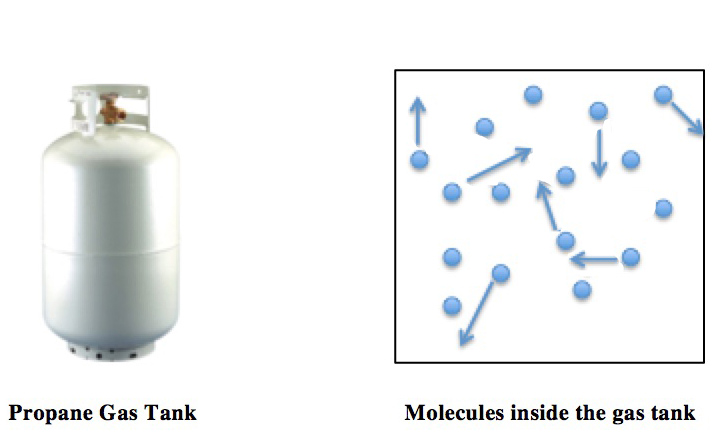
Ideal Gas Law
The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stated by Benoît Paul Émile Clapeyron in 1834 as a combination of the empirical Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. The ideal gas law is often written in an empirical form: pV = nRT where p, V and T are the pressure, volume and Thermodynamic temperature, temperature respectively; n is the amount of substance; and R is the ideal gas constant. It can also be derived from the microscopic kinetic theory of gases, kinetic theory, as was achieved (independently) by August Krönig in 1856 and Rudolf Clausius in 1857. Equation The state function, state of an amount of gas is determined by its pressure, volume, and temperature. The modern form of the equation relates these simply in two main forms. The temperature us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electron Degeneracy Pressure
In astrophysics and condensed matter physics, electron degeneracy pressure is a quantum mechanical effect critical to understanding the stability of white dwarf stars and metal solids. It is a manifestation of the more general phenomenon of quantum degeneracy pressure. The term "degenerate" here is not related to degenerate energy levels, but to Fermi–Dirac statistics close to the zero-temperature limit (temperatures much smaller than the Fermi temperature, which for metals is about 10,000 K.) In metals and in white dwarf stars, electrons can be modeled as a gas of non-interacting electrons confined to a finite volume. Although there are strong electromagnetic forces between the negatively charged electrons, these forces are approximately balanced by the positive nuclei and so can be neglected in the simplest models. The pressure exerted by the electrons is related to their kinetic energy. The degeneracy pressure is most prominent at low temperatures: If electrons wer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volume
Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch). The definition of length and height (cubed) is interrelated with volume. The volume of a container is generally understood to be the capacity of the container; i.e., the amount of fluid (gas or liquid) that the container could hold, rather than the amount of space the container itself displaces. By metonymy, the term "volume" sometimes is used to refer to the corresponding region (e.g., bounding volume). In ancient times, volume was measured using similar-shaped natural containers. Later on, standardized containers were used. Some simple three-dimensional shapes can have their volume easily calculated using arithmetic formulas. Volumes of more complicated shapes can be calculated with integral calculus if a formula exists for the shape ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compression (physics)
In mechanics, compression is the application of balanced inward ("pushing") forces to different points on a material or Structural system, structure, that is, forces with no Net force, net sum or torque directed so as to reduce its size in one or more directions.Ferdinand Pierre Beer, Elwood Russell Johnston, John T. DeWolf (1992), "Mechanics of Materials". (Book) McGraw-Hill Professional, It is contrasted with tension (physics), tension or traction, the application of balanced outward ("pulling") forces; and with shear stress, shearing forces, directed so as to displace layers of the material parallel to each other. The compressive strength of materials and structures is an important engineering consideration. In uniaxial compression, the forces are directed along one direction only, so that they act towards decreasing the object's length along that direction. The compressive forces may also be applied in multiple directions; for example inwards along the edges of a plate or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Porosity
Porosity or void fraction is a measure of the void (i.e. "empty") spaces in a material, and is a fraction of the volume of voids over the total volume, between 0 and 1, or as a percentage between 0% and 100%. Strictly speaking, some tests measure the "accessible void", the total amount of void space accessible from the surface (cf. closed-cell foam). There are many ways to test porosity in a substance or part, such as industrial CT scanning. The term porosity is used in multiple fields including pharmaceutics, ceramics, metallurgy, materials, manufacturing, petrophysics, hydrology, earth sciences, soil mechanics, rock mechanics, and engineering. Void fraction in two-phase flow In gas-liquid two-phase flow, the void fraction is defined as the fraction of the flow-channel volume that is occupied by the gas phase or, alternatively, as the fraction of the cross-sectional area of the channel that is occupied by the gas phase. Void fraction usually varies from location to l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Calcium Carbonate
Calcium carbonate is a chemical compound with the chemical formula . It is a common substance found in Rock (geology), rocks as the minerals calcite and aragonite, most notably in chalk and limestone, eggshells, gastropod shells, shellfish skeletons and pearls. Materials containing much calcium carbonate or resembling it are described as calcareous. Calcium carbonate is the active ingredient in agricultural lime and is produced when calcium ions in hard water react with carbonate ions to form limescale. It has medical use as a calcium supplement or as an antacid, but excessive consumption can be hazardous and cause hypercalcemia and digestive issues. Chemistry Calcium carbonate shares the typical properties of other carbonates. Notably, it: *reacts with acids, releasing carbonic acid which quickly disintegrates into carbon dioxide and water: : *releases carbon dioxide upon heating, called a thermal decomposition reaction, or calcination (to above 840 °C in the case of ), t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
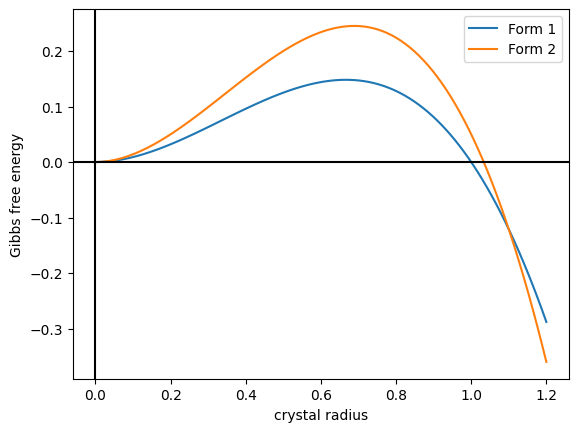
Crystal Polymorphism
In crystallography, polymorphism is the phenomenon where a compound or element can crystallize into more than one crystal structure. The preceding definition has evolved over many years and is still under discussion today. Discussion of the defining characteristics of polymorphism involves distinguishing among types of transitions and structural changes occurring in polymorphism versus those in other phenomena. Overview Phase transitions (phase changes) that help describe polymorphism include polymorphic transitions as well as melting and vaporization transitions. According to IUPAC, a polymorphic transition is "A reversible transition of a solid crystalline phase at a certain temperature and pressure (the inversion point) to another phase of the same chemical composition with a different crystal structure." Additionally, Walter McCrone described the phases in polymorphic matter as "different in crystal structure but identical in the liquid or vapor states." McCrone also defin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carbon
Carbon () is a chemical element; it has chemical symbol, symbol C and atomic number 6. It is nonmetallic and tetravalence, tetravalent—meaning that its atoms are able to form up to four covalent bonds due to its valence shell exhibiting 4 electrons. It belongs to group 14 of the periodic table. Carbon makes up about 0.025 percent of Earth's crust. Three Isotopes of carbon, isotopes occur naturally, carbon-12, C and carbon-13, C being stable, while carbon-14, C is a radionuclide, decaying with a half-life of 5,700 years. Carbon is one of the timeline of chemical element discoveries#Pre-modern and early modern discoveries, few elements known since antiquity. Carbon is the 15th abundance of elements in Earth's crust, most abundant element in the Earth's crust, and the abundance of the chemical elements, fourth most abundant element in the universe by mass after hydrogen, helium, and oxygen. Carbon's abundance, its unique diversity of organic compounds, and its unusual abi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |