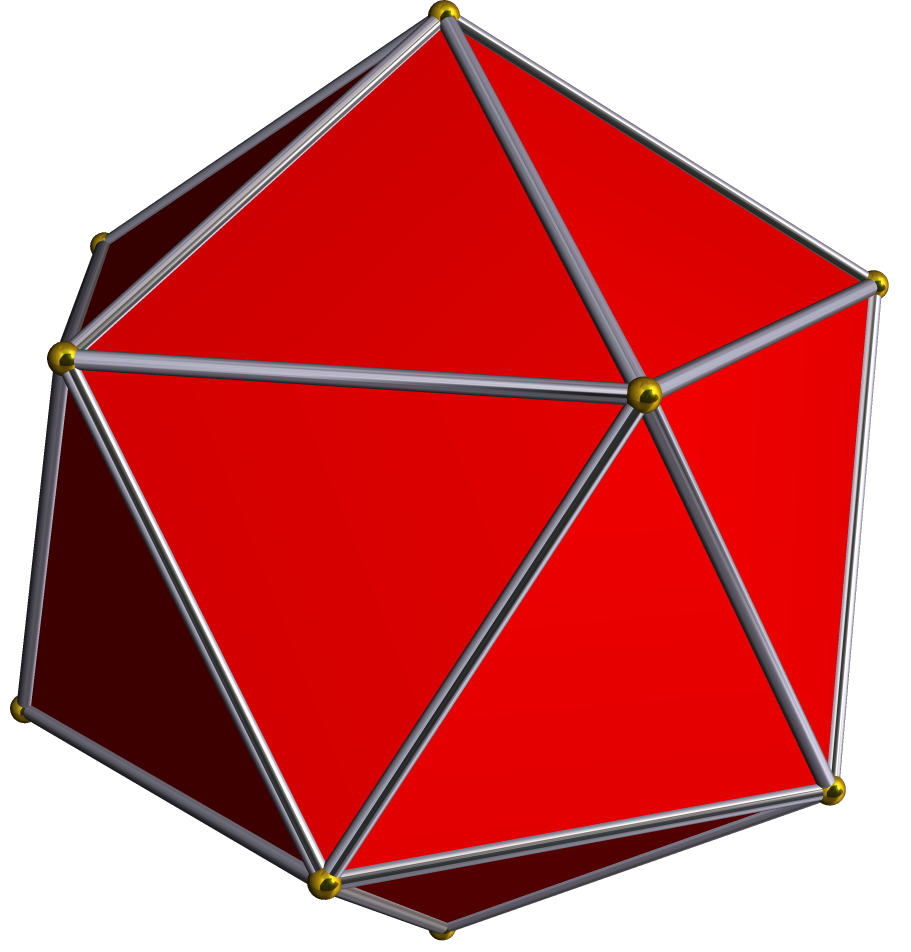
|
Small Complex Icosidodecahedron
In geometry, the small complex icosidodecahedron is a degenerate uniform star polyhedron. Its edges are doubled, making it degenerate. The star has 32 faces (20 triangles and 12 pentagons), 60 (doubled) edges and 12 vertices and 4 sharing faces. The faces in it are considered as two overlapping edges as topological polyhedron. A small complex icosidodecahedron can be constructed from a number of different vertex figures. A very similar figure emerges as a geometrical truncation of the great stellated dodecahedron, where the pentagram faces become doubly-wound pentagons ( --> ), making the internal pentagonal planes, and the three meeting at each vertex become triangles, making the external triangular planes. As a compound The small complex icosidodecahedron can be seen as a compound of the icosahedron and the great dodecahedron where all vertices are precise and edges coincide. The small complex icosidodecahedron resembles an icosahedron, because the great dodecahedron is c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Polytope
In geometry, a pentagonal polytope is a regular polytope in ''n'' dimensions constructed from the H''n'' Coxeter group. The family was named by H. S. M. Coxeter, because the two-dimensional pentagonal polytope is a pentagon. It can be named by its Schläfli symbol as (dodecahedral) or (icosahedral). Family members The family starts as 1-polytopes and ends with ''n'' = 5 as infinite tessellations of 4-dimensional hyperbolic space. There are two types of pentagonal polytopes; they may be termed the ''dodecahedral'' and ''icosahedral'' types, by their three-dimensional members. The two types are duals of each other. Dodecahedral The complete family of dodecahedral pentagonal polytopes are: # Line segment, # Pentagon, # Dodecahedron, (12 pentagonal faces) # 120-cell, (120 dodecahedral cells) # Order-3 120-cell honeycomb, (tessellates hyperbolic 4-space (∞ 120-cell facets) The facets of each dodecahedral pentagonal polytope are the dodecahedral pentagonal polytopes o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Complex Rhombicosidodecahedron
In geometry, the small complex rhombicosidodecahedron (also known as the small complex ditrigonal rhombicosidodecahedron) is a degenerate uniform star polyhedron. It has 62 faces (20 triangles, 12 pentagrams and 30 squares), 120 (doubled) edges and 20 vertices. All edges are doubled (making it degenerate), sharing 4 faces, but are considered as two overlapping edges as a topological polyhedron. It can be constructed from the vertex figure 3(5/2.4.3.4), thus making it also a cantellated great icosahedron. The "3" in front of this vertex figure indicates that each vertex in this degenerate polyhedron is in fact three coincident vertices. It may also be given the Schläfli symbol rr or t0,2. As a compound It can be seen as a compound of the small ditrigonal icosidodecahedron, U30, and the compound of five cubes. It is also a faceting of the dodecahedron. As a cantellation It can also be seen as a cantellation of the great icosahedron (or, equivalently, of the great stella ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Rhombidodecadodecahedron
Complex commonly refers to: * Complexity, the behaviour of a system whose components interact in multiple ways so possible interactions are difficult to describe ** Complex system, a system composed of many components which may interact with each other * Complex (psychology), a core pattern of emotions etc. in the personal unconscious organized around a common theme such as power or status Complex may also refer to: Arts, entertainment and media * Complex (English band), formed in 1968, and their 1971 album ''Complex'' * Complex (band), a Japanese rock band * ''Complex'' (album), by Montaigne, 2019, and its title track * ''Complex'' (EP), by Rifle Sport, 1985 * "Complex" (song), by Gary Numan, 1979 * Complex Networks, publisher of magazine ''Complex'', now online Biology * Protein–ligand complex, a complex of a protein bound with a ligand * Exosome complex, a multi-protein intracellular complex * Protein complex, a group of two or more associated polypeptide chains * Sp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small Complex Rhombicosidodecahedron
In geometry, the small complex rhombicosidodecahedron (also known as the small complex ditrigonal rhombicosidodecahedron) is a degenerate uniform star polyhedron. It has 62 faces (20 triangles, 12 pentagrams and 30 squares), 120 (doubled) edges and 20 vertices. All edges are doubled (making it degenerate), sharing 4 faces, but are considered as two overlapping edges as a topological polyhedron. It can be constructed from the vertex figure 3(5/2.4.3.4), thus making it also a cantellated great icosahedron. The "3" in front of this vertex figure indicates that each vertex in this degenerate polyhedron is in fact three coincident vertices. It may also be given the Schläfli symbol rr or t0,2. As a compound It can be seen as a compound of the small ditrigonal icosidodecahedron, U30, and the compound of five cubes. It is also a faceting of the dodecahedron. As a cantellation It can also be seen as a cantellation of the great icosahedron (or, equivalently, of the great stella ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Complex Icosidodecahedron
In geometry, the great complex icosidodecahedron is a degenerate uniform star polyhedron. It has 12 vertices, and 60 (doubled) edges, and 32 faces, 12 pentagrams and 20 triangles. All edges are doubled (making it degenerate), sharing 4 faces, but are considered as two overlapping edges as topological polyhedron. It can be constructed from a number of different vertex figures. As a compound The great complex icosidodecahedron can be considered a compound of the small stellated dodecahedron, , and great icosahedron, , sharing the same vertices and edges, while the second is hidden, being completely contained inside the first. {, , {, class=wikitable width=300 , + Compound polyhedron , , , , - align=center , Small stellated dodecahedron , Great icosahedron , Compound See also *Small complex icosidodecahedron *Small complex rhombicosidodecahedron *Complex rhombidodecadodecahedron *Great complex rhombicosidodecahedron In geometry, the small complex rhombicosidodecahe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagram
A pentagram (sometimes known as a pentalpha, pentangle, or star pentagon) is a regular five-pointed star polygon, formed from the diagonal line segments of a convex (or simple, or non-self-intersecting) regular pentagon. Drawing a circle around the five points creates a similar symbol referred to as the pentacle, which is used widely by Wiccans and in paganism, or as a sign of life and connections. The word "pentagram" refers only to the five-pointed star, not the surrounding circle of a pentacle. Pentagrams were used symbolically in ancient Greece and Babylonia. Christians once commonly used the pentagram to represent the Five Holy Wounds, five wounds of Jesus. Today the symbol is widely used by the Wiccans, witches, and pagans. The pentagram has Magic (supernatural), magical associations. Many people who practice neopaganism wear jewelry incorporating the symbol. The word ''pentagram'' comes from the Greek language, Greek word πεντάγραμμον (''pentagrammon''), fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complete Graph K5
Complete may refer to: Logic * Completeness (logic) * Completeness of a theory, the property of a theory that every formula in the theory's language or its negation is provable Mathematics * The completeness of the real numbers, which implies that there are no "holes" in the real numbers * Complete metric space, a metric space in which every Cauchy sequence converges * Complete uniform space, a uniform space where every Cauchy net in converges (or equivalently every Cauchy filter converges) * Complete measure, a measure space where every subset of every null set is measurable * Completion (algebra), at an ideal * Completeness (cryptography) * Completeness (statistics), a statistic that does not allow an unbiased estimator of zero * Complete graph, an undirected graph in which every pair of vertices has exactly one edge connecting them * Complete category, a category ''C'' where every diagram from a small category to ''C'' has a limit; it is ''cocomplete'' if every such functor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Star Polygon 5-2
A star is an astronomical object comprising a luminous spheroid of plasma held together by its gravity. The nearest star to Earth is the Sun. Many other stars are visible to the naked eye at night, but their immense distances from Earth make them appear as fixed points of light. The most prominent stars have been categorised into constellations and asterisms, and many of the brightest stars have proper names. Astronomers have assembled star catalogues that identify the known stars and provide standardized stellar designations. The observable universe contains an estimated to stars. Only about 4,000 of these stars are visible to the naked eye, all within the Milky Way galaxy. A star's life begins with the gravitational collapse of a gaseous nebula of material composed primarily of hydrogen, along with helium and trace amounts of heavier elements. Its total mass is the main factor determining its evolution and eventual fate. A star shines for most of its active life due to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagon
In geometry, a pentagon (from the Greek πέντε ''pente'' meaning ''five'' and γωνία ''gonia'' meaning ''angle'') is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°. A pentagon may be simple or self-intersecting. A self-intersecting ''regular pentagon'' (or ''star pentagon'') is called a pentagram. Regular pentagons A '' regular pentagon'' has Schläfli symbol and interior angles of 108°. A '' regular pentagon'' has five lines of reflectional symmetry, and rotational symmetry of order 5 (through 72°, 144°, 216° and 288°). The diagonals of a convex regular pentagon are in the golden ratio to its sides. Given its side length t, its height H (distance from one side to the opposite vertex), width W (distance between two farthest separated points, which equals the diagonal length D) and circumradius R are given by: :\begin H &= \frac~t \approx 1.539~t, \\ W= D &= \frac~t\approx 1.618~t, \\ W &= \sqr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagram
A pentagram (sometimes known as a pentalpha, pentangle, or star pentagon) is a regular five-pointed star polygon, formed from the diagonal line segments of a convex (or simple, or non-self-intersecting) regular pentagon. Drawing a circle around the five points creates a similar symbol referred to as the pentacle, which is used widely by Wiccans and in paganism, or as a sign of life and connections. The word "pentagram" refers only to the five-pointed star, not the surrounding circle of a pentacle. Pentagrams were used symbolically in ancient Greece and Babylonia. Christians once commonly used the pentagram to represent the Five Holy Wounds, five wounds of Jesus. Today the symbol is widely used by the Wiccans, witches, and pagans. The pentagram has Magic (supernatural), magical associations. Many people who practice neopaganism wear jewelry incorporating the symbol. The word ''pentagram'' comes from the Greek language, Greek word πεντάγραμμον (''pentagrammon''), fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
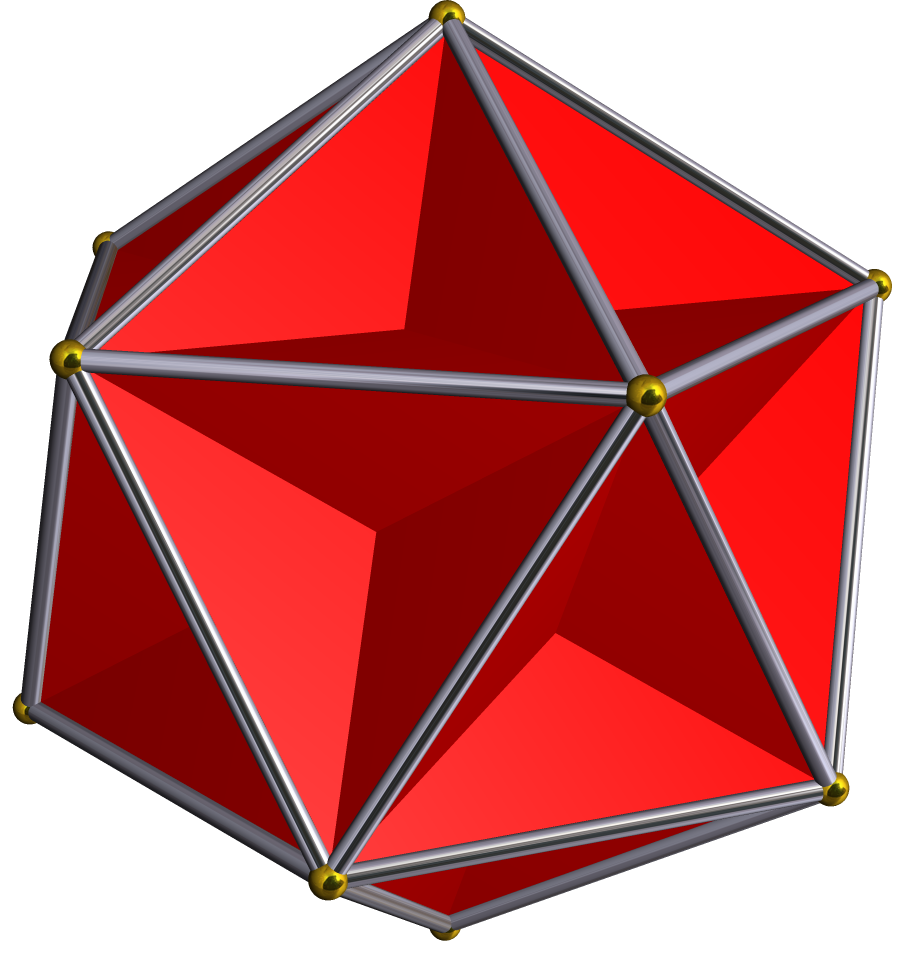
Small Complex Icosidodecahedron
In geometry, the small complex icosidodecahedron is a degenerate uniform star polyhedron. Its edges are doubled, making it degenerate. The star has 32 faces (20 triangles and 12 pentagons), 60 (doubled) edges and 12 vertices and 4 sharing faces. The faces in it are considered as two overlapping edges as topological polyhedron. A small complex icosidodecahedron can be constructed from a number of different vertex figures. A very similar figure emerges as a geometrical truncation of the great stellated dodecahedron, where the pentagram faces become doubly-wound pentagons ( --> ), making the internal pentagonal planes, and the three meeting at each vertex become triangles, making the external triangular planes. As a compound The small complex icosidodecahedron can be seen as a compound of the icosahedron and the great dodecahedron where all vertices are precise and edges coincide. The small complex icosidodecahedron resembles an icosahedron, because the great dodecahedron is c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
