|
Shannon–Hartley Theorem
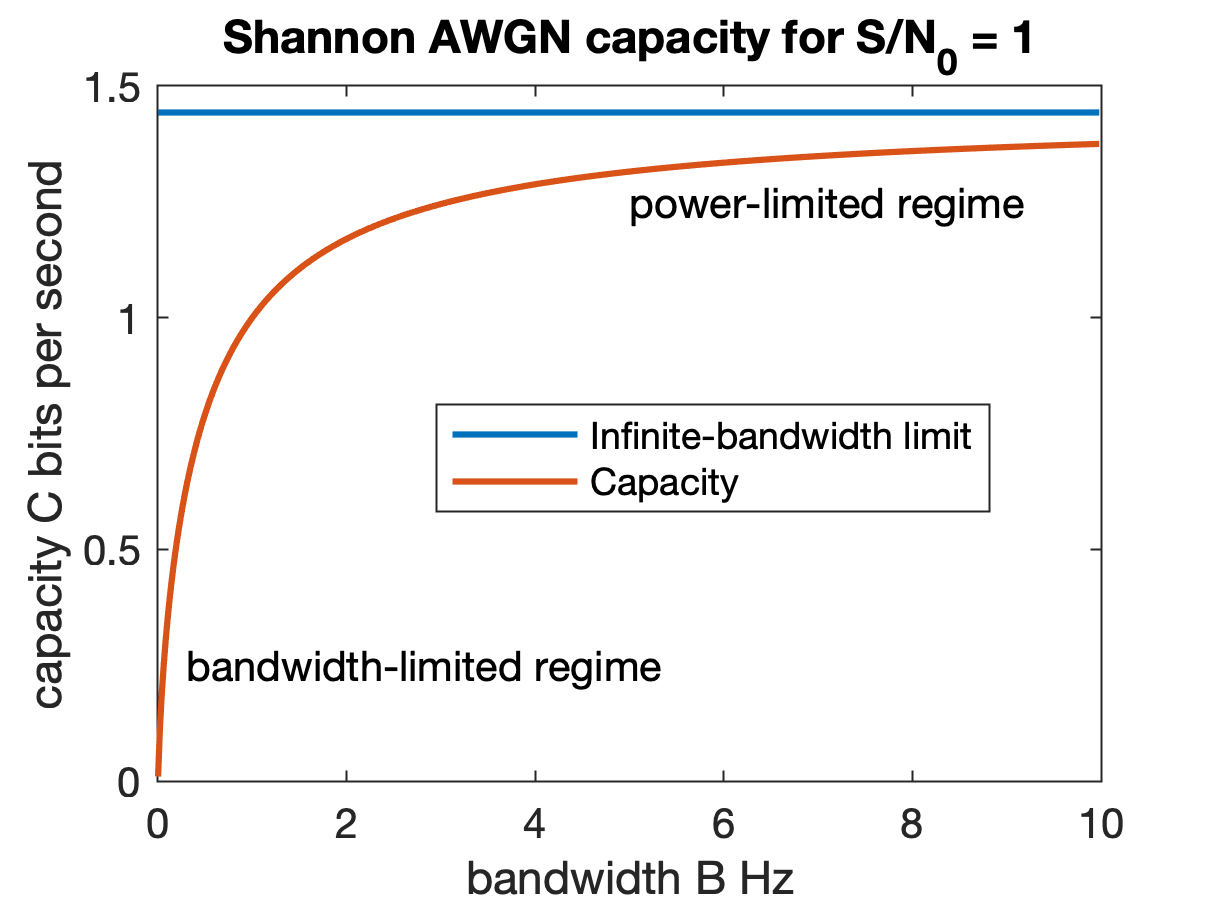
In information theory, the Shannon–Hartley theorem tells the maximum rate at which information can be transmitted over a communications channel of a specified bandwidth in the presence of noise. It is an application of the noisy-channel coding theorem to the archetypal case of a continuous-time analog communications channel subject to Gaussian noise. The theorem establishes Shannon's channel capacity for such a communication link, a bound on the maximum amount of error-free information per time unit that can be transmitted with a specified bandwidth in the presence of the noise interference, assuming that the signal power is bounded, and that the Gaussian noise process is characterized by a known power or power spectral density. The law is named after Claude Shannon and Ralph Hartley. Statement of the theorem The Shannon–Hartley theorem states the channel capacity C, meaning the theoretical tightest upper bound on the information rate of data that can be communicated at a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Theory
Information theory is the scientific study of the quantification (science), quantification, computer data storage, storage, and telecommunication, communication of information. The field was originally established by the works of Harry Nyquist and Ralph Hartley, in the 1920s, and Claude Shannon in the 1940s. The field is at the intersection of probability theory, statistics, computer science, statistical mechanics, information engineering (field), information engineering, and electrical engineering. A key measure in information theory is information entropy, entropy. Entropy quantifies the amount of uncertainty involved in the value of a random variable or the outcome of a random process. For example, identifying the outcome of a fair coin flip (with two equally likely outcomes) provides less information (lower entropy) than specifying the outcome from a roll of a dice, die (with six equally likely outcomes). Some other important measures in information theory are mutual informat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bits Per Second
In telecommunications and computing, bit rate (bitrate or as a variable ''R'') is the number of bits that are conveyed or processed per unit of time. The bit rate is expressed in the unit bit per second (symbol: bit/s), often in conjunction with an SI prefix such as kilo (1 kbit/s = 1,000 bit/s), mega (1 Mbit/s = 1,000 kbit/s), giga (1 Gbit/s = 1,000 Mbit/s) or tera (1 Tbit/s = 1,000 Gbit/s). The non-standard abbreviation bps is often used to replace the standard symbol bit/s, so that, for example, 1 Mbps is used to mean one million bits per second. In most computing and digital communication environments, one byte per second (symbol: B/s) corresponds to 8 bit/s. Prefixes When quantifying large or small bit rates, SI prefixes (also known as metric prefixes or decimal prefixes) are used, thus: Binary prefixes are sometimes used for bit rates. The International Standard ( IEC 80000-13) specifies different ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithm
In mathematics, the logarithm is the inverse function to exponentiation. That means the logarithm of a number to the base is the exponent to which must be raised, to produce . For example, since , the ''logarithm base'' 10 of is , or . The logarithm of to ''base'' is denoted as , or without parentheses, , or even without the explicit base, , when no confusion is possible, or when the base does not matter such as in big O notation. The logarithm base is called the decimal or common logarithm and is commonly used in science and engineering. The natural logarithm has the number as its base; its use is widespread in mathematics and physics, because of its very simple derivative. The binary logarithm uses base and is frequently used in computer science. Logarithms were introduced by John Napier in 1614 as a means of simplifying calculations. They were rapidly adopted by navigators, scientists, engineers, surveyors and others to perform high-a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Data Signalling Rate
In telecommunication, data signaling rate (DSR), also known as gross bit rate, is the aggregate rate at which data passes a point in the transmission path of a data transmission system. # The DSR is usually expressed in bits per second. # The data signaling rate is given by \sum_^ \frac where ''m'' is the number of parallel channels, ''ni'' is the number of significant conditions of the modulation in the ''i''-th channel, and ''Ti'' is the unit interval, expressed in seconds, for the ''i''-th channel. # For serial transmission in a single channel, the DSR reduces to (1/''T'')log2''n''; with a two-condition modulation, i. e. ''n'' = 2, the DSR is 1/''T'', according to Hartley's law. # For parallel transmission with equal unit intervals and equal numbers of significant conditions on each channel, the DSR is (''m''/''T'')log2''n''; in the case of a two-condition modulation, this reduces to ''m''/''T''. # The DSR may be expressed in bauds, in which case, the factor log2''ni'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line Rate
In telecommunications and computing, bit rate (bitrate or as a variable ''R'') is the number of bits that are conveyed or processed per unit of time. The bit rate is expressed in the unit bit per second (symbol: bit/s), often in conjunction with an SI prefix such as kilo (1 kbit/s = 1,000 bit/s), mega (1 Mbit/s = 1,000 kbit/s), giga (1 Gbit/s = 1,000 Mbit/s) or tera (1 Tbit/s = 1,000 Gbit/s). The non-standard abbreviation bps is often used to replace the standard symbol bit/s, so that, for example, 1 Mbps is used to mean one million bits per second. In most computing and digital communication environments, one byte per second (symbol: B/s) corresponds to 8 bit/s. Prefixes When quantifying large or small bit rates, SI prefixes (also known as metric prefixes or decimal prefixes) are used, thus: Binary prefixes are sometimes used for bit rates. The International Standard ( IEC 80000-13) specifies different a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nyquist Rate
In signal processing, the Nyquist rate, named after Harry Nyquist, is a value (in units of samples per second or hertz, Hz) equal to twice the highest frequency (bandwidth) of a given function or signal. When the function is digitized at a higher sample rate (see ), the resulting discrete-time sequence is said to be free of the distortion known as aliasing. Conversely, for a given sample-rate the corresponding Nyquist frequency in Hz is one-half the sample-rate. Note that the ''Nyquist rate'' is a property of a continuous-time signal, whereas ''Nyquist frequency'' is a property of a discrete-time system. The term ''Nyquist rate'' is also used in a different context with units of symbols per second, which is actually the field in which Harry Nyquist was working. In that context it is an upper bound for the symbol rate across a bandwidth-limited baseband channel such as a telegraph line or passband channel such as a limited radio frequency band or a frequency division mult ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Telegraph
Telegraphy is the long-distance transmission of messages where the sender uses symbolic codes, known to the recipient, rather than a physical exchange of an object bearing the message. Thus flag semaphore is a method of telegraphy, whereas pigeon post is not. Ancient signalling systems, although sometimes quite extensive and sophisticated as in China, were generally not capable of transmitting arbitrary text messages. Possible messages were fixed and predetermined and such systems are thus not true telegraphs. The earliest true telegraph put into widespread use was the optical telegraph of Claude Chappe, invented in the late 18th century. The system was used extensively in France, and European nations occupied by France, during the Napoleonic era. The electric telegraph started to replace the optical telegraph in the mid-19th century. It was first taken up in Britain in the form of the Cooke and Wheatstone telegraph, initially used mostly as an aid to railway signalling. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harry Nyquist
Harry Nyquist (, ; February 7, 1889 – April 4, 1976) was a Swedish-American physicist and electronic engineer who made important contributions to communication theory. Personal life Nyquist was born in the village Nilsby of the parish Stora Kil, Värmland, Sweden. He was the son of Lars Jonsson Nyqvist (b. 1847) and Katrina Eriksdotter (b. 1857). His parents had eight children: Elin Teresia, Astrid, Selma, Harry Theodor, Amelie, Olga Maria, Axel Martin and Herta Alfrida. He emigrated to the USA in 1907. Education He entered the University of North Dakota in 1912 and received B.S. and M.S. degrees in electrical engineering in 1914 and 1915, respectively. He received a Ph.D. in physics at Yale University in 1917. Career He worked at AT&T's Department of Development and Research from 1917 to 1934, and continued when it became Bell Telephone Laboratories that year, until his retirement in 1954. Nyquist received the IRE Medal of Honor in 1960 for "fundamental contributions to a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decibels
The decibel (symbol: dB) is a relative unit of measurement equal to one tenth of a bel (B). It expresses the ratio of two values of a Power, root-power, and field quantities, power or root-power quantity on a logarithmic scale. Two signals whose level (logarithmic quantity), levels differ by one decibel have a power ratio of 101/10 (approximately ) or root-power ratio of 10 (approximately ). The unit expresses a relative change or an absolute value. In the latter case, the numeric value expresses the ratio of a value to a fixed reference value; when used in this way, the unit symbol is often suffixed with letter codes that indicate the reference value. For example, for the reference value of 1 volt, a common suffix is "#Voltage, V" (e.g., "20 dBV"). Two principal types of scaling of the decibel are in common use. When expressing a power ratio, it is defined as ten times the Common logarithm, logarithm in base 10. That is, a change in ''power'' by a factor of 10 corresp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carrier-to-noise Ratio
In telecommunications, the carrier-to-noise ratio, often written CNR or ''C/N'', is the signal-to-noise ratio (SNR) of a modulated signal. The term is used to distinguish the CNR of the radio frequency passband signal from the SNR of an analog base band message signal after demodulation. For example, with FM radio, the strength of the 100 MHz carrier with modulations would be considered for CNR, whereas the audio frequency analogue message signal would be for SNR; in each case, compared to the apparent noise. If this distinction is not necessary, the term SNR is often used instead of CNR, with the same definition. Digitally modulated signals (e.g. QAM or PSK) are basically made of two CW carriers (the I and Q components, which are out-of-phase carriers). In fact, the information (bits or symbols) is carried by given combinations of phase and/or amplitude of the I and Q components. It is for this reason that, in the context of digital modulations, digitally modulated signals ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal-to-noise Ratio
Signal-to-noise ratio (SNR or S/N) is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. SNR is defined as the ratio of signal power to the noise power, often expressed in decibels. A ratio higher than 1:1 (greater than 0 dB) indicates more signal than noise. SNR, bandwidth, and channel capacity of a communication channel are connected by the Shannon–Hartley theorem. Definition Signal-to-noise ratio is defined as the ratio of the power of a signal (meaningful input) to the power of background noise (meaningless or unwanted input): : \mathrm = \frac, where is average power. Both signal and noise power must be measured at the same or equivalent points in a system, and within the same system bandwidth. Depending on whether the signal is a constant () or a random variable (), the signal-to-noise ratio for random noise becomes: : \mathrm = \frac where E refers to the expected value, i.e. in this case ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carrier-to-noise Ratio
In telecommunications, the carrier-to-noise ratio, often written CNR or ''C/N'', is the signal-to-noise ratio (SNR) of a modulated signal. The term is used to distinguish the CNR of the radio frequency passband signal from the SNR of an analog base band message signal after demodulation. For example, with FM radio, the strength of the 100 MHz carrier with modulations would be considered for CNR, whereas the audio frequency analogue message signal would be for SNR; in each case, compared to the apparent noise. If this distinction is not necessary, the term SNR is often used instead of CNR, with the same definition. Digitally modulated signals (e.g. QAM or PSK) are basically made of two CW carriers (the I and Q components, which are out-of-phase carriers). In fact, the information (bits or symbols) is carried by given combinations of phase and/or amplitude of the I and Q components. It is for this reason that, in the context of digital modulations, digitally modulated signals ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg "Click for more on -> Decibels")