|
Schwarz Minimal Surface
In differential geometry, the Schwarz minimal surfaces are periodic minimal surfaces originally described by Hermann Schwarz. In the 1880s Schwarz and his student E. R. Neovius described periodic minimal surfaces. They were later named by Alan Schoen in his seminal report that described the gyroid and other triply periodic minimal surfaces. The surfaces were generated using symmetry arguments: given a solution to Plateau's problem for a polygon, reflections of the surface across the boundary lines also produce valid minimal surfaces that can be continuously joined to the original solution. If a minimal surface meets a plane at right angles, then the mirror image in the plane can also be joined to the surface. Hence given a suitable initial polygon inscribed in a unit cell periodic surfaces can be constructed. The Schwarz surfaces have topological genus 3, the minimal genus of triply periodic minimal surfaces. They have been considered as models for periodic nanostr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Geometry
Differential geometry is a mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra. The field has its origins in the study of spherical geometry as far back as antiquity. It also relates to astronomy, the geodesy of the Earth, and later the study of hyperbolic geometry by Lobachevsky. The simplest examples of smooth spaces are the plane and space curves and surfaces in the three-dimensional Euclidean space, and the study of these shapes formed the basis for development of modern differential geometry during the 18th and 19th centuries. Since the late 19th century, differential geometry has grown into a field concerned more generally with geometric structures on differentiable manifolds. A geometric structure is one which defines some notion of size, distance, shape, volume, or other rigidifying str ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
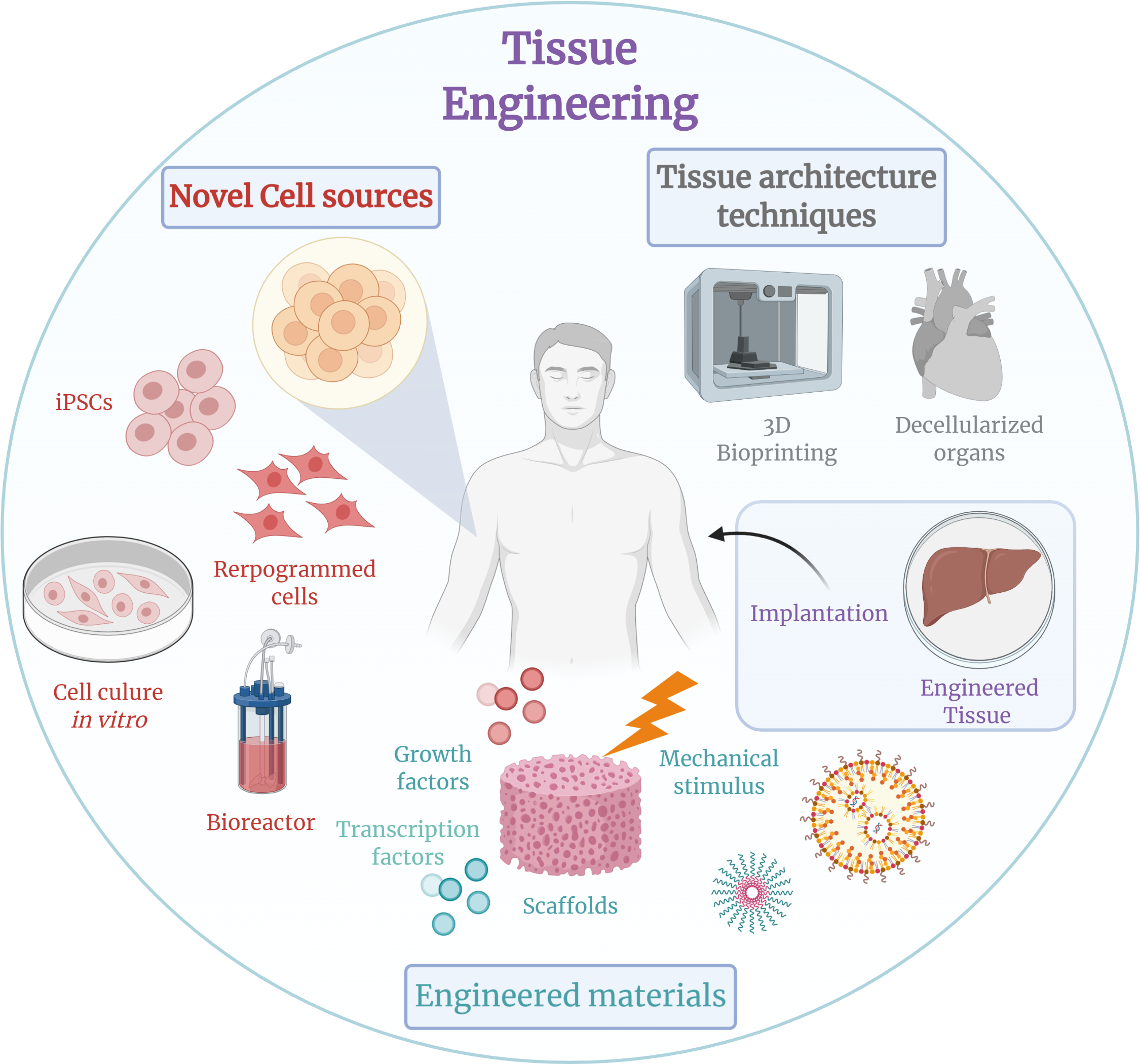
Tissue Engineering
Tissue engineering is a biomedical engineering discipline that uses a combination of cells, engineering, materials methods, and suitable biochemical and physicochemical factors to restore, maintain, improve, or replace different types of biological tissues. Tissue engineering often involves the use of cells placed on tissue scaffolds in the formation of new viable tissue for a medical purpose but is not limited to applications involving cells and tissue scaffolds. While it was once categorized as a sub-field of biomaterials, having grown in scope and importance it can be considered as a field of its own. While most definitions of tissue engineering cover a broad range of applications, in practice the term is closely associated with applications that repair or replace portions of or whole tissues (i.e. bone, cartilage, blood vessels, bladder, skin, muscle etc.). Often, the tissues involved require certain mechanical and structural properties for proper functioning. The term has al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schwarz CLP Surface
{{disambiguation ...
Schwarz may refer to: * Schwarz, Germany, a municipality in Mecklenburg-Vorpommern, Germany * Schwarz (surname), a surname (and list of people with the surname) * Schwarz (musician), American DJ and producer * ''Schwarz'' (Böhse Onkelz album), released simultaneously with ''Weiß'', 1993 * ''Schwarz'' (Conrad Schnitzler album), a reissue of the 1971 Kluster album ''Eruption'' * Schwarz (cards), in some card games, a Schneider (low point score) in which no tricks are taken * Schwarz Gruppe, a multinational retail group * Schwarz Pharma, a German drug company See also * * * Schwartz (other) * Schwarzhorn (other) * Swartz (other) Swartz may refer to: ;Places * Swartz, Louisiana *Swartz Creek (other) *Swartz Bay, British Columbia on the north end of the Saanich Peninsula on Vancouver Island ** Swartz Bay Ferry Terminal *Swartz Nunataks, in Antarctica ;People *Swart ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Catenoid
In geometry, a catenoid is a type of surface, arising by rotating a catenary curve about an axis (a surface of revolution). It is a minimal surface, meaning that it occupies the least area when bounded by a closed space. It was formally described in 1744 by the mathematician Leonhard Euler. Soap film attached to twin circular rings will take the shape of a catenoid. Because they are members of the same associate family of surfaces, a catenoid can be bent into a portion of a helicoid, and vice versa. Geometry The catenoid was the first non-trivial minimal surface in 3-dimensional Euclidean space to be discovered apart from the plane. The catenoid is obtained by rotating a catenary about its directrix. It was found and proved to be minimal by Leonhard Euler in 1744. Early work on the subject was published also by Jean Baptiste Meusnier. There are only two minimal surfaces of revolution ( surfaces of revolution which are also minimal surfaces): the plane and the catenoid. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schwarz H Surface
{{disambiguation ...
Schwarz may refer to: * Schwarz, Germany, a municipality in Mecklenburg-Vorpommern, Germany * Schwarz (surname), a surname (and list of people with the surname) * Schwarz (musician), American DJ and producer * ''Schwarz'' (Böhse Onkelz album), released simultaneously with ''Weiß'', 1993 * ''Schwarz'' (Conrad Schnitzler album), a reissue of the 1971 Kluster album ''Eruption'' * Schwarz (cards), in some card games, a Schneider (low point score) in which no tricks are taken * Schwarz Gruppe, a multinational retail group * Schwarz Pharma, a German drug company See also * * * Schwartz (other) * Schwarzhorn (other) * Swartz (other) Swartz may refer to: ;Places * Swartz, Louisiana * Swartz Creek (other) *Swartz Bay, British Columbia on the north end of the Saanich Peninsula on Vancouver Island **Swartz Bay Ferry Terminal * Swartz Nunataks, in Antarctica ;People * Swa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weierstrass Representation
Karl Theodor Wilhelm Weierstrass (german: link=no, Weierstraß ; 31 October 1815 – 19 February 1897) was a German mathematician often cited as the "father of modern analysis". Despite leaving university without a degree, he studied mathematics and trained as a school teacher, eventually teaching mathematics, physics, botany and gymnastics. He later received an honorary doctorate and became professor of mathematics in Berlin. Among many other contributions, Weierstrass formalized the definition of the continuity of a function, proved the intermediate value theorem and the Bolzano–Weierstrass theorem, and used the latter to study the properties of continuous functions on closed bounded intervals. Biography Weierstrass was born into a Roman Catholic family in Ostenfelde, a village near Ennigerloh, in the Province of Westphalia. Weierstrass was the son of Wilhelm Weierstrass, a government official, and Theodora Vonderforst both of whom were catholic Rhinelanders. His int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elliptic Integrals
In integral calculus, an elliptic integral is one of a number of related functions defined as the value of certain integrals, which were first studied by Giulio Fagnano and Leonhard Euler (). Their name originates from their originally arising in connection with the problem of finding the arc length of an ellipse. Modern mathematics defines an "elliptic integral" as any function which can be expressed in the form f(x) = \int_^ R \left(t, \sqrt \right) \, dt, where is a rational function of its two arguments, is a polynomial of degree 3 or 4 with no repeated roots, and is a constant. In general, integrals in this form cannot be expressed in terms of elementary functions. Exceptions to this general rule are when has repeated roots, or when contains no odd powers of or if the integral is pseudo-elliptic. However, with the appropriate reduction formula, every elliptic integral can be brought into a form that involves integrals over rational functions and the three Lege ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diamond Lattice
The diamond cubic crystal structure is a repeating pattern of 8 atoms that certain materials may adopt as they solidify. While the first known example was diamond, other elements in group 14 also adopt this structure, including α-tin, the semiconductors silicon and germanium, and silicon–germanium alloys in any proportion. There are also crystals, such as the high-temperature form of cristobalite, which have a similar structure, with one kind of atom (such as silicon in cristobalite) at the positions of carbon atoms in diamond but with another kind of atom (such as oxygen) halfway between those (see :Minerals in space group 227). Although often called the diamond lattice, this structure is not a lattice in the technical sense of this word used in mathematics. Crystallographic structure Diamond's cubic structure is in the Fdm space group (space group 227), which follows the face-centered cubic Bravais lattice. The lattice describes the repeat pattern; for diamond cubic c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schwarz D Surface
{{disambiguation ...
Schwarz may refer to: * Schwarz, Germany, a municipality in Mecklenburg-Vorpommern, Germany * Schwarz (surname), a surname (and list of people with the surname) * Schwarz (musician), American DJ and producer * ''Schwarz'' (Böhse Onkelz album), released simultaneously with ''Weiß'', 1993 * ''Schwarz'' (Conrad Schnitzler album), a reissue of the 1971 Kluster album ''Eruption'' * Schwarz (cards), in some card games, a Schneider (low point score) in which no tricks are taken * Schwarz Gruppe, a multinational retail group * Schwarz Pharma, a German drug company See also * * * Schwartz (other) * Schwarzhorn (other) * Swartz (other) Swartz may refer to: ;Places * Swartz, Louisiana *Swartz Creek (other) *Swartz Bay, British Columbia on the north end of the Saanich Peninsula on Vancouver Island ** Swartz Bay Ferry Terminal *Swartz Nunataks, in Antarctica ;People *Swart ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triply Periodic Minimal Surface
In differential geometry, a triply periodic minimal surface (TPMS) is a minimal surface in ℝ3 that is invariant under a rank-3 lattice of translations. These surfaces have the symmetries of a crystallographic group. Numerous examples are known with cubic, tetragonal, rhombohedral, and orthorhombic symmetries. Monoclinic and triclinic examples are certain to exist, but have proven hard to parametrise. TPMS are of relevance in natural science. TPMS have been observed as biological membranes, as block copolymers, equipotential surfaces in crystals etc. They have also been of interest in architecture, design and art. Properties Nearly all studied TPMS are free of self-intersections (i.e. embedded in ℝ3): from a mathematical standpoint they are the most interesting (since self-intersecting surfaces are trivially abundant). All connected TPMS have genus ≥ 3, and in every lattice there exist orientable embedded TPMS of every genus ≥3. Embedded TPMS are orientable and divi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Block Copolymer
In polymer chemistry, a copolymer is a polymer derived from more than one species of monomer. The polymerization of monomers into copolymers is called copolymerization. Copolymers obtained from the copolymerization of two monomer species are sometimes called ''bipolymers''. Those obtained from three and four monomers are called ''terpolymers'' and ''quaterpolymers'', respectively. Copolymers can be characterized by a variety of techniques such as Nuclear magnetic resonance spectroscopy, NMR spectroscopy and size-exclusion chromatography to determine the molecular size, weight, properties, and composition of the material. Commercial copolymers include acrylonitrile butadiene styrene (ABS), styrene/butadiene co-polymer (SBR), nitrile rubber, styrene-acrylonitrile, styrene-isoprene-styrene (SIS) and ethylene-vinyl acetate, all of which are formed by chain-growth polymerization. Another production mechanism is step-growth polymerization, which is used to produce the nylon-12/6/66 co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |