|
Runcination
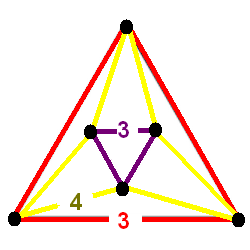
In geometry, runcination is an operation that cuts a regular polytope (or honeycomb) simultaneously along the faces, edges, and vertices, creating new facets in place of the original face, edge, and vertex centers. It is a higher order truncation operation, following cantellation, and truncation. It is represented by an extended Schläfli symbol t0,3. This operation only exists for 4-polytopes or higher. This operation is dual-symmetric for regular uniform 4-polytopes and 3-space convex uniform honeycombs. For a regular 4-polytope, the original cells remain, but become separated. The gaps at the separated faces become p-gonal prisms. The gaps between the separated edges become r-gonal prisms. The gaps between the separated vertices become cells. The vertex figure for a regular 4-polytope is an ''q''-gonal antiprism (called an ''antipodium'' if ''p'' and ''r'' are different). For regular 4-polytopes/honeycombs, this operation is also called expansion by Alicia Boole Stott ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform 4-polytope
In geometry, a uniform 4-polytope (or uniform polychoron) is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons. There are 47 non-prismatic convex uniform 4-polytopes. There are two infinite sets of convex prismatic forms, along with 17 cases arising as prisms of the convex uniform polyhedra. There are also an unknown number of non-convex star forms. History of discovery * Convex Regular polytopes: ** 1852: Ludwig Schläfli proved in his manuscript ''Theorie der vielfachen Kontinuität'' that there are exactly 6 regular polytopes in 4 dimensions and only 3 in 5 or more dimensions. * Regular star 4-polytopes (star polyhedron cells and/or vertex figures) ** 1852: Ludwig Schläfli also found 4 of the 10 regular star 4-polytopes, discounting 6 with cells or vertex figures and . ** 1883: Edmund Hess completed the list of 10 of the nonconvex regular 4-polytopes, in his book (in German) ''Einleitung in die Leh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated 120-cell
In four-dimensional geometry, a runcinated 120-cell (or ''runcinated 600-cell'') is a convex uniform 4-polytope, being a runcination (a 3rd order truncation) of the regular 120-cell. There are 4 degrees of runcinations of the 120-cell including with permutations truncations and cantellations. The ''runcinated 120-cell'' can be seen as an expansion applied to a regular 4-polytope, the 120-cell or 600-cell. Runcinated 120-cell The runcinated 120-cell or small disprismatohexacosihecatonicosachoron is a uniform 4-polytope. It has 2640 cells: 120 dodecahedra, 720 pentagonal prisms, 1200 triangular prisms, and 600 tetrahedra. Its vertex figure is a nonuniform triangular antiprism (equilateral-triangular antipodium): its bases represent a dodecahedron and a tetrahedron, and its flanks represent three triangular prisms and three pentagonal prisms. Alternate names * Runcinated 120-cell / Runcinated 600-cell (Norman W. Johnson) ** Runcinated hecatonicosachoron / Runcinated dodecacon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform 4-polytope
In geometry, a uniform 4-polytope (or uniform polychoron) is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons. There are 47 non-prismatic convex uniform 4-polytopes. There are two infinite sets of convex prismatic forms, along with 17 cases arising as prisms of the convex uniform polyhedra. There are also an unknown number of non-convex star forms. History of discovery * Convex Regular polytopes: ** 1852: Ludwig Schläfli proved in his manuscript ''Theorie der vielfachen Kontinuität'' that there are exactly 6 regular polytopes in 4 dimensions and only 3 in 5 or more dimensions. * Regular star 4-polytopes (star polyhedron cells and/or vertex figures) ** 1852: Ludwig Schläfli also found 4 of the 10 regular star 4-polytopes, discounting 6 with cells or vertex figures and . ** 1883: Edmund Hess completed the list of 10 of the nonconvex regular 4-polytopes, in his book (in German) ''Einleitung in die Leh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
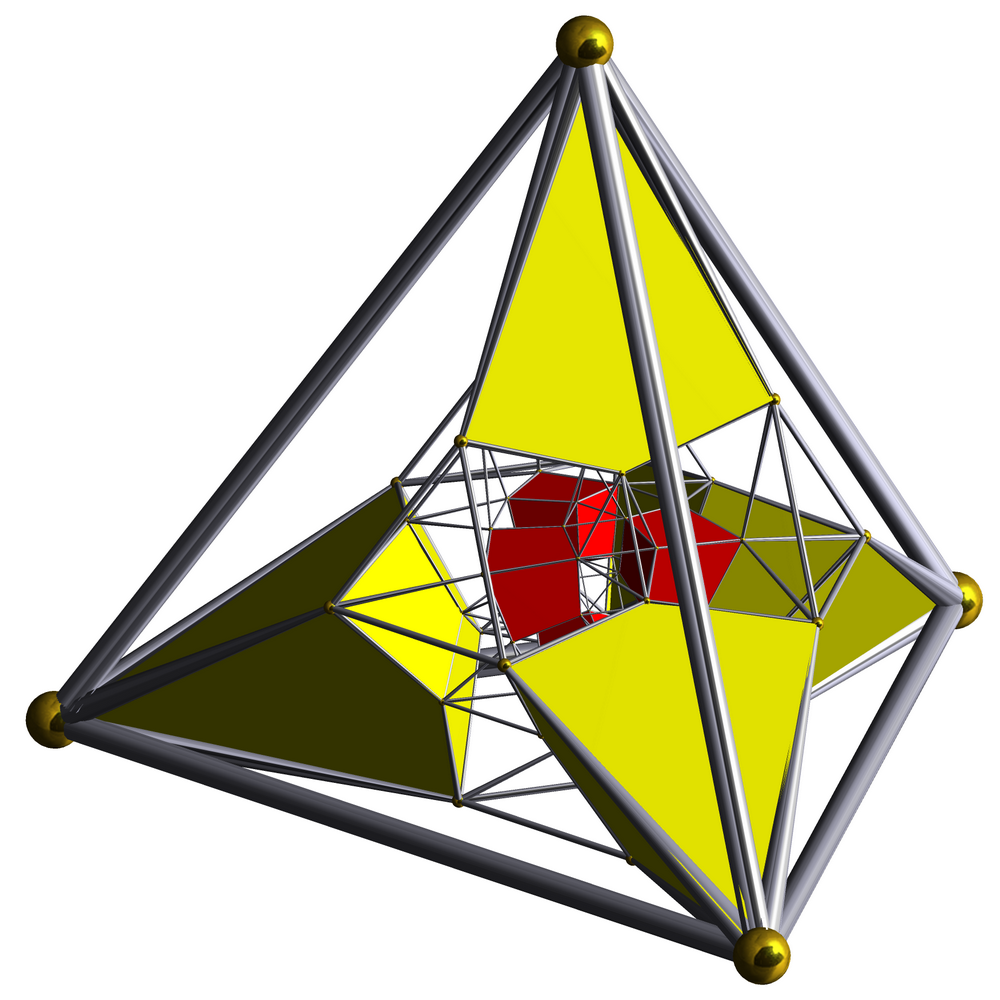
Runcinated 24-cell
In four-dimensional geometry, a runcinated 24-cell is a convex uniform 4-polytope, being a runcination (a 3rd order truncation) of the regular 24-cell. There are 3 unique degrees of runcinations of the 24-cell including with permutations truncations and cantellations. Runcinated 24-cell In geometry, the runcinated 24-cell or small prismatotetracontoctachoron is a uniform 4-polytope bounded by 48 octahedra and 192 triangular prisms. The octahedral cells correspond with the cells of a 24-cell and its dual. E. L. Elte identified it in 1912 as a semiregular polytope. Alternate names * Runcinated 24-cell ( Norman W. Johnson) * Runcinated icositetrachoron * Runcinated polyoctahedron * Small prismatotetracontoctachoron (spic) (Jonathan Bowers) Coordinates The Cartesian coordinates of the runcinated 24-cell having edge length 2 is given by all permutations of sign and coordinates of: : (0, 0, , 2+) : (1, 1, 1+, 1+) The permutations of the second set of coordinates coinc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated 16-cell
In four-dimensional geometry, a runcinated tesseract (or ''runcinated 16-cell'') is a convex uniform 4-polytope, being a runcination (a 3rd order truncation) of the regular tesseract. There are 4 variations of runcinations of the tesseract including with permutations truncations and cantellations. Runcinated tesseract The runcinated tesseract or (small) disprismatotesseractihexadecachoron has 16 tetrahedra, 32 cubes, and 32 triangular prisms. Each vertex is shared by 4 cubes, 3 triangular prisms and one tetrahedron. Construction The runcinated tesseract may be constructed by expanding the cells of a tesseract radially, and filling in the gaps with tetrahedra (vertex figures), cubes (face prisms), and triangular prisms (edge figure prisms). The same process applied to a 16-cell also yields the same figure. Cartesian coordinates The Cartesian coordinates of the vertices of the runcinated tesseract with edge length 2 are all permutations of: :\left(\pm 1,\ \pm 1,\ \pm 1,\ \p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
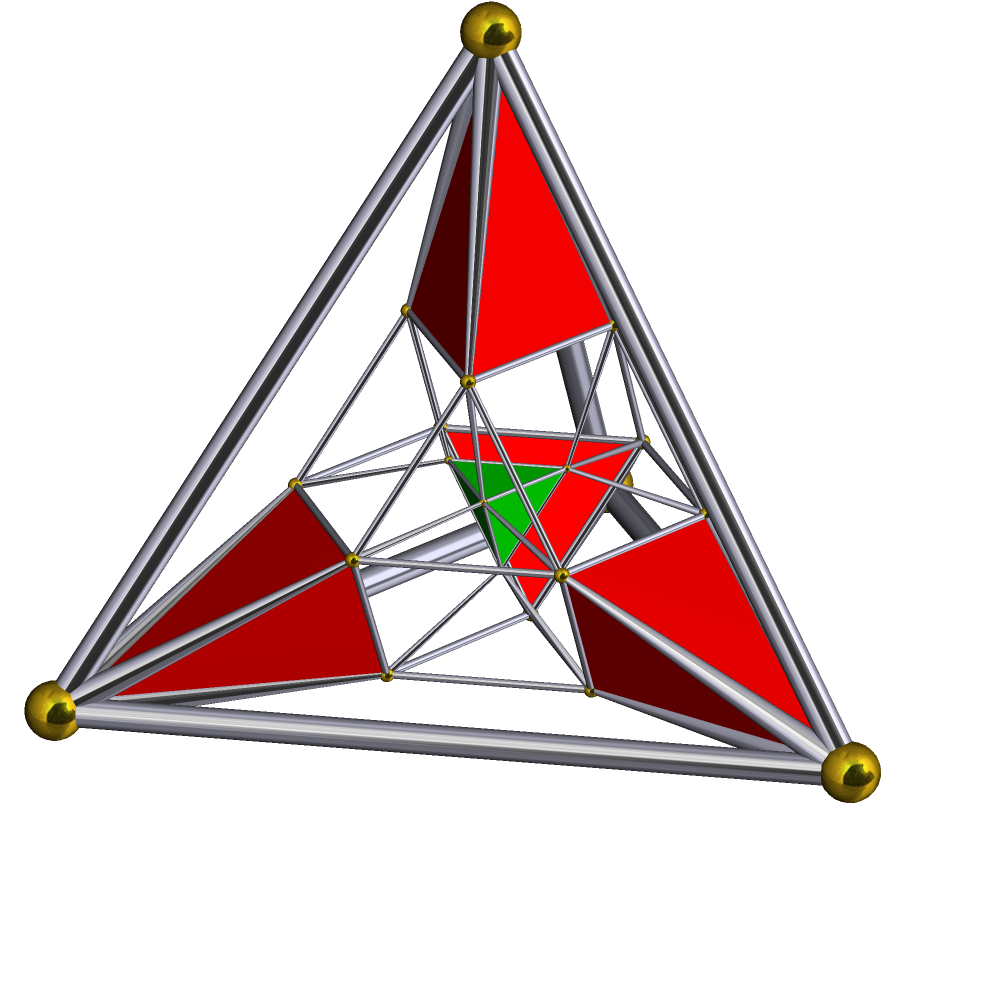
Runcinated 5-cell
In four-dimensional geometry, a runcinated 5-cell is a convex uniform 4-polytope, being a runcination (a 3rd order truncation, up to face-planing) of the regular 5-cell. There are 3 unique degrees of runcinations of the 5-cell, including with permutations, truncations, and cantellations. Runcinated 5-cell The runcinated 5-cell or small prismatodecachoron is constructed by expanding the cells of a 5-cell radially and filling in the gaps with triangular prisms (which are the face prisms and edge figures) and tetrahedra (cells of the dual 5-cell). It consists of 10 tetrahedra and 20 triangular prisms. The 10 tetrahedra correspond with the cells of a 5-cell and its dual. Topologically, under its highest symmetry, 3,3,3, there is only one geometrical form, containing 10 tetrahedra and 20 uniform triangular prisms. The rectangles are always squares because the two pairs of edges correspond to the edges of the two sets of 5 regular tetrahedra each in dual orientation, which are mad ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated 120-cell Verf
In geometry, runcination is an operation that cuts a regular polytope (or honeycomb) simultaneously along the faces, edges, and vertices, creating new facets in place of the original face, edge, and vertex centers. It is a higher order truncation operation, following cantellation, and truncation. It is represented by an extended Schläfli symbol t0,3. This operation only exists for 4-polytopes or higher. This operation is dual-symmetric for regular uniform 4-polytopes and 3-space convex uniform honeycombs. For a regular 4-polytope, the original cells remain, but become separated. The gaps at the separated faces become p-gonal prisms. The gaps between the separated edges become r-gonal prisms. The gaps between the separated vertices become cells. The vertex figure for a regular 4-polytope is an ''q''-gonal antiprism (called an ''antipodium'' if ''p'' and ''r'' are different). For regular 4-polytopes/honeycombs, this operation is also called expansion by Alicia Boole Stott ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated 24-cell Schlegel Halfsolid
In geometry, runcination is an operation that cuts a regular polytope (or honeycomb) simultaneously along the faces, edges, and vertices, creating new facets in place of the original face, edge, and vertex centers. It is a higher order truncation operation, following cantellation, and truncation. It is represented by an extended Schläfli symbol t0,3. This operation only exists for 4-polytopes or higher. This operation is dual-symmetric for regular uniform 4-polytopes and 3-space convex uniform honeycombs. For a regular 4-polytope, the original cells remain, but become separated. The gaps at the separated faces become p-gonal prisms. The gaps between the separated edges become r-gonal prisms. The gaps between the separated vertices become cells. The vertex figure for a regular 4-polytope is an ''q''-gonal antiprism (called an ''antipodium'' if ''p'' and ''r'' are different). For regular 4-polytopes/honeycombs, this operation is also called expansion by Alicia Boole Stott ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated 24-cell Verf
In geometry, runcination is an operation that cuts a regular polytope (or honeycomb) simultaneously along the faces, edges, and vertices, creating new facets in place of the original face, edge, and vertex centers. It is a higher order truncation operation, following cantellation, and truncation. It is represented by an extended Schläfli symbol t0,3. This operation only exists for 4-polytopes or higher. This operation is dual-symmetric for regular uniform 4-polytopes and 3-space convex uniform honeycombs. For a regular 4-polytope, the original cells remain, but become separated. The gaps at the separated faces become p-gonal prisms. The gaps between the separated edges become r-gonal prisms. The gaps between the separated vertices become cells. The vertex figure for a regular 4-polytope is an ''q''-gonal antiprism (called an ''antipodium'' if ''p'' and ''r'' are different). For regular 4-polytopes/honeycombs, this operation is also called expansion by Alicia Boole Stott ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated 8-cell Verf
In geometry, runcination is an operation that cuts a regular polytope (or honeycomb) simultaneously along the faces, edges, and vertices, creating new facets in place of the original face, edge, and vertex centers. It is a higher order truncation operation, following cantellation, and truncation. It is represented by an extended Schläfli symbol t0,3. This operation only exists for 4-polytopes or higher. This operation is dual-symmetric for regular uniform 4-polytopes and 3-space convex uniform honeycombs. For a regular 4-polytope, the original cells remain, but become separated. The gaps at the separated faces become p-gonal prisms. The gaps between the separated edges become r-gonal prisms. The gaps between the separated vertices become cells. The vertex figure for a regular 4-polytope is an ''q''-gonal antiprism (called an ''antipodium'' if ''p'' and ''r'' are different). For regular 4-polytopes/honeycombs, this operation is also called expansion by Alicia Boole Stott ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated 5-cell Verf
In geometry, runcination is an operation that cuts a regular polytope (or honeycomb) simultaneously along the faces, edges, and vertices, creating new facets in place of the original face, edge, and vertex centers. It is a higher order truncation operation, following cantellation, and truncation. It is represented by an extended Schläfli symbol t0,3. This operation only exists for 4-polytopes or higher. This operation is dual-symmetric for regular uniform 4-polytopes and 3-space convex uniform honeycombs. For a regular 4-polytope, the original cells remain, but become separated. The gaps at the separated faces become p-gonal prisms. The gaps between the separated edges become r-gonal prisms. The gaps between the separated vertices become cells. The vertex figure for a regular 4-polytope is an ''q''-gonal antiprism (called an ''antipodium'' if ''p'' and ''r'' are different). For regular 4-polytopes/honeycombs, this operation is also called expansion by Alicia Boole Sto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expansion (geometry)
In geometry, expansion is a polytope operation where facets are separated and moved radially apart, and new facets are formed at separated elements ( vertices, edges, etc.). Equivalently this operation can be imagined by keeping facets in the same position but reducing their size. The expansion of a regular polytope creates a uniform polytope, but the operation can be applied to any convex polytope, as demonstrated for polyhedra in Conway polyhedron notation (which represents expansion with the letter ). For polyhedra, an expanded polyhedron has all the faces of the original polyhedron, all the faces of the dual polyhedron, and new square faces in place of the original edges. Expansion of regular polytopes According to Coxeter, this multidimensional term was defined by Alicia Boole StottCoxeter, ''Regular Polytopes'' (1973), p. 123. p.210 for creating new polytopes, specifically starting from regular polytopes to construct new uniform polytopes. The ''expansion'' operation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |