|
Ross–Littlewood Paradox
The Ross–Littlewood paradox (also known as the balls and vase problem or the ping pong ball problem) is a hypothetical problem in abstract mathematics and Mathematical logic, logic designed to illustrate the paradoxical, or at least Intuition (knowledge), non-intuitive, nature of infinity. More specifically, like the Thomson's lamp paradox, the Ross–Littlewood paradox tries to illustrate the conceptual difficulties with the notion of a supertask, in which an infinite number of tasks are completed sequentially. The problem was originally described by mathematician John Edensor Littlewood, John E. Littlewood in his 1953 book ''Littlewood's Miscellany'', and was later expanded upon by Sheldon Ross in his 1988 book ''A First Course in Probability''. The problem starts with an empty vase and an infinite supply of balls. An infinite number of steps are then performed, such that at each step 10 balls are added to the vase and 1 ball removed from it. The question is then posed: ''How ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boole's Inequality
In probability theory, Boole's inequality, also known as the union bound, says that for any finite or countable set of events, the probability that at least one of the events happens is no greater than the sum of the probabilities of the individual events. This inequality provides an upper bound on the probability of occurrence of at least one of a countable number of events in terms of the individual probabilities of the events. Boole's inequality is named for its discoverer George Boole. Formally, for a countable set of events ''A''1, ''A''2, ''A''3, ..., we have :\left(\bigcup_^ A_i \right) \le \sum_^ (A_i). In measure-theoretic terms, Boole's inequality follows from the fact that a measure (and certainly any probability measure) is ''σ''- sub-additive. Proof Proof using induction Boole's inequality may be proved for finite collections of n events using the method of induction. For the n=1 case, it follows that :\mathbb P(A_1) \le \mathbb P(A_1). For the case n, we ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Victor Allis
Louis Victor Allis (born 19 May 1965) is a Dutch computer scientist working in the artificial intelligence (AI) field. In his graduate work, he revealed AI solutions for Connect Four, Qubic, and Gomoku. His dissertation introduced two new game search techniques: proof-number search and dependency-based search. Proof-number search has seen further successful application in computer Go tactical search and many other games. Career Allis holds a Ph.D. in Artificial Intelligence from Maastricht University, The Netherlands, and graduated ''cum laude'' with a M. Sc. in Computer Science from the Vrije Universiteit, The Netherlands. He has more than 30 publications to his name; the majority of his published work reports on research in search technologies. He started his career in 1987 as a freelance teacher, course developer and mentor of various AMBI courses for NOVI. Allis has lectured at the Vrije Universiteit in Amsterdam as an assistant professor in artificial intelligence. In 19 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Béla Bollobás
Béla Bollobás FRS (born 3 August 1943) is a Hungarian-born British mathematician who has worked in various areas of mathematics, including functional analysis, combinatorics, graph theory, and percolation. He was strongly influenced by Paul Erdős since the age of 14. Early life and education As a student, he took part in the first three International Mathematical Olympiads, winning two gold medals. Paul Erdős invited Bollobás to lunch after hearing about his victories, and they kept in touch afterward. Bollobás' first publication was a joint publication with ErdősBollobás, Béla; Erdös, Paul , Über graphentheoretische Extremalprobleme. (Extremal problems in graph theory.) , Mat. Lapok 13, 143-152 (1962) on extremal problems in graph theory, written when he was in high school in 1962. With Erdős's recommendation to Harold Davenport and a long struggle for permission from the Hungarian authorities, Bollobás was able to spend an undergraduate year in Cambridge, England ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert's Paradox Of The Grand Hotel
Hilbert's paradox of the Grand Hotel (colloquial: Infinite Hotel Paradox or Hilbert's Hotel) is a thought experiment which illustrates a counterintuitive property of infinite sets. It is demonstrated that a fully occupied hotel with infinitely many rooms may still accommodate additional guests, even infinitely many of them, and this process may be repeated infinitely often. The idea was introduced by David Hilbert in a 1924 lecture "Über das Unendliche", reprinted in , and was popularized through George Gamow's 1947 book '' One Two Three... Infinity''. The paradox Consider a hypothetical hotel with a countably infinite number of rooms, all of which are occupied. One might be tempted to think that the hotel would not be able to accommodate any newly arriving guests, as would be the case with a finite number of rooms, where the pigeonhole principle would apply. Finitely many new guests Suppose a new guest arrives and wishes to be accommodated in the hotel. We can (simultaneously) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
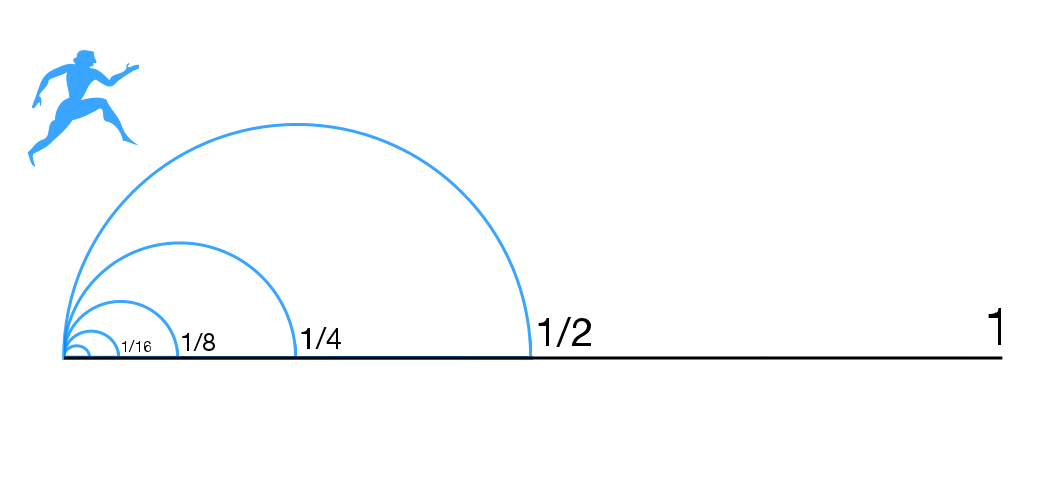
Supertask
In philosophy, a supertask is a countably infinite sequence of operations that occur sequentially within a finite interval of time. Supertasks are called hypertasks when the number of operations becomes uncountably infinite. A hypertask that includes one task for each ordinal number is called an ultratask. The term "supertask" was coined by the philosopher James F. Thomson, who devised Thomson's lamp. The term "hypertask" derives from Clark and Read in their paper of that name. History Zeno Motion The origin of the interest in supertasks is normally attributed to Zeno of Elea. Zeno claimed that motion was impossible. He argued as follows: suppose our burgeoning "mover", Achilles say, wishes to move from A to B. To achieve this he must traverse half the distance from A to B. To get from the midpoint of AB to B, Achilles must traverse half ''this'' distance, and so on and so forth. However many times he performs one of these "traversing" tasks, there is another one left for him t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jean Paul Van Bendegem
Jean Paul Van Bendegem (born 28 March 1953 in Ghent) is a mathematician, a philosopher of science, and a professor at the Vrije Universiteit Brussel in Brussels. Career Van Bendegem received his master's degree in mathematics in 1976. Afterwards, he went to study philosophy. He attended lectures on the philosophy of mathematics from Leo Apostel. He received his master's degree in philosophy in 1979. Van Bendegem wrote his PhD thesis in philosophy on the subject of finitism under the supervision of Diderik Batens while at Ghent University. He defended his thesis in 1983. The content of the thesis was on notation systems, number theory, analysis, physics and logic in a finite empirical framework. Van Bendegem was the dean of the faculty of Arts and philosophy, and was until his retirement in September 2018 head of the CLPS (Centre for Logic and Philosophy of Science) at the same university. He is an honorary chairman of SKEPP (Research Society for Critical Evaluation of Pseudosc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zeno's Paradoxes
Zeno's paradoxes are a set of philosophical problems generally thought to have been devised by Greek philosopher Zeno of Elea (c. 490–430 BC) to support Parmenides' doctrine that contrary to the evidence of one's senses, the belief in plurality and change is mistaken, and in particular that motion is nothing but an illusion. It is usually assumed, based on Plato's ''Parmenides'' (128a–d), that Zeno took on the project of creating these paradoxes because other philosophers had created paradoxes against Parmenides' view. Thus Plato has Zeno say the purpose of the paradoxes "is to show that their hypothesis that existences are many, if properly followed up, leads to still more absurd results than the hypothesis that they are one." Plato has Socrates claim that Zeno and Parmenides were essentially arguing exactly the same point. Some of Zeno's nine surviving paradoxes (preserved in Aristotle's ''Physics'' [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paul Benacerraf
Paul Joseph Salomon Benacerraf (; born 26 March 1931) is a French-born American philosopher working in the field of the philosophy of mathematics who taught at Princeton University his entire career, from 1960 until his retirement in 2007. He was appointed Stuart Professor of Philosophy in 1974, and retired as the James S. McDonnell Distinguished University Professor of Philosophy. Life and career Benacerraf was born in Paris to Moroccan Jewish parents. In 1939 the family moved to Caracas and then to New York City. When the family returned to Caracas, Benacerraf remained in the United States, boarding at the Peddie School in Hightstown, New Jersey. He attended Princeton University for both his undergraduate and graduate studies. He was elected a fellow of the American Academy of Arts and Sciences in 1998. His brother was the Venezuelan Nobel Prize-winning immunologist Baruj Benacerraf. Philosophical work Benacerraf is perhaps best known for his two papers "What Numbers Cou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit Superior And Limit Inferior
In mathematics, the limit inferior and limit superior of a sequence can be thought of as limiting (that is, eventual and extreme) bounds on the sequence. They can be thought of in a similar fashion for a function (see limit of a function). For a set, they are the infimum and supremum of the set's limit points, respectively. In general, when there are multiple objects around which a sequence, function, or set accumulates, the inferior and superior limits extract the smallest and largest of them; the type of object and the measure of size is context-dependent, but the notion of extreme limits is invariant. Limit inferior is also called infimum limit, limit infimum, liminf, inferior limit, lower limit, or inner limit; limit superior is also known as supremum limit, limit supremum, limsup, superior limit, upper limit, or outer limit. The limit inferior of a sequence x_n is denoted by \liminf_x_n\quad\text\quad \varliminf_x_n. The limit superior of a sequence x_n is denoted by \lims ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jim Henle
Jim or JIM may refer to: * Jim (given name), a given name * Jim, a diminutive form of the given name James * Jim, a short form of the given name Jimmy * OPCW-UN Joint Investigative Mechanism * ''Jim'' (comics), a series by Jim Woodring * ''Jim'' (album), by soul artist Jamie Lidell * Jim (''Huckleberry Finn''), a character in Mark Twain's novel * Jim (TV channel), in Finland * JIM (Flemish TV channel) * JIM suit, for atmospheric diving * Jim River, in North and South Dakota, United States * Jim, the nickname of Yelkanum Seclamatan (died April 1911), Native American chief * ''Journal of Internal Medicine'' * Juan Ignacio Martínez (born 1964), Spanish footballer, commonly known as JIM * Jim (horse), milk wagon horse used to produce serum containing diphtheria antitoxin * "Jim" (song), a 1941 song. * JIM, Jiangxi Isuzu Motors, a joint venture between Isuzu and Jiangling Motors Corporation Group (JMCG). * Jim (Medal of Honor recipient) See also * * Gym * Jjim * Ǧīm * Jam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tom Tymoczko
Tom or TOM may refer to: * Tom (given name), a diminutive of Thomas or Tomás or an independent Aramaic given name (and a list of people with the name) Characters * Tom Anderson, a character in ''Beavis and Butt-Head'' * Tom Beck, a character in the 1998 American science-fiction disaster movie '' Deep Impact'' * Tom Buchanan, the main antagonist from the 1925 novel ''The Great Gatsby'' * Tom Cat, a character from the ''Tom and Jerry'' cartoons * Tom Lucitor, a character from the American animated series ''Star vs. the Forces of Evil'' * Tom Natsworthy, from the science fantasy novel ''Mortal Engines'' * Tom Nook, a character in ''Animal Crossing'' video game series * Tom Servo, a robot character from the ''Mystery Science Theater 3000'' television series * Tom Sloane, a non-adult character from the animated sitcom ''Daria'' * Talking Tom, the protagonist from the ''Talking Tom & Friends'' franchise * Tom, a character from the '' Deltora Quest'' books by Emily Rodda * Tom, a cha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |