|
Romberg's Method
In numerical analysis, Romberg's method is used to estimate the definite integral \int_a^b f(x) \, dx by applying Richardson extrapolation repeatedly on the trapezium rule or the rectangle rule (midpoint rule). The estimates generate a triangular array. Romberg's method is a Newton–Cotes formula – it evaluates the integrand at equally spaced points. The integrand must have continuous derivatives, though fairly good results may be obtained if only a few derivatives exist. If it is possible to evaluate the integrand at unequally spaced points, then other methods such as Gaussian quadrature and Clenshaw–Curtis quadrature are generally more accurate. The method is named after Werner Romberg (1909–2003), who published the method in 1955. Method Using h_n = \frac, the method can be inductively defined by \begin R(0,0) &= h_1 (f(a) + f(b)) \\ R(n,0) &= \tfrac R(n-1,0) + h_n \sum_^ f(a + (2k-1)h_n) \\ R(n,m) &= R(n,m-1) + \tfrac (R(n,m-1) - R(n-1,m-1)) \\ &= \frac ( 4^m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods that attempt at finding approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics (predicting the motions of planets, stars and galaxies), numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living cells in medicine an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
One-piece Trapezoid Approximation
{{disambiguation ...
''One Piece'' is a Japanese manga franchise. One Piece, OnePiece, or one-piece may also refer to: * ''One Piece'' (TV series), a Japanese animated series based on the manga * ''One Piece'' (upcoming TV series), an upcoming Netflix live action series based on the manga * OnePiece (music production team), a South Korean music production team * One-piece swimsuit * One piece, a modern carbon fibre ice hockey stick See also * All in One (other) * Onesie (other) * Two-piece (other) * Three-piece (other) Three-piece may refer to: * Three-piece suit * Three-piece suite * Trio, three-piece band or act, a musical ensemble of three performers, for example as: ** Jazz trio ** Organ trio ** Piano trio ** Power trio ** String trio *Ronnie Lane or "Three- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MATLAB
MATLAB (an abbreviation of "MATrix LABoratory") is a proprietary multi-paradigm programming language and numeric computing environment developed by MathWorks. MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages. Although MATLAB is intended primarily for numeric computing, an optional toolbox uses the MuPAD symbolic engine allowing access to symbolic computing abilities. An additional package, Simulink, adds graphical multi-domain simulation and model-based design for dynamic and embedded systems. As of 2020, MATLAB has more than 4 million users worldwide. They come from various backgrounds of engineering, science, and economics. History Origins MATLAB was invented by mathematician and computer programmer Cleve Moler. The idea for MATLAB was based on his 1960s PhD thesis. Moler became a math professor at the University of New Mexico an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Springer-Verlag
Springer Science+Business Media, commonly known as Springer, is a German multinational publishing company of books, e-books and peer-reviewed journals in science, humanities, technical and medical (STM) publishing. Originally founded in 1842 in Berlin, it expanded internationally in the 1960s, and through mergers in the 1990s and a sale to venture capitalists it fused with Wolters Kluwer and eventually became part of Springer Nature in 2015. Springer has major offices in Berlin, Heidelberg, Dordrecht, and New York City. History Julius Springer founded Springer-Verlag in Berlin in 1842 and his son Ferdinand Springer grew it from a small firm of 4 employees into Germany's then second largest academic publisher with 65 staff in 1872.Chronology ". Springer Science+Business Media. In 1964, Springer expanded its business internationall ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
American Mathematical Society
The American Mathematical Society (AMS) is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, and serves the national and international community through its publications, meetings, advocacy and other programs. The society is one of the four parts of the Joint Policy Board for Mathematics and a member of the Conference Board of the Mathematical Sciences. History The AMS was founded in 1888 as the New York Mathematical Society, the brainchild of Thomas Fiske, who was impressed by the London Mathematical Society on a visit to England. John Howard Van Amringe was the first president and Fiske became secretary. The society soon decided to publish a journal, but ran into some resistance, due to concerns about competing with the American Journal of Mathematics. The result was the '' Bulletin of the American Mathematical Society'', with Fiske as editor-in-chief. The de facto journal, as intended, was influential ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Javascript (programming Language)
JavaScript (), often abbreviated as JS, is a programming language that is one of the core technologies of the World Wide Web, alongside HTML and CSS. As of 2022, 98% of Website, websites use JavaScript on the Client (computing), client side for Web page, webpage behavior, often incorporating third-party Library (computing), libraries. All major Web browser, web browsers have a dedicated JavaScript engine to execute the Source code, code on User (computing), users' devices. JavaScript is a High-level programming language, high-level, often Just-in-time compilation, just-in-time compiled language that conforms to the ECMAScript standard. It has dynamic typing, Prototype-based programming, prototype-based object-oriented programming, object-orientation, and first-class functions. It is Programming paradigm, multi-paradigm, supporting Event-driven programming, event-driven, functional programming, functional, and imperative programming, imperative programming paradigm, programmin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
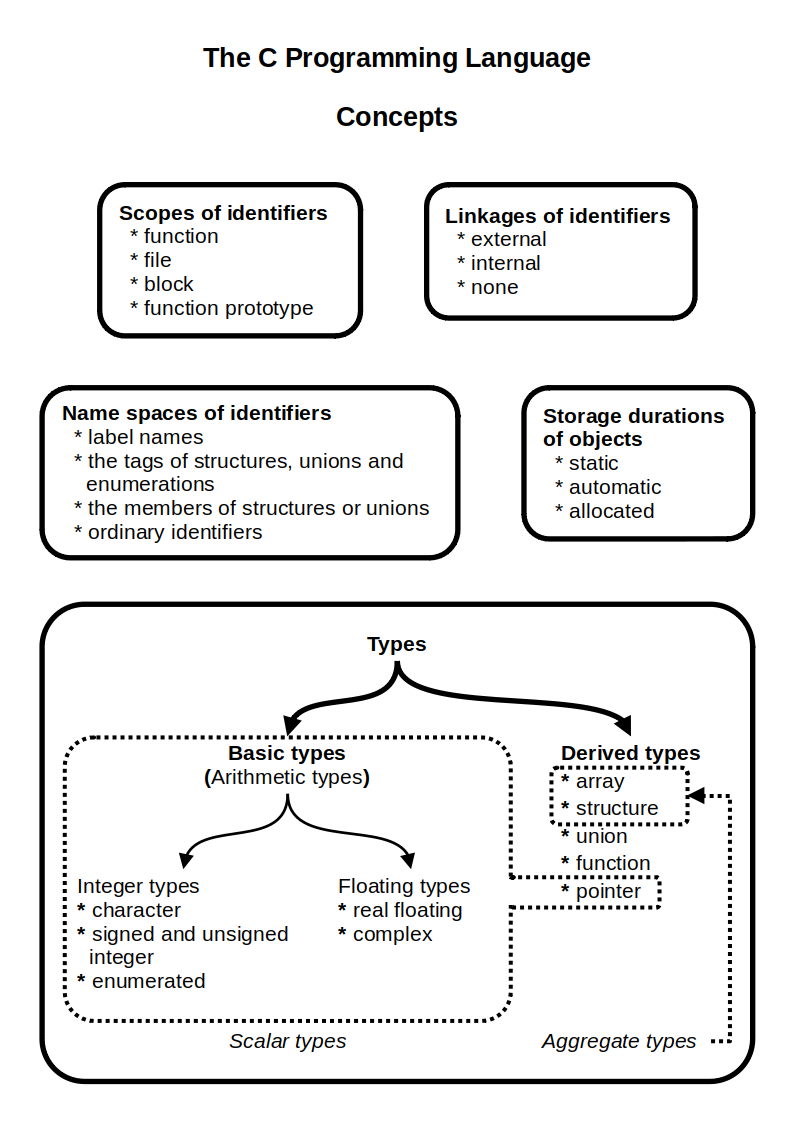
C (programming Language)
C (''pronounced like the letter c'') is a General-purpose language, general-purpose computer programming language. It was created in the 1970s by Dennis Ritchie, and remains very widely used and influential. By design, C's features cleanly reflect the capabilities of the targeted CPUs. It has found lasting use in operating systems, device drivers, protocol stacks, though decreasingly for application software. C is commonly used on computer architectures that range from the largest supercomputers to the smallest microcontrollers and embedded systems. A successor to the programming language B (programming language), B, C was originally developed at Bell Labs by Ritchie between 1972 and 1973 to construct utilities running on Unix. It was applied to re-implementing the kernel of the Unix operating system. During the 1980s, C gradually gained popularity. It has become one of the measuring programming language popularity, most widely used programming languages, with C compilers avail ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Error Function
In mathematics, the error function (also called the Gauss error function), often denoted by , is a complex function of a complex variable defined as: :\operatorname z = \frac\int_0^z e^\,\mathrm dt. This integral is a special (non- elementary) sigmoid function that occurs often in probability, statistics, and partial differential equations. In many of these applications, the function argument is a real number. If the function argument is real, then the function value is also real. In statistics, for non-negative values of , the error function has the following interpretation: for a random variable that is normally distributed with mean 0 and standard deviation , is the probability that falls in the range . Two closely related functions are the complementary error function () defined as :\operatorname z = 1 - \operatorname z, and the imaginary error function () defined as :\operatorname z = -i\operatorname iz, where is the imaginary unit Name The name "error functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Function
In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the base form f(x) = \exp (-x^2) and with parametric extension f(x) = a \exp\left( -\frac \right) for arbitrary real constants , and non-zero . It is named after the mathematician Carl Friedrich Gauss. The graph of a Gaussian is a characteristic symmetric " bell curve" shape. The parameter is the height of the curve's peak, is the position of the center of the peak, and (the standard deviation, sometimes called the Gaussian RMS width) controls the width of the "bell". Gaussian functions are often used to represent the probability density function of a normally distributed random variable with expected value and variance . In this case, the Gaussian is of the form g(x) = \frac \exp\left( -\frac \frac \right). Gaussian functions are widely used in statistics to describe the normal distributions, in signal processing to define Gaussian filters, in image processing where two-di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Four-piece Trapezoid Approximation
A musical ensemble, also known as a music group or musical group, is a group of people who perform instrumental and/or vocal music, with the ensemble typically known by a distinct name. Some music ensembles consist solely of instrumentalists, such as the jazz quartet or the orchestra. Other music ensembles consist solely of singers, such as choirs and doo wop groups. In both popular music and classical music, there are ensembles in which both instrumentalists and singers perform, such as the rock band or the Baroque chamber group for basso continuo (harpsichord and cello) and one or more singers. In classical music, trios or quartets either blend the sounds of musical instrument families (such as piano, strings, and wind instruments) or group together instruments from the same instrument family, such as string ensembles (e.g., string quartet) or wind ensembles (e.g., wind quintet). Some ensembles blend the sounds of a variety of instrument families, such as the orchestra, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Two-piece Trapezoid Approximation
Two-piece or Two piece or Two pieces may refer to: * Bikini, a two-piece swimsuit * Double act, a comedy duo * Two-piece band, a musical ensemble with two members, a duo * Two-piece gel encapsulation, a method of preparing a Capsule (pharmacy) containing a dose of medicine, invented in 1847 * Two piece implant, a form of Abutment (dentistry), a connecting element * Two-piece lapping, a version of the machining process Lapping * Two-piece sobralia ('' Sobralia dichotoma''), an orchid found in South America * Two-piece suit, a set of garments made from the same cloth; see Suit (clothing) * Two-piece tmRNAs, a type of Transfer-messenger RNA ; Music * "Two Pieces", a song on the record Demi (album) of 2013 by Demi Lovato (born 1992) * ''Two Pieces for Piano'' (1921), a composition by John Ireland (18791962) * ''Two Pieces for Piano'' (1925), a composition by John Ireland (18791962) * ''Two Pieces for Piano'' (1929-30), a composition by John Ireland (18791962) * Two Pieces for Wind ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
