|
Rock Mass Plasticity
300px, sinistral shear sense'', Starlight Pit, Fortnum Gold Mine, Western Australia Plasticity theory for rocks is concerned with the response of rocks to loads beyond the elastic limit. Historically, conventional wisdom has it that rock is brittle and fails by fracture while plasticity is identified with ductile materials. In field scale rock masses, structural discontinuities exist in the rock indicating that failure has taken place. Since the rock has not fallen apart, contrary to expectation of brittle behavior, clearly elasticity theory is not the last work.Pariseau (1988). Theoretically, the concept of rock plasticity is based on soil plasticity which is different from metal plasticity. In metal plasticity, for example in steel, the size of a dislocation is sub-grain size while for soil it is the relative movement of microscopic grains. The theory of soil plasticity was developed in the 1960s at Rice University to provide for inelastic effects not observed in metal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boudin Vein
Boudin () are various kinds of sausage in French, Luxembourgish, Belgian, Swiss, Québécois, Acadian, Aostan, Louisiana Creole, and Cajun cuisine. Etymology The Anglo-Norman word meant 'sausage', 'blood sausage' or 'entrails' in general. Its origin is unclear. It has been traced both to Romance and to Germanic roots, but there is not good evidence for either (cf. boudin. The English word "pudding" probably comes from . Types * '' ball'': A Cajun variation on . Instead of the filling being stuffed into pork casings, it is rolled into a ball, battered, and deep-fried. * : Originally, a white sausage made of pork without the blood. Variants include: ** French/Belgian boudin blanc, with milk. Generally sautéed or grilled. ** Cajun boudin blanc, made from a pork and rice mixture (much like dirty rice) in pork casings. Often includes pork liver and heart. Generally simmered or braised, although it may also be grilled. ** (): a traditional French , which may only conta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wedge Penetration
A wedge is a triangular shaped tool, and is a portable inclined plane, and one of the six simple machines. It can be used to separate two objects or portions of an object, lift up an object, or hold an object in place. It functions by converting a force applied to its blunt end into forces perpendicular ( normal) to its inclined surfaces. The mechanical advantage of a wedge is given by the ratio of the length of its slope to its width..''McGraw-Hill Concise Encyclopedia of Science & Technology'', Third Ed., Sybil P. Parker, ed., McGraw-Hill, Inc., 1992, p. 2041. Although a short wedge with a wide angle may do a job faster, it requires more force than a long wedge with a narrow angle. The force is applied on a flat, broad surface. This energy is transported to the pointy, sharp end of the wedge, hence the force is transported. The wedge simply transports energy in the form of friction and collects it to the pointy end, consequently breaking the item. History Wedges ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constitutive Model
In physics and engineering, a constitutive equation or constitutive relation is a relation between two physical quantities (especially kinetic quantities as related to kinematic quantities) that is specific to a material or substance, and approximates the response of that material to external stimuli, usually as applied fields or forces. They are combined with other equations governing physical laws to solve physical problems; for example in fluid mechanics the flow of a fluid in a pipe, in solid state physics the response of a crystal to an electric field, or in structural analysis, the connection between applied stresses or loads to strains or deformations. Some constitutive equations are simply phenomenological; others are derived from first principles. A common approximate constitutive equation frequently is expressed as a simple proportionality using a parameter taken to be a property of the material, such as electrical conductivity or a spring constant. However, it is of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boundary Condition
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional constraints, called the boundary conditions. A solution to a boundary value problem is a solution to the differential equation which also satisfies the boundary conditions. Boundary value problems arise in several branches of physics as any physical differential equation will have them. Problems involving the wave equation, such as the determination of normal modes, are often stated as boundary value problems. A large class of important boundary value problems are the Sturm–Liouville problems. The analysis of these problems involves the eigenfunctions of a differential operator. To be useful in applications, a boundary value problem should be well posed. This means that given the input to the problem there exists a unique solution, which depends continuously on the input. Much theoretical work in the field of partial differential eq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Initial Condition
In mathematics and particularly in dynamic systems, an initial condition, in some contexts called a seed value, is a value of an evolving variable at some point in time designated as the initial time (typically denoted ''t'' = 0). For a system of order ''k'' (the number of time lags in discrete time, or the order of the largest derivative in continuous time) and dimension ''n'' (that is, with ''n'' different evolving variables, which together can be denoted by an ''n''-dimensional coordinate vector), generally ''nk'' initial conditions are needed in order to trace the system's variables forward through time. In both differential equations in continuous time and difference equations in discrete time, initial conditions affect the value of the dynamic variables (state variables) at any future time. In continuous time, the problem of finding a closed form solution for the state variables as a function of time and of the initial conditions is called the initial value p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
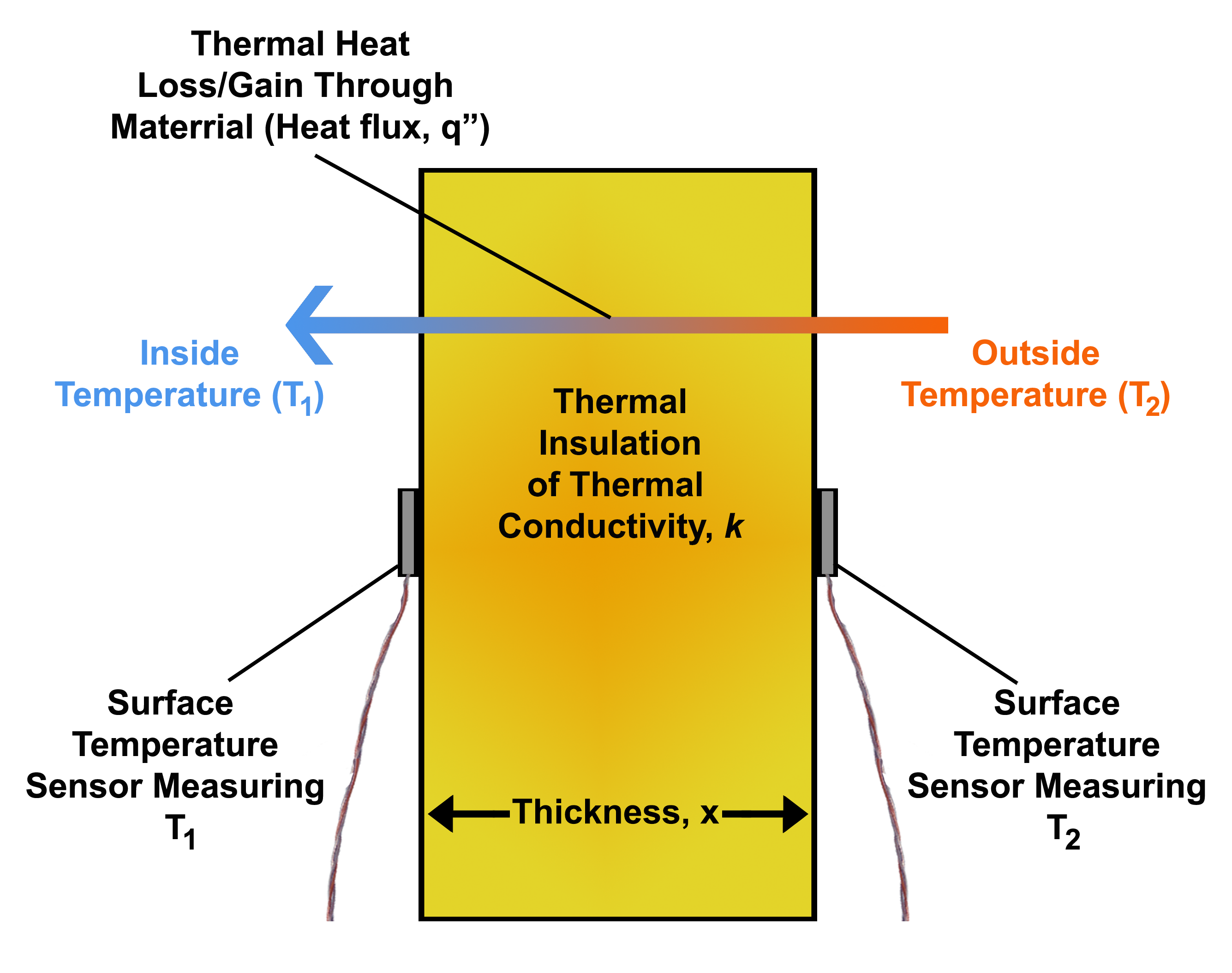
Heat Flux
Heat flux or thermal flux, sometimes also referred to as ''heat flux density'', heat-flow density or ''heat flow rate intensity'' is a flow of energy per unit area per unit time. In SI its units are watts per square metre (W/m2). It has both a direction and a magnitude, and so it is a vector quantity. To define the heat flux at a certain point in space, one takes the limiting case where the size of the surface becomes infinitesimally small. Heat flux is often denoted \vec_\mathrm, the subscript specifying ''heat'' flux, as opposed to ''mass'' or ''momentum'' flux. Fourier's law is an important application of these concepts. Fourier's law For most solids in usual conditions, heat is transported mainly by conduction and the heat flux is adequately described by Fourier's law. Fourier's law in one dimension \phi_\text = -k \frac where k is the thermal conductivity. The negative sign shows that heat flux moves from higher temperature regions to lower temperature regions. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Internal Energy
The internal energy of a thermodynamic system is the total energy contained within it. It is the energy necessary to create or prepare the system in its given internal state, and includes the contributions of potential energy and internal kinetic energy. It keeps account of the gains and losses of energy of the system that are due to changes in its internal state. It does not include the kinetic energy of motion of the system as a whole, or any external energies from surrounding force fields. The internal energy of an isolated system is constant, which is expressed as the law of conservation of energy, a foundation of the first law of thermodynamics. The internal energy is an extensive property. The internal energy cannot be measured directly and knowledge of all its components is rarely interesting, such as the static rest mass energy of its constituent matter. Thermodynamics is chiefly concerned only with ''changes'' in the internal energy, not with its absolute value. Instea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Body Force
In physics, a body force is a force that acts throughout the volume of a body. Springer site - Book 'Solid mechanics'preview paragraph 'Body forces'./ref> Forces due to gravity, electric fields and magnetic fields are examples of body forces. Body forces contrast with contact forces or surface forces which are exerted to the surface of an object. Normal forces and shear forces between objects are surface forces as they are exerted to the surface of an object. All cohesive surface attraction and contact forces between objects are also considered as surface forces. Fictitious forces such as the centrifugal force, Euler force, and the Coriolis effect are other examples of body forces. Definition Qualitative A body force is simply a type of force, and so it has the same dimensions as force, L] sup>−2. However, it is often convenient to talk about a body force in terms of either the force per unit volume or the force per unit mass. If the force per unit volume is of interest, i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy Stress Tensor
In continuum mechanics, the Cauchy stress tensor \boldsymbol\sigma, true stress tensor, or simply called the stress tensor is a second order tensor named after Augustin-Louis Cauchy. The tensor consists of nine components \sigma_ that completely define the state of stress at a point inside a material in the deformed state, placement, or configuration. The tensor relates a unit-length direction vector e to the traction vector T(e) across an imaginary surface perpendicular to e: :\mathbf^ = \mathbf e \cdot\boldsymbol\quad \text \quad T_^= \sigma_e_i, or, :\leftright\leftrightcdot \leftright The SI units of both stress tensor and traction vector are N/m2, corresponding to the stress scalar. The unit vector is dimensionless. The Cauchy stress tensor obeys the tensor transformation law under a change in the system of coordinates. A graphical representation of this transformation law is the Mohr's circle for stress. The Cauchy stress tensor is used for stress analysis of materi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Displacement (vector)
In geometry and mechanics, a displacement is a vector whose length is the shortest distance from the initial to the final position of a point P undergoing motion. It quantifies both the distance and direction of the net or total motion along a straight line from the initial position to the final position of the point trajectory. A displacement may be identified with the translation that maps the initial position to the final position. A displacement may be also described as a '' relative position'' (resulting from the motion), that is, as the final position of a point relative to its initial position . The corresponding displacement vector can be defined as the difference between the final and initial positions: s = x_\textrm - x_\textrm = \Delta In considering motions of objects over time, the instantaneous velocity of the object is the rate of change of the displacement as a function of time. The instantaneous speed, then, is distinct from velocity, or the time rate of chan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Velocity
Velocity is the directional speed of an object in motion as an indication of its rate of change in position as observed from a particular frame of reference and as measured by a particular standard of time (e.g. northbound). Velocity is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of bodies. Velocity is a physical vector quantity; both magnitude and direction are needed to define it. The scalar absolute value (magnitude) of velocity is called , being a coherent derived unit whose quantity is measured in the SI (metric system) as metres per second (m/s or m⋅s−1). For example, "5 metres per second" is a scalar, whereas "5 metres per second east" is a vector. If there is a change in speed, direction or both, then the object is said to be undergoing an ''acceleration''. Constant velocity vs acceleration To have a ''constant velocity'', an object must have a constant speed in a constant direction. Constant direction cons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Material Time Derivative
In continuum mechanics, the material derivative describes the time rate of change of some physical quantity (like heat or momentum) of a material element that is subjected to a space-and-time-dependent macroscopic velocity field. The material derivative can serve as a link between Eulerian and Lagrangian descriptions of continuum deformation. For example, in fluid dynamics, the velocity field is the flow velocity, and the quantity of interest might be the temperature of the fluid. In which case, the material derivative then describes the temperature change of a certain fluid parcel with time, as it flows along its pathline (trajectory). Other names There are many other names for the material derivative, including: *advective derivative *convective derivative *derivative following the motion *hydrodynamic derivative *Lagrangian derivative *particle derivative *substantial derivative *substantive derivative *Stokes derivative *total derivative, although the material derivative ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |