|
Regression Validation
In statistics, regression validation is the process of deciding whether the numerical results quantifying hypothesized relationships between variables, obtained from regression analysis, are acceptable as descriptions of the data. The validation process can involve analyzing the goodness of fit of the regression, analyzing whether the regression residuals are random, and checking whether the model's predictive performance deteriorates substantially when applied to data that were not used in model estimation. Goodness of fit One measure of goodness of fit is the ''R''2 (coefficient of determination), which in ordinary least squares with an intercept ranges between 0 and 1. However, an ''R''2 close to 1 does not guarantee that the model fits the data well: as Anscombe's quartet shows, a high ''R''2 can occur in the presence of misspecification of the functional form of a relationship or in the presence of outliers that distort the true relationship. One problem with the ''R''2 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Parameter
In statistics, as opposed to its general use in mathematics, a parameter is any measured quantity of a statistical population that summarises or describes an aspect of the population, such as a mean or a standard deviation. If a population exactly follows a known and defined distribution, for example the normal distribution, then a small set of parameters can be measured which completely describes the population, and can be considered to define a probability distribution for the purposes of extracting samples from this population. A parameter is to a population as a statistic is to a sample; that is to say, a parameter describes the ''true value'' calculated from the full population, whereas a statistic is an estimated measurement of the parameter based on a subsample. Thus a "statistical parameter" can be more specifically referred to as a population parameter..Everitt, B. S.; Skrondal, A. (2010), ''The Cambridge Dictionary of Statistics'', Cambridge University Press. Discuss ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Model Specification
In statistics, model specification is part of the process of building a statistical model: specification consists of selecting an appropriate functional form for the model and choosing which variables to include. For example, given personal income y together with years of schooling s and on-the-job experience x, we might specify a functional relationship y = f(s,x) as follows: : \ln y = \ln y_0 + \rho s + \beta_1 x + \beta_2 x^2 + \varepsilon where \varepsilon is the unexplained error term that is supposed to comprise independent and identically distributed Gaussian variables. The statistician Sir David Cox has said, "How hetranslation from subject-matter problem to statistical model is done is often the most critical part of an analysis". Specification error and bias Specification error occurs when the functional form or the choice of independent variables poorly represent relevant aspects of the true data-generating process. In particular, bias (the expected value of the di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Conclusion Validity
Statistical conclusion validity is the degree to which conclusions about the relationship among variables based on the data are correct or "reasonable". This began as being solely about whether the statistical conclusion about the relationship of the variables was correct, but now there is a movement towards moving to "reasonable" conclusions that use: quantitative, statistical, and qualitative data. Fundamentally, two types of errors can occur: type I (finding a difference or correlation when none exists) and type II (finding no difference or correlation when one exists). Statistical conclusion validity concerns the qualities of the study that make these types of errors more likely. Statistical conclusion validity involves ensuring the use of adequate sampling procedures, appropriate statistical tests, and reliable measurement procedures. Common threats The most common threats to statistical conclusion validity are: Low statistical power Power is the probability of correctly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Resampling (statistics)
In statistics, resampling is the creation of new samples based on one observed sample. Resampling methods are: # Permutation tests (also re-randomization tests) # Bootstrapping # Cross validation Permutation tests Permutation tests rely on resampling the original data assuming the null hypothesis. Based on the resampled data it can be concluded how likely the original data is to occur under the null hypothesis. Bootstrap Bootstrapping is a statistical method for estimating the sampling distribution of an estimator by sampling with replacement from the original sample, most often with the purpose of deriving robust estimates of standard errors and confidence intervals of a population parameter like a mean, median, proportion, odds ratio, correlation coefficient or regression coefficient. It has been called the plug-in principle,Logan, J. David and Wolesensky, Willian R. Mathematical methods in biology. Pure and Applied Mathematics: a Wiley-interscience Series of Texts, Mon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prediction Interval
In statistical inference, specifically predictive inference, a prediction interval is an estimate of an interval in which a future observation will fall, with a certain probability, given what has already been observed. Prediction intervals are often used in regression analysis. Prediction intervals are used in both frequentist statistics and Bayesian statistics: a prediction interval bears the same relationship to a future observation that a frequentist confidence interval or Bayesian credible interval bears to an unobservable population parameter: prediction intervals predict the distribution of individual future points, whereas confidence intervals and credible intervals of parameters predict the distribution of estimates of the true population mean or other quantity of interest that cannot be observed. Introduction For example, if one makes the parametric assumption that the underlying distribution is a normal distribution, and has a sample set , then confidence intervals ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
All Models Are Wrong
All or ALL may refer to: Language * All, an indefinite pronoun in English * All, one of the English determiners * Allar language (ISO 639-3 code) * Allative case (abbreviated ALL) Music * All (band), an American punk rock band * ''All'' (All album), 1999 * ''All'' (Descendents album) or the title song, 1987 * ''All'' (Horace Silver album) or the title song, 1972 * ''All'' (Yann Tiersen album), 2019 * "All" (song), by Patricia Bredin, representing the UK at Eurovision 1957 * "All (I Ever Want)", a song by Alexander Klaws, 2005 * "All", a song by Collective Soul from ''Hints Allegations and Things Left Unsaid'', 1994 Science and mathematics * ALL (complexity), the class of all decision problems in computability and complexity theory * Acute lymphoblastic leukemia * Anterolateral ligament Sports * American Lacrosse League * Arena Lacrosse League, Canada * Australian Lacrosse League Other uses * All, Missouri, a community in the United States * All, a brand of Sun Products * A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Squared Prediction Error
In statistics the mean squared prediction error or mean squared error of the predictions of a smoothing or curve fitting procedure is the expected value of the squared difference between the fitted values implied by the predictive function \widehat and the values of the (unobservable) function ''g''. It is an inverse measure of the explanatory power of \widehat, and can be used in the process of cross-validation of an estimated model. If the smoothing or fitting procedure has projection matrix (i.e., hat matrix) ''L'', which maps the observed values vector y to predicted values vector \hat via \hat=Ly, then :\operatorname(L)=\operatorname\left left( g(x_i)-\widehat(x_i)\right)^2\right The MSPE can be decomposed into two terms: the mean of squared biases of the fitted values and the mean of variances of the fitted values: :n\cdot\operatorname(L)=\sum_^n\left(\operatorname\left widehat(x_i)\rightg(x_i)\right)^2+\sum_^n\operatorname\left widehat(x_i)\right Knowledge of ''g'' is r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Squared Error
In statistics, the mean squared error (MSE) or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss. The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate. In machine learning, specifically empirical risk minimization, MSE may refer to the ''empirical'' risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution). The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
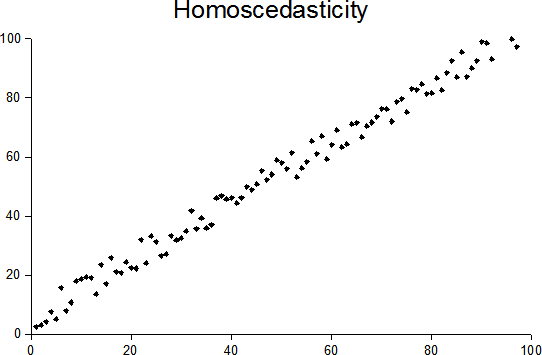
Heteroskedasticity
In statistics, a sequence (or a vector) of random variables is homoscedastic () if all its random variables have the same finite variance. This is also known as homogeneity of variance. The complementary notion is called heteroscedasticity. The spellings ''homoskedasticity'' and ''heteroskedasticity'' are also frequently used. Assuming a variable is homoscedastic when in reality it is heteroscedastic () results in unbiased but inefficient point estimates and in biased estimates of standard errors, and may result in overestimating the goodness of fit as measured by the Pearson coefficient. The existence of heteroscedasticity is a major concern in regression analysis and the analysis of variance, as it invalidates statistical tests of significance that assume that the modelling errors all have the same variance. While the ordinary least squares estimator is still unbiased in the presence of heteroscedasticity, it is inefficient and generalized least squares should be used ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Durbin–Watson Statistic
In statistics, the Durbin–Watson statistic is a test statistic used to detect the presence of autocorrelation at lag 1 in the residuals (prediction errors) from a regression analysis. It is named after James Durbin and Geoffrey Watson. The small sample distribution of this ratio was derived by John von Neumann (von Neumann, 1941). Durbin and Watson (1950, 1951) applied this statistic to the residuals from least squares regressions, and developed bounds tests for the null hypothesis that the errors are serially uncorrelated against the alternative that they follow a first order autoregressive process. Note that the distribution of this test statistic does not depend on the estimated regression coefficients and the variance of the errors. A similar assessment can be also carried out with the Breusch–Godfrey test and the Ljung–Box test. Computing and interpreting the Durbin–Watson statistic If ''et'' is the residual given by e_t = \rho e_+ \nu_t , the Durbin-Watson test ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Serial Correlation
Autocorrelation, sometimes known as serial correlation in the discrete time case, is the correlation of a signal with a delayed copy of itself as a function of delay. Informally, it is the similarity between observations of a random variable as a function of the time lag between them. The analysis of autocorrelation is a mathematical tool for finding repeating patterns, such as the presence of a periodic signal obscured by noise, or identifying the missing fundamental frequency in a signal implied by its harmonic frequencies. It is often used in signal processing for analyzing functions or series of values, such as time domain signals. Different fields of study define autocorrelation differently, and not all of these definitions are equivalent. In some fields, the term is used interchangeably with autocovariance. Unit root processes, trend-stationary processes, autoregressive processes, and moving average processes are specific forms of processes with autocorrelation. Auto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |