|
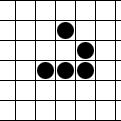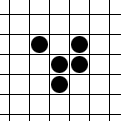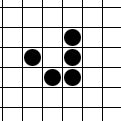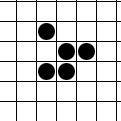
Reflector (cellular Automaton)
In cellular automata such as Conway's Game of Life, a reflector is a pattern that can interact with a spaceship to change its direction of motion, without damage to the reflector pattern. In Life, many oscillators can reflect the glider Glider may refer to: Aircraft and transport Aircraft * Glider (aircraft), heavier-than-air aircraft primarily intended for unpowered flight ** Glider (sailplane), a rigid-winged glider aircraft with an undercarriage, used in the sport of gliding ...; there also exist stable reflectors composed of still life patterns that, when they interact with a glider, reflect the glider and return to their stable state. External linksNew stable 180-degree glider reflector Game of Life News, May 30, 2009 Game of Life News, May 29, 2013 Cellular automaton patterns {{Comp-sci-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Color Coded Racetrack Large Channel
Color (American English) or colour (British English) is the visual perceptual property deriving from the spectrum of light interacting with the photoreceptor cells of the eyes. Color categories and physical specifications of color are associated with objects or materials based on their physical properties such as light absorption, reflection, or emission spectra. By defining a color space, colors can be identified numerically by their coordinates. Because perception of color stems from the varying spectral sensitivity of different types of cone cells in the retina to different parts of the spectrum, colors may be defined and quantified by the degree to which they stimulate these cells. These physical or physiological quantifications of color, however, do not fully explain the psychophysical perception of color appearance. Color science includes the perception of color by the eye and brain, the origin of color in materials, color theory in art, and the physics of electromagne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cellular Automaton
A cellular automaton (pl. cellular automata, abbrev. CA) is a discrete model of computation studied in automata theory. Cellular automata are also called cellular spaces, tessellation automata, homogeneous structures, cellular structures, tessellation structures, and iterative arrays. Cellular automata have found application in various areas, including physics, theoretical biology and microstructure modeling. A cellular automaton consists of a regular grid of ''cells'', each in one of a finite number of '' states'', such as ''on'' and ''off'' (in contrast to a coupled map lattice). The grid can be in any finite number of dimensions. For each cell, a set of cells called its ''neighborhood'' is defined relative to the specified cell. An initial state (time ''t'' = 0) is selected by assigning a state for each cell. A new ''generation'' is created (advancing ''t'' by 1), according to some fixed ''rule'' (generally, a mathematical function) that determines the new state ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conway's Game Of Life
The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970. It is a zero-player game, meaning that its evolution is determined by its initial state, requiring no further input. One interacts with the Game of Life by creating an initial configuration and observing how it evolves. It is Turing complete and can simulate a universal constructor or any other Turing machine. Rules The universe of the Game of Life is an infinite, two-dimensional orthogonal grid of square ''cells'', each of which is in one of two possible states, ''live'' or ''dead'' (or ''populated'' and ''unpopulated'', respectively). Every cell interacts with its eight ''neighbours'', which are the cells that are horizontally, vertically, or diagonally adjacent. At each step in time, the following transitions occur: # Any live cell with fewer than two live neighbours dies, as if by underpopulation. # Any live cell with two or three live ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spaceship (cellular Automaton)
In a cellular automaton, a finite pattern is called a spaceship if it reappears after a certain number of generations in the same orientation but in a different position. The smallest such number of generations is called the period of the spaceship. Description The speed of a spaceship is often expressed in terms of ''c'', the metaphorical speed of light (one cell per generation) which in many cellular automata is the fastest that an effect can spread. For example, a glider in Conway's Game of Life is said to have a speed of c/4, as it takes four generations for a given state to be translated by one cell. Similarly, the ''lightweight spaceship'' is said to have a speed of c/2, as it takes four generations for a given state to be translated by two cells. More generally, if a spaceship in a 2D automaton with the Moore neighborhood is translated by (x, y) after n generations, then the speed v is defined as: This notation can be readily generalised to cellular automata with di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oscillator (cellular Automaton)
In a cellular automaton, an oscillator is a pattern that returns to its original state, in the same orientation and position, after a finite number of generations. Thus the evolution of such a pattern repeats itself indefinitely. Depending on context, the term may also include spaceships as well. The smallest number of generations it takes before the pattern returns to its initial condition is called the ''period'' of the oscillator. An oscillator with a period of 1 is usually called a still life, as such a pattern never changes. Sometimes, still lifes are not taken to be oscillators. Another common stipulation is that an oscillator must be finite. Examples In Conway's Game of Life, finite oscillators are known to exist for all periods except 19 and 41. Additionally, until July 2022, the only known examples for period 34 were considered trivial because they consisted of essentially separate components that oscillate at smaller periods. For instance, one can create a period 34 osc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Glider (Conway's Life)
The glider is a pattern that travels across the board in Conway's Game of Life. It was first discovered by Richard K. Guy in 1969, while John Conway's group was attempting to track the evolution of the R-pentomino. Gliders are the smallest spaceships, and they travel diagonally at a speed of one cell every four generations, or c/4. The glider is often produced from randomly generated starting configurations. The name comes from the fact that, after two steps, the glider pattern repeats its configuration with a glide reflection symmetry. After four steps and two glide reflections, it returns to its original orientation. John Conway remarked that he wished he hadn't called it the glider. The game was developed before the widespread use of interactive computers, and after seeing it animated, he feels the glider looks more like an ant walking across the plane. Importance Gliders are important to the Game of Life because they are easily produced, can be collided with each other t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Still Life (cellular Automaton)
In Conway's Game of Life and other cellular automata, a still life is a pattern that does not change from one generation to the next. The term comes from the art world where a still life painting or photograph depicts an inanimate scene. In cellular automata, a still life can be thought of as an oscillator with unit period. Classification A pseudo still life consists of two or more adjacent islands ( connected components) which can be partitioned (either individually or as sets) into non-interacting subparts, which are also still lifes. This compares with a strict still life, which may not be partitioned in this way. A strict still life may have only a single island, or it may have multiple islands that depend on one another for stability, and thus cannot be decomposed. The distinction between the two is not always obvious, as a strict still life may have multiple connected components all of which are needed for its stability. However, it is possible to determine whether a still ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |