|
Range Query (data Structures)
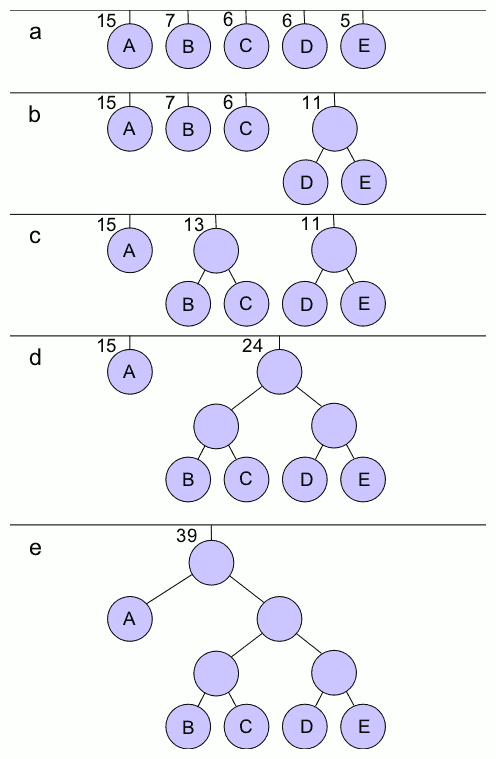
In computer science, the range query problem consists of efficiently answering several queries regarding a given interval of elements within an array. For example, a common task, known as range minimum query, is finding the smallest value inside a given range within a list of numbers. Definition Given a function f that accepts an array, a range query f_q(l, r) on an array a= _1,..,a_n/math> takes two indices l and r and returns the result of f when applied to the subarray _l, \ldots, a_r/math>. For example, for a function \operatorname that returns the sum of all values in an array, the range query \operatorname_q(l, r) returns the sum of all values in the range , r/math>. Solutions Prefix sum array Range sum queries may be answered in constant time and linear space by pre-computing an array of same length as the input such that for every index , the element is the sum of the first elements of . Any query may then be computed as follows: \operatorname_q(l, r) = p_r - ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Computer Science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, applied disciplines (including the design and implementation of Computer architecture, hardware and Software engineering, software). Algorithms and data structures are central to computer science. The theory of computation concerns abstract models of computation and general classes of computational problem, problems that can be solved using them. The fields of cryptography and computer security involve studying the means for secure communication and preventing security vulnerabilities. Computer graphics (computer science), Computer graphics and computational geometry address the generation of images. Programming language theory considers different ways to describe computational processes, and database theory concerns the management of re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Linear Time
In theoretical computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to be related by a constant factor. Since an algorithm's running time may vary among different inputs of the same size, one commonly considers the worst-case time complexity, which is the maximum amount of time required for inputs of a given size. Less common, and usually specified explicitly, is the average-case complexity, which is the average of the time taken on inputs of a given size (this makes sense because there are only a finite number of possible inputs of a given size). In both cases, the time complexity is gene ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Huffman Coding
In computer science and information theory, a Huffman code is a particular type of optimal prefix code that is commonly used for lossless data compression. The process of finding or using such a code is Huffman coding, an algorithm developed by David A. Huffman while he was a Doctor of Science, Sc.D. student at Massachusetts Institute of Technology, MIT, and published in the 1952 paper "A Method for the Construction of Minimum-Redundancy Codes". The output from Huffman's algorithm can be viewed as a variable-length code table for encoding a source symbol (such as a character in a file). The algorithm derives this table from the estimated probability or frequency of occurrence (''weight'') for each possible value of the source symbol. As in other entropy encoding methods, more common symbols are generally represented using fewer bits than less common symbols. Huffman's method can be efficiently implemented, finding a code in time linear time, linear to the number of input weigh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Range Tree
In computer science, a range tree is an ordered tree data structure, ordered tree data structure to hold a list of points. It allows all points within a given range to be Range query (computer science), reported efficiently, and is typically used in two or higher dimensions. Range trees were introduced by Jon Louis Bentley in 1979. Similar data structures were discovered independently by Lueker, Lee and Wong, and Willard. The range tree is an alternative to the k-d tree, ''k''-d tree. Compared to ''k''-d trees, range trees offer faster query times of (in Big O notation) O(\log^dn+k) but worse storage of O(n\log^ n), where ''n'' is the number of points stored in the tree, ''d'' is the dimension of each point and ''k'' is the number of points reported by a given query. In 1990, Bernard Chazelle improved this to query time O(\log^ n + k) and space complexity O\left(n\left(\frac\right)^\right). Data structure A range tree on a set of 1-dimensional points is a balanced binary sear ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Lowest Common Ancestor
In graph theory and computer science, the lowest common ancestor (LCA) (also called least common ancestor) of two nodes and in a Tree (graph theory), tree or directed acyclic graph (DAG) is the lowest (i.e. deepest) node that has both and as descendants, where we define each node to be a descendant of itself (so if has a direct connection from , is the lowest common ancestor). The LCA of and in is the shared ancestor of and that is located farthest from the root. Computation of lowest common ancestors may be useful, for instance, as part of a procedure for determining the distance between pairs of nodes in a tree: the distance from to can be computed as the distance from the root to , plus the distance from the root to , minus twice the distance from the root to their lowest common ancestor . In a tree data structure where each node points to its parent, the lowest common ancestor can be easily determined by finding the first intersection of the paths from and to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Boyer–Moore Majority Vote Algorithm
The Boyer–Moore majority vote algorithm is an algorithm for finding the majority of a sequence of elements using linear time and a constant number of words of memory. It is named after Robert S. Boyer and J Strother Moore, who published it in 1981,. Originally published as a technical report in 1981. and is a prototypical example of a streaming algorithm. In its simplest form, the algorithm finds a majority element, if there is one: that is, an element that occurs repeatedly for more than half of the elements of the input. A version of the algorithm that makes a second pass through the data can be used to verify that the element found in the first pass really is a majority. If a second pass is not performed and there is no majority, the algorithm will not detect that no majority exists. In the case that no strict majority exists, the returned element can be arbitrary; it is not guaranteed to be the element that occurs most often (the mode of the sequence). It is not possible fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Online Algorithm
In computer science, an online algorithm is one that can process its input piece-by-piece in a serial fashion, i.e., in the order that the input is fed to the algorithm, without having the entire input available from the start. In contrast, an offline algorithm is given the whole problem data from the beginning and is required to output an answer which solves the problem at hand. In operations research Operations research () (U.S. Air Force Specialty Code: Operations Analysis), often shortened to the initialism OR, is a branch of applied mathematics that deals with the development and application of analytical methods to improve management and ..., the area in which online algorithms are developed is called online optimization. As an example, consider the sorting algorithms selection sort and insertion sort: selection sort repeatedly selects the minimum element from the unsorted remainder and places it at the front, which requires access to the entire input; it is thus a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Fractional Cascading
In computer science, fractional cascading is a technique to speed up a sequence of binary searches for the same value in a sequence of related data structures. The first binary search in the sequence takes a logarithmic amount of time, as is standard for binary searches, but successive searches in the sequence are faster. The original version of fractional cascading, introduced in two papers by Chazelle and Guibas in 1986 (; ), combined the idea of cascading, originating in range searching data structures of and , with the idea of fractional sampling, which originated in . Later authors introduced more complex forms of fractional cascading that allow the data structure to be maintained as the data changes by a sequence of discrete insertion and deletion events. Example As a simple example of fractional cascading, consider the following problem. We are given as input a collection of k ordered lists L_i of numbers, such that the total length \sum_i , L_i, of all lists is n, and mus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Quickselect
In computer science, quickselect is a selection algorithm to find the ''k''th smallest element in an unordered list, also known as the ''k''th order statistic. Like the related quicksort sorting algorithm, it was developed by Tony Hoare, and thus is also known as Hoare's selection algorithm. Like quicksort, it is efficient in practice and has good average-case performance, but has poor worst-case performance. Quickselect and its variants are the selection algorithms most often used in efficient real-world implementations. Quickselect uses the same overall approach as quicksort, choosing one element as a pivot and partitioning the data in two based on the pivot, accordingly as less than or greater than the pivot. However, instead of recursing into both sides, as in quicksort, quickselect only recurses into one side – the side with the element it is searching for. This reduces the average complexity from O(n\log n) to O(n), with a worst case of O(n^2). As with quicksort, quic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Offline Algorithm
In computer science, an online algorithm is one that can process its input piece-by-piece in a serial fashion, i.e., in the order that the input is fed to the algorithm, without having the entire input available from the start. In contrast, an offline algorithm is given the whole problem data from the beginning and is required to output an answer which solves the problem at hand. In operations research, the area in which online algorithms are developed is called online optimization. As an example, consider the sorting algorithms selection sort and insertion sort: selection sort repeatedly selects the minimum element from the unsorted remainder and places it at the front, which requires access to the entire input; it is thus an offline algorithm. On the other hand, insertion sort considers one input element per iteration and produces a partial solution without considering future elements. Thus insertion sort is an online algorithm. Note that the final result of an insertion so ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Median Of Medians
In computer science, the median of medians is an approximate median selection algorithm, frequently used to supply a good pivot for an exact selection algorithm, most commonly quickselect, that selects the ''k''th smallest element of an initially unsorted array. Median of medians finds an approximate median in linear time. Using this approximate median as an improved pivot, the worst-case complexity of quickselect reduces from quadratic to ''linear'', which is also the asymptotically optimal worst-case complexity of any selection algorithm. In other words, the median of medians is an approximate median-selection algorithm that helps building an asymptotically optimal, exact general selection algorithm (especially in the sense of worst-case complexity), by producing good pivot elements. Median of medians can also be used as a pivot strategy in quicksort, yielding an optimal algorithm, with worst-case complexity O(n\log n). Although this approach optimizes the asymptotic worst-cas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Selection Problem
In computer science, a selection algorithm is an algorithm for finding the kth smallest value in a collection of ordered values, such as numbers. The value that it finds is called the order statistic. Selection includes as special cases the problems of finding the minimum, median, and maximum element in the collection. Selection algorithms include quickselect, and the median of medians algorithm. When applied to a collection of n values, these algorithms take linear time, O(n) as expressed using big O notation. For data that is already structured, faster algorithms may be possible; as an extreme case, selection in an already-sorted array takes Problem statement An algorithm for the selection problem takes as input a collection of values, and a It outputs the smallest of these values, or, in some versions of the problem, a collection of the k smallest values. For this to be well-defined, it should be possible to sort the values into an order from smallest to largest; for inst ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |