|
Ramanujan Sum
In number theory, Ramanujan's sum, usually denoted ''cq''(''n''), is a function of two positive integer variables ''q'' and ''n'' defined by the formula : c_q(n) = \sum_ e^, where (''a'', ''q'') = 1 means that ''a'' only takes on values coprime to ''q''. Srinivasa Ramanujan mentioned the sums in a 1918 paper. In addition to the expansions discussed in this article, Ramanujan's sums are used in the proof of Vinogradov's theorem that every sufficiently large odd number is the sum of three primes. Notation For integers ''a'' and ''b'', a\mid b is read "''a'' divides ''b''" and means that there is an integer ''c'' such that \frac b a = c. Similarly, a\nmid b is read "''a'' does not divide ''b''". The summation symbol :\sum_f(d) means that ''d'' goes through all the positive divisors of ''m'', e.g. :\sum_f(d) = f(1) + f(2) + f(3) + f(4) + f(6) + f(12). (a,\,b) is the greatest common divisor, \phi(n) is Euler's totient function, \mu(n) is the Möbius function, and \zeta(s) is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Number Theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic function, integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Mathematics is the queen of the sciences—and number theory is the queen of mathematics."German original: "Die Mathematik ist die Königin der Wissenschaften, und die Arithmetik ist die Königin der Mathematik." Number theorists study prime numbers as well as the properties of mathematical objects made out of integers (for example, rational numbers) or defined as generalizations of the integers (for example, algebraic integers). Integers can be considered either in themselves or as solutions to equations (Diophantine geometry). Questions in number theory are often best understood through the study of Complex analysis, analytical objects (for example, the Riemann zeta function) that encode properties of the integers, primes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Series (mathematics)
In mathematics, a series is, roughly speaking, a description of the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathematics, even for studying finite structures (such as in combinatorics) through generating functions. In addition to their ubiquity in mathematics, infinite series are also widely used in other quantitative disciplines such as physics, computer science, statistics and finance. For a long time, the idea that such a potentially infinite summation could produce a finite result was considered paradoxical. This paradox was resolved using the concept of a limit during the 17th century. Zeno's paradox of Achilles and the tortoise illustrates this counterintuitive property of infinite sums: Achilles runs after a tortoise, but when he reaches the position of the tortoise at the beginning of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press is the university press of the University of Cambridge. Granted letters patent by Henry VIII of England, King Henry VIII in 1534, it is the oldest university press A university press is an academic publishing house specializing in monographs and scholarly journals. Most are nonprofit organizations and an integral component of a large research university. They publish work that has been reviewed by schola ... in the world. It is also the King's Printer. Cambridge University Press is a department of the University of Cambridge and is both an academic and educational publisher. It became part of Cambridge University Press & Assessment, following a merger with Cambridge Assessment in 2021. With a global sales presence, publishing hubs, and offices in more than 40 Country, countries, it publishes over 50,000 titles by authors from over 100 countries. Its publishing includes more than 380 academic journals, monographs, reference works, school and uni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kloosterman Sum
In mathematics, a Kloosterman sum is a particular kind of exponential sum. They are named for the Dutch mathematician Hendrik Kloosterman, who introduced them in 1926 when he adapted the Hardy–Littlewood circle method to tackle a problem involving positive definite diagonal quadratic forms in four as opposed to five or more variables, which he had dealt with in his dissertation in 1924. Let be natural numbers. Then :K(a,b;m)=\sum_ e^. Here ''x*'' is the inverse of modulo . Context The Kloosterman sums are a finite ring analogue of Bessel functions. They occur (for example) in the Fourier expansion of modular forms. There are applications to mean values involving the Riemann zeta function, primes in short intervals, primes in arithmetic progressions, the spectral theory of automorphic functions and related topics. Properties of the Kloosterman sums *If or then the Kloosterman sum reduces to the Ramanujan sum. * depends only on the residue class of and modulo . Furtherm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Period
In mathematics, in the area of number theory, a Gaussian period is a certain kind of sum of roots of unity. The periods permit explicit calculations in cyclotomic fields connected with Galois theory and with harmonic analysis (discrete Fourier transform). They are basic in the classical theory called cyclotomy. Closely related is the Gauss sum, a type of exponential sum which is a linear combination of periods. History As the name suggests, the periods were introduced by Gauss and were the basis for his theory of compass and straightedge construction. For example, the construction of the heptadecagon (a formula that furthered his reputation) depended on the algebra of such periods, of which : 2 \cos \left(\frac\right) = \zeta + \zeta^ \, is an example involving the seventeenth root of unity : \zeta = \exp \left(\frac\right). General definition Given an integer ''n'' > 1, let ''H'' be any subgroup of the multiplicative group : G = (\mathbb/n\mathbb)^\times of invertible ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Number
A triangular number or triangle number counts objects arranged in an equilateral triangle. Triangular numbers are a type of figurate number, other examples being square numbers and cube numbers. The th triangular number is the number of dots in the triangular arrangement with dots on each side, and is equal to the sum of the natural numbers from 1 to . The sequence of triangular numbers, starting with the 0th triangular number, is (This sequence is included in the On-Line Encyclopedia of Integer Sequences .) Formula The triangular numbers are given by the following explicit formulas: T_n= \sum_^n k = 1+2+3+ \dotsb +n = \frac = , where \textstyle is a binomial coefficient. It represents the number of distinct pairs that can be selected from objects, and it is read aloud as " plus one choose two". The first equation can be illustrated using a visual proof. For every triangular number T_n, imagine a "half-square" arrangement of objects corresponding to the triangular numb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Number
In mathematics, a square number or perfect square is an integer that is the square (algebra), square of an integer; in other words, it is the multiplication, product of some integer with itself. For example, 9 is a square number, since it equals and can be written as . The usual notation for the square of a number is not the product , but the equivalent exponentiation , usually pronounced as " squared". The name ''square'' number comes from the name of the shape. The unit of area is defined as the area of a unit square (). Hence, a square with side length has area . If a square number is represented by ''n'' points, the points can be arranged in rows as a square each side of which has the same number of points as the square root of ''n''; thus, square numbers are a type of figurate numbers (other examples being Cube (algebra), cube numbers and triangular numbers). Square numbers are non-negative. A non-negative integer is a square number when its square root is again an intege ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Number Theorem
In mathematics, the prime number theorem (PNT) describes the asymptotic distribution of the prime numbers among the positive integers. It formalizes the intuitive idea that primes become less common as they become larger by precisely quantifying the rate at which this occurs. The theorem was proved independently by Jacques Hadamard and Charles Jean de la Vallée Poussin in 1896 using ideas introduced by Bernhard Riemann (in particular, the Riemann zeta function). The first such distribution found is , where is the prime-counting function (the number of primes less than or equal to ''N'') and is the natural logarithm of . This means that for large enough , the probability that a random integer not greater than is prime is very close to . Consequently, a random integer with at most digits (for large enough ) is about half as likely to be prime as a random integer with at most digits. For example, among the positive integers of at most 1000 digits, about one in 2300 is prime ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Von Mangoldt Function
In mathematics, the von Mangoldt function is an arithmetic function named after German mathematician Hans von Mangoldt. It is an example of an important arithmetic function that is neither multiplicative nor additive. Definition The von Mangoldt function, denoted by , is defined as :\Lambda(n) = \begin \log p & \textn=p^k \text p \text k \ge 1, \\ 0 & \text \end The values of for the first nine positive integers (i.e. natural numbers) are :0 , \log 2 , \log 3 , \log 2 , \log 5 , 0 , \log 7 , \log 2 , \log 3, which is related to . Properties The von Mangoldt function satisfies the identityApostol (1976) p.32Tenenbaum (1995) p.30 :\log(n) = \sum_ \Lambda(d). The sum is taken over all integers that divide . This is proved by the fundamental theorem of arithmetic, since the terms that are not powers of primes are equal to . For example, consider the case . Then :\begin \sum_ \Lambda(d) &= \Lambda(1) + \Lambda(2) + \Lambda(3) + \Lambda(4) + \Lambda(6) + \Lambda(12) \\ &= \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jordan's Totient Function
Let k be a positive integer. In number theory, the Jordan's totient function J_k(n) of a positive integer n equals the number of k-tuples of positive integers that are less than or equal to n and that together with n form a coprime set of k+1 integers. Jordan's totient function is a generalization of Euler's totient function, which is given by J_1(n). The function is named after Camille Jordan. Definition For each k, Jordan's totient function J_k is multiplicative and may be evaluated as :J_k(n)=n^k \prod_\left(1-\frac\right) \,, where p ranges through the prime divisors of n. Properties * \sum_ J_k(d) = n^k. \, :which may be written in the language of Dirichlet convolutions as :: J_k(n) \star 1 = n^k\, :and via Möbius inversion as ::J_k(n) = \mu(n) \star n^k. :Since the Dirichlet generating function of \mu is 1/\zeta(s) and the Dirichlet generating function of n^k is \zeta(s-k), the series for J_k becomes ::\sum_\frac = \frac. * An average order of J_k(n) is ::\frac. * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
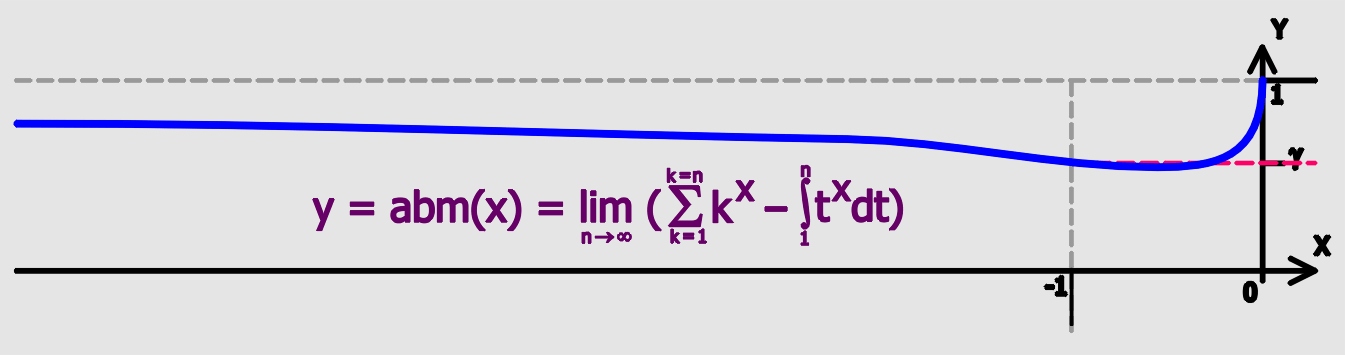
Euler–Mascheroni Constant
Euler's constant (sometimes also called the Euler–Mascheroni constant) is a mathematical constant usually denoted by the lowercase Greek letter gamma (). It is defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by \log: :\begin \gamma &= \lim_\left(-\log n + \sum_^n \frac1\right)\\ px&=\int_1^\infty\left(-\frac1x+\frac1\right)\,dx. \end Here, \lfloor x\rfloor represents the floor function. The numerical value of Euler's constant, to 50 decimal places, is: : History The constant first appeared in a 1734 paper by the Swiss mathematician Leonhard Euler, titled ''De Progressionibus harmonicis observationes'' (Eneström Index 43). Euler used the notations and for the constant. In 1790, Italian mathematician Lorenzo Mascheroni used the notations and for the constant. The notation appears nowhere in the writings of either Euler or Mascheroni, and was chosen at a later time perhaps because of the constant's connection ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann Hypothesis
In mathematics, the Riemann hypothesis is the conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . Many consider it to be the most important unsolved problem in pure mathematics. It is of great interest in number theory because it implies results about the distribution of prime numbers. It was proposed by , after whom it is named. The Riemann hypothesis and some of its generalizations, along with Goldbach's conjecture and the twin prime conjecture, make up Hilbert's eighth problem in David Hilbert's list of twenty-three unsolved problems; it is also one of the Clay Mathematics Institute's Millennium Prize Problems, which offers a million dollars to anyone who solves any of them. The name is also used for some closely related analogues, such as the Riemann hypothesis for curves over finite fields. The Riemann zeta function ζ(''s'') is a function whose argument ''s'' may be any complex number ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |